Integrale trigonometrischer Funktionen.
Beispiele für Lösungen

In dieser Lektion werden wir Integrale trigonometrischer Funktionen betrachten, das heißt, die Füllung der Integrale besteht aus Sinus, Cosinus, Tangens und Kotangens in verschiedenen Kombinationen. Alle Beispiele werden detailliert analysiert, zugänglich und auch für eine Teekanne verständlich.

Um Integrale trigonometrischer Funktionen erfolgreich zu studieren, müssen Sie die einfachsten Integrale gut verstehen und einige Integrationstechniken beherrschen. Diese Materialien können Sie in Vorlesungen kennenlernen Unbestimmtes Integral. Beispiele für Lösungen Und .

Und jetzt brauchen wir: Tabelle der Integrale, Derivatetabelle Und Verzeichnis trigonometrischer Formeln. Alle methodische Handbücher finden Sie auf der Seite Mathematische Formeln und Tabellen. Ich empfehle, alles auszudrucken. Mein besonderer Fokus liegt auf trigonometrischen Formeln, Sie sollten vor Ihren Augen sein– ohne dies wird die Arbeitseffizienz spürbar sinken.

Aber zuerst geht es in diesem Artikel darum, was Integrale sind NEIN. Es gibt keine Integrale der Form , - Kosinus, Sinus, multipliziert mit einem Polynom (seltener etwas mit Tangens oder Kotangens). Solche Integrale werden nach Teilen integriert. Um die Methode zu erlernen, besuchen Sie die Lektion Integration nach Teilen. Beispiele für Lösungen. Auch hier gibt es keine Integrale mit „Bögen“ – Arkustangens, Arkussinus usw., sie werden auch am häufigsten durch Teile integriert.

Beim Finden von Integralen trigonometrischer Funktionen werden verschiedene Methoden verwendet:

(4) Wir verwenden die tabellarische Formel , der einzige Unterschied besteht darin, dass wir anstelle von „X“ einen komplexen Ausdruck haben.

Beispiel 2

Beispiel 3

Finden Sie das unbestimmte Integral.

Ein Klassiker des Genres für diejenigen, die im Wettbewerb untergehen. Wie Sie wahrscheinlich bemerkt haben, gibt es in der Integraltabelle kein Integral von Tangens und Kotangens, aber dennoch können solche Integrale gefunden werden.

(1) Wir verwenden die trigonometrische Formel

(2) Wir bringen die Funktion unter das Differentialzeichen.

(3) Wir verwenden das Tabellenintegral .

Beispiel 4

Finden Sie das unbestimmte Integral.

Dies ist ein Beispiel für eine unabhängige Lösung. Die vollständige Lösung und Antwort finden Sie am Ende der Lektion.

Beispiel 5

Finden Sie das unbestimmte Integral.

Unsere Abschlüsse werden nach und nach steigen =).
Zuerst die Lösung:

(1) Wir verwenden die Formel

(2) Wir verwenden die trigonometrische Hauptidentität , woraus folgt .

(3) Teilen Sie den Zähler Term für Term durch den Nenner.

(4) Wir nutzen die Linearitätseigenschaft des unbestimmten Integrals.

(5) Wir integrieren mithilfe der Tabelle.

Beispiel 6

Finden Sie das unbestimmte Integral.

Dies ist ein Beispiel für eine unabhängige Lösung. Die vollständige Lösung und Antwort finden Sie am Ende der Lektion.

Es gibt auch Integrale von Tangenten und Kotangenten, die mehr sind hohe Abschlüsse. Das Integral des kubischen Tangens wird in der Lektion besprochen Wie berechnet man die Fläche einer flachen Figur? Integrale des Tangens (Kotangens) an die vierte und fünfte Potenz können auf der Seite ermittelt werden Komplexe Integrale.

Reduzierung des Integrandengrads

Diese Technik funktioniert, wenn die Integrandenfunktionen mit Sinus- und Cosinuswerten gefüllt sind sogar Grad. Um den Grad zu reduzieren, verwenden Sie trigonometrische Formeln , und , und die letzte Formel wird oft in die entgegengesetzte Richtung verwendet: .

Beispiel 7

Finden Sie das unbestimmte Integral.

Lösung:

Im Prinzip gibt es hier nichts Neues, außer dass wir die Formel angewendet haben (Erniedrigung des Integrandengrades). Bitte beachten Sie, dass ich die Lösung gekürzt habe. Mit zunehmender Erfahrung kann das Integral mündlich gefunden werden; das spart Zeit und ist bei der Erledigung von Aufgaben durchaus akzeptabel. In diesem Fall ist es ratsam, die Regel nicht zu beschreiben , zuerst bilden wir verbal das Integral von 1, dann von .

Beispiel 8

Finden Sie das unbestimmte Integral.

Dies ist ein Beispiel für eine unabhängige Lösung. Die vollständige Lösung und Antwort finden Sie am Ende der Lektion.

Das ist die versprochene Abschlusssteigerung:

Beispiel 9

Finden Sie das unbestimmte Integral.

Erst die Lösung, dann die Kommentare:

(1) Bereiten Sie den Integranden vor, um die Formel anzuwenden .

(2) Wir wenden die Formel tatsächlich an.

(3) Wir quadrieren den Nenner und entnehmen aus dem Integralzeichen die Konstante. Es hätte etwas anders gemacht werden können, aber meiner Meinung nach war es bequemer.

(4) Wir verwenden die Formel

(5) Im dritten Term reduzieren wir den Grad erneut, verwenden jedoch die Formel .

(6) Wir präsentieren ähnliche Begriffe(hier habe ich geteilt und machte die Addition).

(7) Eigentlich nehmen wir das Integral, die Linearitätsregel und die Methode zur Subsumierung einer Funktion unter dem Differentialzeichen wird mündlich durchgeführt.

(8) Kombination der Antwort.

! Bei einem unbestimmten Integral kann die Antwort oft auf verschiedene Arten geschrieben werden

In dem gerade betrachteten Beispiel hätte die endgültige Antwort anders geschrieben werden können – das Öffnen der Klammern und dies sogar vor der Integration des Ausdrucks, d. h. der folgende Abschluss des Beispiels ist durchaus akzeptabel:

Es ist durchaus möglich, dass diese Option noch bequemer ist, ich habe es nur so erklärt, wie ich es selbst gewohnt bin, es zu lösen. Hier ist ein weiteres typisches Beispiel für eine unabhängige Lösung:

Beispiel 10

Finden Sie das unbestimmte Integral.

Dieses Beispiel kann auf zwei Arten gelöst werden, und möglicherweise gelingt es Ihnen zwei völlig unterschiedliche Antworten(Genauer gesagt werden sie völlig anders aussehen, aber aus mathematischer Sicht sind sie gleichwertig). Höchstwahrscheinlich werden Sie nicht die rationalste Methode sehen und Probleme mit dem Öffnen von Klammern und der Verwendung anderer trigonometrischer Formeln haben. Die effektivste Lösung wird am Ende der Lektion angegeben.

Um den Absatz zusammenzufassen, schließen wir: jedes Integral der Form , wo und – sogar Zahlen, wird durch die Methode der Reduzierung des Integrandengrades gelöst.
In der Praxis stieß ich auf Integrale mit 8 und 10 Grad, und ich musste ihr schreckliches Durcheinander lösen, indem ich den Grad mehrmals verringerte, was zu langen, langen Antworten führte.

Variable Ersetzungsmethode

Wie im Artikel erwähnt Methode zur Variablenänderung im unbestimmten Integral Die Hauptvoraussetzung für die Verwendung der Ersetzungsmethode ist die Tatsache, dass es im Integranden eine bestimmte Funktion und deren Ableitung gibt:
(Funktionen sind nicht unbedingt im Produkt enthalten)

Beispiel 11

Finden Sie das unbestimmte Integral.

Wir schauen uns die Ableitungstabelle an und bemerken die Formeln, , das heißt, in unserem Integranden gibt es eine Funktion und ihre Ableitung. Wir sehen jedoch, dass sich bei der Differenzierung Kosinus und Sinus gegenseitig ineinander umwandeln, und es stellt sich die Frage: Wie führt man eine Änderung der Variablen durch und was verstehen wir unter Sinus oder Kosinus?! Die Frage lässt sich durch wissenschaftliche Forschung lösen: Wenn wir den Austausch falsch durchführen, wird nichts Gutes dabei herauskommen.

Eine allgemeine Richtlinie: In ähnlichen Fällen müssen Sie die Funktion angeben, die im Nenner steht.

Wir unterbrechen die Lösung und führen einen Ersatz durch

Im Nenner ist alles in Ordnung, alles hängt nur davon ab, jetzt bleibt abzuwarten, was daraus wird.
Dazu ermitteln wir das Differential:

Oder kurz gesagt:
Aus der resultierenden Gleichheit drücken wir unter Verwendung der Proportionsregel den Ausdruck aus, den wir benötigen:

Also:

Jetzt hängt unser gesamter Integrand nur noch davon ab und wir können mit der Lösung fortfahren

Bereit. Ich möchte Sie daran erinnern, dass der Zweck der Ersetzung darin besteht, den Integranden zu vereinfachen; in diesem Fall kam es darauf an, die Potenzfunktion gemäß der Tabelle zu integrieren.

Es ist kein Zufall, dass ich dieses Beispiel so ausführlich beschrieben habe; dies geschah zum Zweck der Wiederholung und Vertiefung des Unterrichtsstoffs Methode zur Variablenänderung im unbestimmten Integral.

Und nun zwei Beispiele für Ihre eigene Lösung:

Beispiel 12

Finden Sie das unbestimmte Integral.

Beispiel 13

Finden Sie das unbestimmte Integral.

Vollständige Lösungen und Antworten am Ende der Lektion.

Beispiel 14

Finden Sie das unbestimmte Integral.

Auch hier gibt es im Integranden Sinus und Cosinus (eine Funktion mit Ableitung), aber im Produkt entsteht ein Dilemma – was meinen wir mit Sinus oder Cosinus?

Sie können versuchen, einen Ersatz durch wissenschaftliches Stochern durchzuführen, und wenn nichts funktioniert, dann weisen Sie ihm eine andere Funktion zu, aber es gibt:

Allgemeine Richtlinie: Sie müssen die Funktion benennen, die sich im übertragenen Sinne in einer „unbequemen Position“ befindet..

Wir sehen, dass in diesem Beispiel der Studentenkosinus unter dem Grad „leidet“ und der Sinus frei und für sich allein sitzt.

Machen wir deshalb einen Ersatz:

Wenn jemand immer noch Schwierigkeiten mit dem Algorithmus zum Ersetzen einer Variablen und zum Finden des Differentials hat, sollten Sie zur Lektion zurückkehren Methode zur Variablenänderung im unbestimmten Integral.

Beispiel 15

Finden Sie das unbestimmte Integral.

Lassen Sie uns den Integranden analysieren. Was sollte mit bezeichnet werden?
Erinnern wir uns an unsere Richtlinien:
1) Die Funktion liegt höchstwahrscheinlich im Nenner;
2) Die Funktion befindet sich in einer „unbequemen Position“.

Diese Richtlinien gelten übrigens nicht nur für trigonometrische Funktionen.

Da der Sinus beide Kriterien erfüllt (insbesondere das zweite), liegt ein Austausch nahe. Im Prinzip kann der Austausch bereits durchgeführt werden, aber zunächst wäre es schön herauszufinden, was man damit machen soll? Zuerst „kneifen“ wir einen Kosinus ab:

Wir reservieren für unsere „zukünftige“ Differenzierung

Und wir drücken es durch den Hauptsinus aus trigonometrische Identität:

Hier nun der Ersatz:

Allgemeine Regel: Liegt im Integranden eine der trigonometrischen Funktionen (Sinus oder Cosinus) vor? seltsam Grad, dann müssen Sie eine Funktion vom ungeraden Grad „abbeißen“ und dahinter eine andere Funktion bezeichnen. Wir sprechen nur von Integralen, bei denen es Kosinus und Sinus gibt.

Im betrachteten Beispiel hatten wir einen Kosinus mit einer ungeraden Potenz, also haben wir einen Kosinus aus der Potenz genommen und ihn als Sinus bezeichnet.

Beispiel 16

Finden Sie das unbestimmte Integral.

Die Abschlüsse nehmen Fahrt auf =).
Dies ist ein Beispiel, das Sie selbst lösen können. Vollständige Lösung und Antwort am Ende der Lektion.

Universelle trigonometrische Substitution

Die universelle trigonometrische Substitution ist ein häufiger Fall der Variablenersetzungsmethode. Sie können versuchen, es zu verwenden, wenn Sie „nicht wissen, was Sie tun sollen“. Tatsächlich gibt es jedoch einige Richtlinien für die Anwendung. Typische Integrale, bei denen die universelle trigonometrische Substitution angewendet werden muss, sind die folgenden Integrale: , , , usw.

Beispiel 17

Finden Sie das unbestimmte Integral.

Die universelle trigonometrische Substitution wird in diesem Fall wie folgt implementiert. Machen wir einen Ersatz: . Ich verwende nicht den Buchstaben , aber der Buchstabe , das ist keine Regel, ich bin es nur gewohnt, Dinge auf diese Weise zu lösen.

Hier ist es bequemer, das Differential dafür zu finden, indem ich aus Gleichheit drücke:
Ich füge an beide Teile einen Arcustangens an:

Arkustangens und Tangens heben sich gegenseitig auf:

Daher:

In der Praxis muss man es gar nicht so ausführlich beschreiben, sondern nutzt einfach das fertige Ergebnis:

! Der Ausdruck ist nur gültig, wenn wir unter den Sinus- und Cosinuswerten einfach „X“ für das Integral haben (worüber wir später sprechen werden) Alles wird ein wenig anders sein!

Beim Ersetzen werden Sinus und Cosinus zu folgenden Brüchen:
, , diese Gleichungen basieren auf bekannten trigonometrischen Formeln: ,

Das endgültige Design könnte also so aussehen:

Führen wir eine universelle trigonometrische Substitution durch:

Es wird auch Probleme geben, die Sie selbst lösen müssen und auf die Sie die Antworten sehen können.

Der Integrand kann vom Produkt trigonometrischer Funktionen in die Summe umgewandelt werden

Betrachten wir Integrale, bei denen der Integrand das Produkt von Sinus und Cosinus ersten Grades von x multipliziert mit verschiedenen Faktoren ist, also Integrale der Form

Verwendung bekannter trigonometrischer Formeln

(2)
(3)
(4)
man kann jedes der Produkte in Integralen der Form (31) in eine algebraische Summe umwandeln und entsprechend den Formeln integrieren

(5)

(6)

Beispiel 1. Finden

Lösung. Nach Formel (2) bei

Beispiel 2. Finden Integral einer trigonometrischen Funktion

Lösung. Nach Formel (3) bei

Beispiel 3. Finden Integral einer trigonometrischen Funktion

Lösung. Nach Formel (4) bei wir erhalten die folgende Transformation des Integranden:

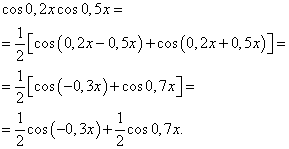
Wenn wir Formel (6) anwenden, erhalten wir

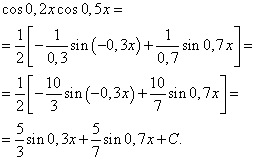
Integral des Produkts der Sinus- und Cosinuspotenzen desselben Arguments

Betrachten wir nun Integrale von Funktionen, die das Produkt von Sinus- und Cosinuspotenzen desselben Arguments sind, d. h.

(7)

In besonderen Fällen kann einer der Indikatoren ( M oder N) kann Null sein.

Bei der Integration solcher Funktionen wird davon ausgegangen, dass der gerade Grad des Kosinus durch den Sinus und der Differentialgrad des Sinus ausgedrückt werden kann gleich cos xdx(oder sogar die Potenz des Sinus kann als Kosinus ausgedrückt werden, und das Differential des Kosinus ist gleich - sin xdx ) .

Es sind zwei Fälle zu unterscheiden: 1) mindestens einer der Indikatoren M Und N seltsam; 2) Beide Indikatoren sind gerade.

Lassen Sie den ersten Fall eintreten, nämlich den Indikator N = 2k+ 1 - ungerade. Dann, wenn man das bedenkt

Der Integrand wird so dargestellt, dass ein Teil davon nur eine Funktion des Sinus ist und der andere Teil das Differential des Sinus ist. Verwenden Sie jetzt die Variablenersetzung T= Sünde X Die Lösung reduziert sich auf die Integration des Polynoms bezüglich T. Wenn nur der Abschluss M seltsam ist, dann machen sie dasselbe und isolieren den Faktor Sünde X, der den Rest des Integranden in Form von cos ausdrückt X und glauben T=cos X. Diese Technik kann auch verwendet werden, wenn Integration der Quotientenpotenzen von Sinus und Cosinus , Wann Mindestens einer der Indikatoren ist seltsam . Der springende Punkt ist das Der Quotient der Potenzen von Sinus und Cosinus ist ein Sonderfall ihres Produkts : Wenn eine trigonometrische Funktion im Nenner eines Integranden steht, ist ihr Grad negativ. Es gibt aber auch Fälle partieller trigonometrischer Funktionen, deren Potenzen nur gerade sind. Über sie - im nächsten Absatz.

Wenn beide Indikatoren M Und N– also sogar unter Verwendung trigonometrischer Formeln

Reduzieren Sie die Exponenten von Sinus und Cosinus, woraufhin ein Integral des gleichen Typs wie oben erhalten wird. Daher sollte die Integration nach dem gleichen Schema fortgesetzt werden. Wenn einer der geraden Exponenten negativ ist, also der Quotient gerader Potenzen von Sinus und Cosinus betrachtet wird, ist dieses Schema nicht geeignet . Dann wird eine Variablenänderung verwendet, je nachdem, wie der Integrand transformiert werden kann. Ein solcher Fall wird im nächsten Absatz behandelt.

Beispiel 4. Finden Integral einer trigonometrischen Funktion

Lösung. Der Kosinus-Exponent ist ungerade. Stellen wir uns daher vor

T= Sünde X(Dann dt=cos X dx ). Dann bekommen wir

Zurück zur alten Variablen finden wir endlich

Beispiel 5. Finden Integral einer trigonometrischen Funktion

.

Lösung. Der Kosinus-Exponent ist wie im vorherigen Beispiel ungerade, aber größer. Stellen wir uns vor

und nehmen Sie eine Änderung der Variablen vor T= Sünde X(Dann dt=cos X dx ). Dann bekommen wir

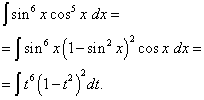
Öffnen wir die Klammern

und wir bekommen

Wenn wir zur alten Variablen zurückkehren, erhalten wir die Lösung

Beispiel 6. Finden Integral einer trigonometrischen Funktion

Lösung. Die Exponenten von Sinus und Cosinus sind gerade. Daher transformieren wir die Integrandenfunktion wie folgt:

Dann bekommen wir

Im zweiten Integral nehmen wir eine Änderung der Variablen Einstellung vor T= sin2 X. Dann (1/2)dt= cos2 X dx . Somit,

Endlich bekommen wir

Verwendung der Variablenersetzungsmethode

Variable Ersetzungsmethode Bei der Integration trigonometrischer Funktionen kann es in Fällen verwendet werden, in denen der Integrand nur Sinus oder nur Cosinus, das Produkt aus Sinus und Cosinus, bei dem entweder Sinus oder Cosinus im ersten Grad, Tangens oder Kotangens steht, sowie den Quotienten von enthält gerade Potenzen von Sinus und Cosinus ein und desselben Arguments. In diesem Fall ist es möglich, Permutationen durchzuführen, die nicht nur Sünde sind X = T und Sünde X = T, aber auch tg X = T und ctg X = T .

Beispiel 8. Finden Integral einer trigonometrischen Funktion

.

Lösung. Ändern wir die Variable: , then . Der resultierende Integrand kann mithilfe der Integraltabelle einfach integriert werden:

.

Beispiel 9. Finden Integral einer trigonometrischen Funktion

Lösung. Lassen Sie uns den Tangens in das Verhältnis von Sinus und Cosinus umwandeln:

Ändern wir die Variable: , then . Der resultierende Integrand ist Tabellenintegral mit Minuszeichen:

.

Zurück zur ursprünglichen Variablen erhalten wir schließlich:

.

Beispiel 10. Finden Integral einer trigonometrischen Funktion

Lösung. Ändern wir die Variable: , then .

Lassen Sie uns den Integranden transformieren, um die trigonometrische Identität anzuwenden :

Wir ändern die Variable und vergessen nicht, vor dem Integral ein Minuszeichen zu setzen (siehe oben, was gleich ist). dt). Als nächstes faktorisieren wir den Integranden und integrieren mithilfe der Tabelle:

Zurück zur ursprünglichen Variablen erhalten wir schließlich:

.

Finden Sie selbst das Integral einer trigonometrischen Funktion und schauen Sie sich dann die Lösung an

Universelle trigonometrische Substitution

Universelle trigonometrische Substitution kann in Fällen verwendet werden, in denen der Integrand nicht unter die in den vorherigen Absätzen diskutierten Fälle fällt. Grundsätzlich gilt, wenn Sinus oder Cosinus (oder beide) im Nenner eines Bruchs stehen. Es wurde nachgewiesen, dass Sinus und Cosinus wie folgt durch einen anderen Ausdruck ersetzt werden können, der den Tangens des halben ursprünglichen Winkels enthält:

Beachten Sie jedoch, dass die universelle trigonometrische Substitution oft recht komplexe algebraische Transformationen mit sich bringt, sodass sie am besten verwendet wird, wenn keine andere Methode funktioniert. Schauen wir uns Beispiele an, bei denen neben der universellen trigonometrischen Substitution auch die Substitution unter dem Differentialzeichen und die Methode der unbestimmten Koeffizienten verwendet werden.

Beispiel 12. Finden Integral einer trigonometrischen Funktion

.

Lösung. Lösung. Nutzen wir den Vorteil universelle trigonometrische Substitution. Dann
.

Wir multiplizieren die Brüche im Zähler und Nenner mit, nehmen die beiden heraus und stellen sie vor das Integralzeichen. Dann

Für Integration rationale Funktionen der Form R(sin x, cos x) wird eine Substitution verwendet, die als universelle trigonometrische Substitution bezeichnet wird. Dann . Die universelle trigonometrische Substitution führt häufig zu umfangreichen Berechnungen. Verwenden Sie daher, wann immer möglich, die folgenden Substitutionen.

Integration rational abhängiger Funktionen von trigonometrischen Funktionen

1. Integrale der Form ∫ sin n xdx , ∫ cos n xdx , n>0
a) Wenn n ungerade ist, sollte eine Potenz von sinx (oder cosx) unter dem Vorzeichen des Differentials eingegeben werden, und von der verbleibenden geraden Potenz sollte an die entgegengesetzte Funktion übergeben werden.
b) Wenn n gerade ist, verwenden wir Formeln zur Reduzierung des Grades
2. Integrale der Form ∫ tg n xdx , ∫ ctg n xdx , wobei n eine ganze Zahl ist.
Es müssen Formeln verwendet werden

3. Integrale der Form ∫ sin n x cos m x dx
a) Es seien m und n unterschiedliche Paritäten. Wir verwenden die Substitution t=sin x, wenn n ungerade ist, oder t=cos x, wenn m ungerade ist.
b) Wenn m und n gerade sind, verwenden wir Formeln zur Reduzierung des Grades
2sin 2 x=1-cos2x , 2cos 2 x=1+cos2x .
4. Integrale der Form
Wenn die Zahlen m und n die gleiche Parität haben, verwenden wir die Substitution t=tg x. Es ist oft praktisch, die Technik der trigonometrischen Einheit zu verwenden.
5. ∫ sin(nx) cos(mx)dx , ∫ cos(mx) cos(nx)dx , ∫ sin(mx) sin(nx)dx

Verwenden wir die Formeln zur Umrechnung des Produkts trigonometrischer Funktionen in ihre Summe:

• sin α cos β = ½(sin(α+β)+sin(α-β))
• cos α cos β = ½(cos(α+β)+cos(α-β))
• sin α sin β = ½(cos(α-β)-cos(α+β))

Beispiele
1. Berechnen Sie das Integral ∫ cos 4 x·sin 3 xdx .
Wir machen den Ersatz cos(x)=t. Dann ist ∫ cos 4 x sin 3 xdx =
2. Berechnen Sie das Integral.
Wenn wir die Ersetzung sin x=t durchführen, erhalten wir

3. Finden Sie das Integral.
Wir machen den Ersatz tg(x)=t . Wenn wir ersetzen, erhalten wir

Integrierende Ausdrücke der Form R(sinx, cosx)

Beispiel Nr. 1. Integrale berechnen:

Lösung.
a) Die Integration von Ausdrücken der Form R(sinx, cosx), wobei R eine rationale Funktion von sin x und cos x ist, wird mithilfe der universellen trigonometrischen Substitution tg(x/2) = t in Integrale rationaler Funktionen umgewandelt.
Dann haben wir

Eine universelle trigonometrische Substitution ermöglicht es, von einem Integral der Form ∫ R(sinx, cosx) dx zu einem Integral einer gebrochenen rationalen Funktion zu gelangen, aber oft führt eine solche Substitution zu umständlichen Ausdrücken. Unter bestimmten Voraussetzungen sind einfachere Substitutionen wirksam:

• Wenn die Gleichheit R(-sin x, cos x) = -R(sin x, cos x)dx erfüllt ist, dann wird die Substitution cos x = t angewendet.
• Wenn die Gleichheit R(sin x, -cos x) = -R(sin x, cos x)dx gilt, dann ist die Substitution sin x = t.
• Wenn die Gleichheit R(-sin x, -cos x) = R(sin x, cos x)dx gilt, dann ist die Substitution tgx = t oder ctg x = t.

In diesem Fall, um das Integral zu finden
Wenden wir die universelle trigonometrische Substitution tg(x/2) = t an.
Dann antworten Sie:

Im Detail werden Beispiele für partielle Integrallösungen betrachtet, deren Integrand das Produkt eines Polynoms mit einer Exponentialfunktion (e hoch x) oder mit einem Sinus (sin x) oder einem Kosinus (cos x) ist.

Inhalt

Siehe auch: Methode der partiellen Integration
Tabelle der unbestimmten Integrale
Methoden zur Berechnung unbestimmter Integrale
Grundlegende Elementarfunktionen und ihre Eigenschaften

Formel für die partielle Integration

Bei der Lösung der Beispiele in diesem Abschnitt wird die Formel für die partielle Integration verwendet:
;
.

Beispiele für Integrale, die das Produkt eines Polynoms und sin x, cos x oder e x enthalten

Hier sind Beispiele für solche Integrale:
, , .

Um solche Integrale zu integrieren, wird das Polynom mit u und der verbleibende Teil mit v dx bezeichnet.

Als nächstes wenden Sie die Formel für die partielle Integration an. Unten ist angegeben detaillierte Lösung

diese Beispiele.

Beispiele für die Lösung von Integralen

Beispiel mit Exponent, e hoch x
.

Bestimmen Sie das Integral:
Führen wir den Exponenten unter dem Differentialzeichen ein:.

e - x dx = - e - x d(-x) = - d(e - x)

Lassen Sie uns nach Teilen integrieren.
.
Hier
.
.
.
Wir integrieren auch das verbleibende Integral nach Teilen.
.

Endlich haben wir:

Ein Beispiel für die Definition eines Integrals mit Sinus
.

Berechnen Sie das Integral:

e - x dx = - e - x d(-x) = - d(e - x)

Lassen Sie uns den Sinus unter dem Differentialzeichen einführen: hier u = x 2 , v = cos(2 x+3) ( , du = )′ x 2

dx


Wir integrieren auch das verbleibende Integral nach Teilen. Führen Sie dazu den Kosinus unter dem Differentialzeichen ein. hier u = x, v = Sünde(2 x+3)

Wir integrieren auch das verbleibende Integral nach Teilen.

, du = dx

Ein Beispiel für die Definition eines Integrals mit Sinus
.

Beispiel für das Produkt eines Polynoms und eines Kosinus

e - x dx = - e - x d(-x) = - d(e - x)

hier u = x 2 + 3 x + 5, v = Sünde 2 x cos(2 x+3) ( x 2 + 3 x + 5 )′ x 2

Grundlegende trigonometrische Formeln und grundlegende Substitutionen werden vorgestellt. Methoden zur Integration trigonometrischer Funktionen werden skizziert - Integration rationaler Funktionen, Produkt Potenzfunktionen aus sin x und cos x, Produkt eines Polynoms, Exponentials und Sinus oder Cosinus, Integration inverser trigonometrischer Funktionen. Betroffen sind nicht standardmäßige Methoden.

Inhalt

Standardmethoden zur Integration trigonometrischer Funktionen

Allgemeiner Ansatz

Zunächst muss ggf. der Integrand so transformiert werden, dass die trigonometrischen Funktionen von einem einzigen Argument abhängen, das mit der Integrationsvariablen identisch ist.

Wenn zum Beispiel der Integrand abhängt von Sünde(x+a) Und cos(x+b), dann sollten Sie die Konvertierung durchführen:
cos (x+b) = cos (x+a - (a-b)) = cos (x+a) cos (b-a) + Sünde (x+a) Sünde (b-a).
Nehmen Sie dann die Ersetzung z = x+a vor.

Infolgedessen hängen trigonometrische Funktionen nur von der Integrationsvariablen z ab. Wenn trigonometrische Funktionen von einem Argument abhängen, das mit der Integrationsvariablen übereinstimmt (sagen wir, es ist z), besteht der Integrand also nur aus Funktionen wie, Sünde z, weil z, tg z ctg z
.
, dann müssen Sie eine Substitution vornehmen Diese Substitution führt zur Integration rationaler oder irrationaler Funktionen (sofern Wurzeln vorhanden sind) und ermöglicht die Berechnung des Integrals, wenn es integriert wird.

Elementarfunktionen

Allerdings gibt es oft auch andere Methoden, mit denen Sie das Integral auf kürzere Weise auf der Grundlage der Besonderheiten des Integranden auswerten können. Nachfolgend finden Sie eine Zusammenfassung der wichtigsten Methoden dieser Art.

Methoden zur Integration rationaler Funktionen von sin x und cos x Rationale Funktionen von Und Sünde x weil x Rationale Funktionen von, Sünde x sind Funktionen, die aus gebildet werden und alle Konstanten, die die Operationen Addition, Subtraktion, Multiplikation, Division und Potenzierung verwenden. Sie werden wie folgt bezeichnet: R(sin x, cos x)
.
.

Dazu können auch Tangens und Kotangens gehören, da sie durch Division von Sinus durch Cosinus und umgekehrt gebildet werden.
Integrale rationaler Funktionen haben die Form:
Methoden zur Integration rationaler trigonometrischer Funktionen sind wie folgt. und alle Konstanten, die die Operationen Addition, Subtraktion, Multiplikation, Division und Potenzierung verwenden. Sie werden wie folgt bezeichnet: R 1) Substitution führt immer zum Integral eines rationalen Bruchs. In einigen Fällen gibt es jedoch Ersetzungen (diese werden unten dargestellt), die zu kürzeren Berechnungen führen. Rationale Funktionen von.
2) Wenn R und alle Konstanten, die die Operationen Addition, Subtraktion, Multiplikation, Division und Potenzierung verwenden. Sie werden wie folgt bezeichnet: R cos x → - cos x 3) Wenn R beim Ersetzen mit -1 multipliziert Sünde x.
Sünde x → - Sünde x und alle Konstanten, die die Operationen Addition, Subtraktion, Multiplikation, Division und Potenzierung verwenden. Sie werden wie folgt bezeichnet: Rändert sich nicht wie beim gleichzeitigen Austausch 1) Substitution führt immer zum Integral eines rationalen Bruchs. In einigen Fällen gibt es jedoch Ersetzungen (diese werden unten dargestellt), die zu kürzeren Berechnungen führen., Und 3) Wenn R, dann ist die Substitution t = tg x oder t = ctg x.

Beispiele:
, , .

Produkt der Potenzfunktionen von cos x und sin x

Integrale der Form

sind Integrale rationaler trigonometrischer Funktionen. Daher können die im vorherigen Abschnitt beschriebenen Methoden auf sie angewendet werden. Nachfolgend werden Methoden besprochen, die auf den Besonderheiten solcher Integrale basieren.

Wenn m und n rationale Zahlen sind, dann ist eine der Substitutionen t = Rationale Funktionen von oder t = Sünde x das Integral wird auf das Integral des Differentialbinomials reduziert.

Wenn m und n ganze Zahlen sind, erfolgt die Integration mithilfe von Reduktionsformeln:

;
;
;
.

Beispiel:
.

Integrale des Produkts eines Polynoms und Sinus oder Cosinus

Integrale der Form:
, ,
wobei P(x) ein Polynom in x ist, werden in Teilen integriert. Dabei ergeben sich folgende Formeln:

;
.

Beispiele:
, .

Integrale des Produkts aus Polynom, Exponential und Sinus oder Cosinus

Integrale der Form:
, ,
wobei P(x) ein Polynom in x ist, das mithilfe der Euler-Formel integriert wurde
e iax = cos ax + isin ax(wobei i 2 = - 1 ).
Berechnen Sie dazu das Integral mit der im vorherigen Absatz beschriebenen Methode
.
Durch die Trennung von Real- und Imaginärteil aus dem Ergebnis erhält man die ursprünglichen Integrale.

Beispiel:
.

Nicht standardmäßige Methoden zur Integration trigonometrischer Funktionen

Im Folgenden finden Sie eine Reihe nicht standardmäßiger Methoden, mit denen Sie die Integration trigonometrischer Funktionen durchführen oder vereinfachen können.

Abhängigkeit von (a sin x + b cos x)

Wenn der Integrand nur von a abhängt sin x + b cos x, dann ist es sinnvoll, die Formel anzuwenden:
,
Wo .

Zum Beispiel

Brüche aus Sinus und Cosinus in einfachere Brüche auflösen

Betrachten Sie das Integral
.
Die einfachste Integrationsmethode besteht darin, den Bruch mithilfe der Transformation in einfachere zu zerlegen:
sin(a - b) = sin(x + a - (x + b)) = sin(x+a) cos(x+b) - cos(x+a) sin(x+b)

Integrieren von Brüchen ersten Grades

Bei der Berechnung des Integrals
,
Es ist zweckmäßig, den ganzzahligen Teil des Bruchs und die Ableitung des Nenners zu isolieren
A 1 sin x + b 1 cos x = A (a sin x + b cos x) + B (a sin x + b cos x)′ .
Die Konstanten A und B werden durch Vergleich der linken und rechten Seite ermittelt.

Verwendete Literatur:
N.M. Gunter, R.O. Kuzmin, Sammlung von Problemen Höhere Mathematik, „Lan“, 2003.

Siehe auch: