1. Improper integrals with infinite limits
Let us recall the definition of an integral as the limit of integral sums: 
The definition assumes that the integration interval is finite and the function f(x) is continuous within it. Violation of these assumptions leads to improper integrals.
Definition. If the integral tends to a finite limit as it increases indefinitely "b", then this limit is called an improper integral with an infinite upper bound of the function f (x) and is denoted by the symbol 
In this case, the improper integral is said to exist or converge.
If the specified limit does not exist or exists but is infinite, then the integral is said to not exist or to diverge.
An improper integral with an infinite lower bound is defined similarly:

An improper integral with two infinite boundaries is given by:

where c is any fixed point on the Ox axis.
So, improper integrals can have an infinite lower bound, an infinite upper bound, and also two infinite bounds.
Signs of convergence. Absolute and conditional convergence
An integral exists only if each of the integrals exists: and .
Example. Examine the convergence of the integral
Assuming c = 0, we get:

those. the integral converges.
Sometimes there is no need to calculate an improper integral, but it is enough to just know whether it converges or diverges by comparing it with another integral.
Comparison theorem for improper integrals.
Let the function f (x) in the interval have several (finite number) discontinuity points of the first kind, this “obstacle” can be easily eliminated by dividing the segment into several segments with discontinuity points, calculating definite integrals on each individual section and adding up the results.
Let us consider the definite integral of a function that is unlimited when approaching one of the ends of the segment, for example, ![]() .
.
(In such cases they usually say: ''The function has an infinite discontinuity at the right end of the interval of integration.''.)
It is clear that the usual definition of an integral loses its meaning here.
Definition. An improper integral of the function f(x), continuous for a £ x< b и неограниченной при x ® b - 0, называется предел:

The improper integral of a function that has an infinite discontinuity at the left end of the segment is defined similarly:

Consequently, in the section [-1, 0] the integral diverges.

This means that the integral also diverges in the section.
Thus, this integral diverges over the entire interval [-1, 1]. Note that if we began to calculate this integral without paying attention to the discontinuity of the integrand at the point x = 0, we would get an incorrect result. Really,
 , which is impossible.
, which is impossible.
So, to study the improper integral of a discontinuous function, it is necessary to “split” it into several integrals and study them.
As you know, finding the integral can be a rather difficult task. It would be a great disappointment to start calculating an improper integral and find at the end of the path that it diverges. Therefore, of interest are methods that allow, without serious calculations based on one type of function, to draw a conclusion about the convergence or divergence of an improper integral. The first and second comparison theorems, which will be discussed below, greatly help to study improper integrals for convergence.
Let f(x)?0. Then the functions
are monotonically increasing in the variables t or -g (since we take g>0, -g tends to zero from the left). If, as the arguments increase, the functions F 1 (t) and F 2 (-d) remain bounded from above, this means that the corresponding improper integrals converge. This is the basis of the first comparison theorem for integrals of non-negative functions.
Let the functions f(x) and g(x) at x?a satisfy the following conditions:
- 1) 0?f(x)?g(x);
- 2) The functions f(x) and g(x) are continuous.
Then from the convergence of the integral follows the convergence of the integral, and from the divergence of the integral follows the divergence
Since 0?f(x)?g(x) and the functions are continuous, then
By condition, the integral converges, i.e. has a finite value. Therefore, the integral also converges.
Now let the integral diverge. Let us assume that the integral converges, but then the integral must converge, which contradicts the condition. Our assumption is incorrect, the integral diverges.
Comparison theorem for improper integrals of the 2nd kind.
Let for the functions f(x) and g(x) on the interval , increase without limit for x>+0. For x>+0, the following inequality holds:<. Несобственный интеграл есть эталонный интеграл 2-го рода, который при p=<1 сходится; следовательно, по 1-й теореме сравнения для несобственных интегралов 2-го рода интеграл сходится также.
Comparison theorem for improper integrals of the 1st kind.
Let the function f(x) and g(x) be on the interval , and the integration segment is finite, that is, limited by numbers and not by infinity. Some tasks lead to the need to abandon these restrictions. This is how improper integrals appear.
Geometric meaning of the improper integral It turns out quite simply. In the case when the graph of a function y = f(x) is above the axis Ox, the definite integral expresses the area of a curvilinear trapezoid bounded by a curve y = f(x) , x-axis and ordinates x = a , x = b. In turn, the improper integral expresses the area of an unlimited (infinite) curvilinear trapezoid enclosed between the lines y = f(x) (in the picture below - red), x = a and the abscissa axis.

Improper integrals are defined similarly for other infinite intervals:
The area of an infinite curved trapezoid can be a finite number, in which case the improper integral is called convergent. The area can also be infinity, and in this case the improper integral is called divergent.
Using the limit of an integral instead of the improper integral itself. In order to evaluate the improper integral, you need to use the limit definite integral. If this limit exists and is finite (not equal to infinity), then the improper integral is called convergent, and otherwise - divergent. What a variable tends to under the limit sign depends on whether we are dealing with an improper integral of the first kind or of the second kind. Let's find out about this now.
Improper integrals of the first kind - with infinite limits and their convergence
Improper integrals with infinite upper limit
So, writing an improper integral differs from the usual definite integral in that the upper limit of integration is infinite.
Definition. An improper integral with an infinite upper limit of integration of a continuous function f(x) in the interval from a before ∞ the limit of the integral of this function with the upper limit of integration is called b and the lower limit of integration a provided that the upper limit of integration grows without limit, i.e.
![]() .
.
If this limit exists and is equal to some number rather than infinity, then an improper integral is called convergent, and the number to which the limit is equal is taken as its value. Otherwise an improper integral is called divergent and no meaning is attributed to it.
Example 1. Calculate improper integral(if it converges).
Solution. Based on the definition of the improper integral, we find

Since the limit exists and is equal to 1, then this improper integral converges and is equal to 1.
In the following example, the integrand is almost the same as in example 1, only the degree x is not two, but the letter alpha, and the task is to study the improper integral for convergence. That is, the question remains to be answered: at what values of alpha does this improper integral converge, and at what values does it diverge?
Example 2. Examine the improper integral for convergence(the lower limit of integration is greater than zero).
Solution. Let us first assume that , then

In the resulting expression, we move to the limit at:
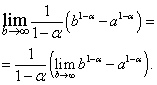
It is easy to see that the limit on the right side exists and is equal to zero when , that is , and does not exist when , that is .
In the first case, that is, when . If , then  and doesn't exist.
and doesn't exist.
The conclusion of our study is as follows: this improper integral converges at and diverges at .
Applying the Newton-Leibniz formula to the type of improper integral being studied ![]() , you can derive the following formula, which is very similar to it:
, you can derive the following formula, which is very similar to it:
 .
.
This is a generalized Newton-Leibniz formula.
Example 3. Calculate improper integral(if it converges).
The limit of this integral exists:
![]()
The second integral, making up the sum expressing the original integral:

The limit of this integral also exists:
![]() .
.
We find the sum of two integrals, which is also the value of the original improper integral with two infinite limits:
Improper integrals of the second kind - from unbounded functions and their convergence
Let the function f(x) given on the segment from a before b and is unlimited on it. Suppose that the function goes to infinity at the point b , while at all other points of the segment it is continuous.
Definition. An improper integral of a function f(x) on the segment from a before b the limit of the integral of this function with the upper limit of integration is called c , if when striving c To b the function increases without limit, and at the point x = b function not defined, i.e.
![]() .
.
If this limit exists, then the improper integral of the second kind is called convergent, otherwise it is called divergent.
Using the Newton-Leibniz formula, we derive.
If the integrand has a discontinuity of the second kind on the (finite) interval of integration, we speak of an improper integral of the second kind.
10.2.1 Definition and basic properties
Let us denote the integration interval by $\left[ a, \, b \right ]$; both of these numbers are assumed to be finite below. If there is only 1 discontinuity, it can be located either at point $a$, or at point $b$, or inside the interval $(a,\,b)$. Let us first consider the case when there is a discontinuity of the second kind at point $a$, and at other points the integrand function is continuous. So we are discussing the integral
\begin(equation) I=\int _a^b f(x)\,dx, (22) \label(intr2) \end(equation)
and $f(x) \rightarrow \infty $ when $x \rightarrow a+0$. As before, the first thing to do is to give meaning to this expression. To do this, consider the integral
\[ I(\epsilon)=\int _(a+\epsilon)^b f(x)\,dx. \]
Definition. Let there be a finite limit
\[ A=\lim _(\epsilon \rightarrow +0)I(\epsilon)=\lim _(\epsilon \rightarrow +0)\int _(a+\epsilon)^b f(x)\,dx. \]
Then the improper integral of the second kind (22) is said to converge and the value $A$ is assigned to it; the function $f(x)$ itself is said to be integrable on the interval $\left[ a, \, b\right]$.
Consider the integral
\[ I=\int ^1_0\frac(dx)(\sqrt(x)). \]
The integrand function $1/\sqrt(x)$ at $x \rightarrow +0$ has an infinite limit, so at the point $x=0$ it has a discontinuity of the second kind. Let's put
\[ I(\epsilon)=\int ^1_(\epsilon )\frac(dx)(\sqrt(x))\,. \]
In this case, the antiderivative is known,
\[ I(\epsilon)=\int ^1_(\epsilon )\frac(dx)(\sqrt(x))=2\sqrt(x)|^1_(\epsilon )=2(1-\sqrt( \epsilon ))\rightarrow 2\]
at $\epsilon \rightarrow +0$. Thus, the original integral is a convergent improper integral of the second kind, and it is equal to 2.
Let us consider the option when there is a discontinuity of the second kind in the integrand function at the upper limit of the integration interval. This case can be reduced to the previous one by making the change of variable $x=-t$ and then rearranging the limits of integration.
Let us consider the option when the integrand function has a discontinuity of the second kind inside the integration interval, at point $c \in (a,\,b)$. In this case, the original integral
\begin(equation) I=\int _a^bf(x)\,dx (23) \label(intr3) \end(equation)
presented as a sum
\[ I=I_1+I_2, \quad I_1=\int _a^cf(x)\,dx +\int _c^df(x)\,dx. \]
Definition. If both integrals $I_1, \, I_2$ converge, then the improper integral (23) is called convergent and is assigned a value equal to the sum of the integrals $I_1, \, I_2$, the function $f(x)$ is called integrable on the interval $\left [a, \, b\right]$. If at least one of the integrals $I_1,\, I_2$ is divergent, the improper integral (23) is called divergent.
Convergent improper integrals of the 2nd kind have all the standard properties of ordinary definite integrals.
1. If $f(x)$, $g(x)$ are integrable on the interval $\left[ a, \,b \right ]$, then their sum $f(x)+g(x)$ is also integrable on this interval, and \[ \int _a^(b)\left(f(x)+g(x)\right)dx=\int _a^(b)f(x)dx+\int _a^(b)g (x)dx. \] 2. If $f(x)$ is integrable on the interval $\left[ a, \, b \right ]$, then for any constant $C$ the function $C\cdot f(x)$ is also integrable on this interval , and \[ \int _a^(b)C\cdot f(x)dx=C \cdot \int _a^(b)f(x)dx. \] 3. If $f(x)$ is integrable on the interval $\left[ a, \, b \right ]$, and on this interval $f(x)>0$, then \[ \int _a^(b ) f(x)dx\,>\,0. \] 4. If $f(x)$ is integrable on the interval $\left[ a, \, b \right ]$, then for any $c\in (a, \,b)$ the integrals \[ \int _a^ (c) f(x)dx, \quad \int _c^(b) f(x)dx \] also converge, and \[ \int _a^(b)f(x)dx=\int _a^(c ) f(x)dx+\int _c^(b) f(x)dx \] (additivity of the integral over the interval).
Consider the integral \begin(equation) I=\int _0^(1)\frac(1)(x^k)\,dx. (24) \label(mod2) \end(equation) If $k>0$, the integrand tends to $\infty$ as $x \rightarrow +0$, so the integral is improper of the second kind. Let's introduce the function \[ I(\epsilon)=\int _(\epsilon)^(1)\frac(1)(x^k)\,dx. \] In this case the antiderivative is known, so \[ I(\epsilon)=\int _(\epsilon)^(1)\frac(1)(x^k)\,dx\,=\frac(x^(1-k))(1-k )|_(\epsilon)^1= \frac(1)(1-k)-\frac(\epsilon ^(1-k))(1-k). \] for $k \neq 1$, \[ I(\epsilon)=\int _(\epsilon)^(1)\frac(1)(x)\,dx\,=lnx|_(\epsilon)^1= -ln \epsilon. \] for $k = 1$. Considering the behavior at $\epsilon \rightarrow +0$, we come to the conclusion that integral (20) converges at $k
10.2.2 Tests for the convergence of improper integrals of the 2nd kind
Theorem (the first sign of comparison). Let $f(x)$, $g(x)$ be continuous for $x\in (a,\,b)$, and $0 1. If the integral \[ \int _a^(b)g(x)dx \] converges, then the integral \[ \int _a^(b)f(x)dx converges. \] 2. If the integral \[ \int _a^(b)f(x)dx \] diverges, then the integral \[ \int _a^(b)g(x)dx diverges. \]
Theorem (second comparison criterion). Let $f(x)$, $g(x)$ be continuous and positive for $x\in (a,\,b)$, and let there be a finite limit
\[ \theta = \lim_(x \rightarrow a+0) \frac(f(x))(g(x)), \quad \theta \neq 0, \, +\infty. \]
Then the integrals
\[ \int _a^(b)f(x)dx, \quad \int _a^(b)g(x)dx \]
converge or diverge simultaneously.
Consider the integral
\[ I=\int _0^(1)\frac(1)(x+\sin x)\,dx. \]
The integrand is a positive function on the integration interval, the integrand tends to $\infty$ as $x \rightarrow +0$, so our integral is an improper integral of the second kind. Further, for $x \rightarrow +0$ we have: if $g(x)=1/x$, then
\[ \lim _(x \rightarrow +0)\frac(f(x))(g(x))=\lim _(x \rightarrow +0)\frac(x)(x+\sin x)=\ frac(1)(2) \neq 0,\, \infty \, . \]
Applying the second comparison criterion, we come to the conclusion that our integral converges or diverges simultaneously with the integral
\[ \int _0^(+1)\frac(1)(x)\,dx . \]
As was shown in the previous example, this integral diverges ($k=1$). Consequently, the original integral also diverges.
Calculate the improper integral or establish its convergence (divergence).
1. \[ \int _(0)^(1)\frac(dx)(x^3-5x^2)\,. \] 2. \[ \int _(3)^(7)\frac(x\,dx)((x-5)^2)\,. \] 3. \[ \int _(0)^(1)\frac(x\,dx)(\sqrt(1-x^2))\,. \] 4. \[ \int _(0)^(1)\frac(x^3\,dx)(1-x^5)\,. \] 5. \[ \int _(-3)^(2)\frac(dx)((x+3)^2)\,. \] 6. \[ \int _(1)^(2)\frac(x^2\,dx)((x-1)\sqrt(x-1))\,. \] 7. \[ \int _(0)^(1)\frac(dx)(\sqrt(x+x^2))\,. \] 8. \[ \int _(0)^(1/4)\frac(dx)(\sqrt(x-x^2))\,. \] 9. \[ \int _(1)^(2)\frac(dx)(xlnx)\,. \] 10. \[ \int _(1)^(2)\frac(x^3\,dx)(\sqrt(4-x^2))\,. \] 11. \[ \int _(0)^(\pi /4)\frac(dx)(\sin ^4x)\,. \]