ტრიგონომეტრიული ფუნქციების ინტეგრალები.
გადაწყვეტილებების მაგალითები

ამ გაკვეთილზე განვიხილავთ ტრიგონომეტრიული ფუნქციების ინტეგრალებს, ანუ ინტეგრალების შევსება იქნება სინუსები, კოსინუსები, ტანგენტები და კოტანგენტები სხვადასხვა კომბინაციებში. ყველა მაგალითი დეტალურად იქნება გაანალიზებული, ჩაიდანისთვისაც კი ხელმისაწვდომი და გასაგები.

ტრიგონომეტრიული ფუნქციების ინტეგრალების წარმატებით შესასწავლად, თქვენ კარგად უნდა გესმოდეთ უმარტივესი ინტეგრალები, ასევე დაეუფლოთ ინტეგრაციის ზოგიერთ ტექნიკას. თქვენ შეგიძლიათ გაეცნოთ ამ მასალებს ლექციებზე განუსაზღვრელი ინტეგრალი. გადაწყვეტილებების მაგალითებიდა .

და ახლა ჩვენ გვჭირდება: ინტეგრალების ცხრილი, წარმოებულების ცხრილიდა ტრიგონომეტრიული ფორმულების დირექტორია. ყველა მეთოდოლოგიური სახელმძღვანელოებიშეგიძლიათ იხილოთ გვერდზე მათემატიკური ფორმულები და ცხრილები. გირჩევ ყველაფრის დაბეჭდვას. მე განსაკუთრებით ვამახვილებ ყურადღებას ტრიგონომეტრიულ ფორმულებზე, ისინი თქვენს თვალწინ უნდა იყოს– ამის გარეშე მუშაობის ეფექტურობა შესამჩნევად შემცირდება.

მაგრამ ჯერ იმაზე, თუ რა ინტეგრალებია ამ სტატიაში არა. ფორმის ინტეგრალები არ არსებობს, - კოსინუსი, სინუსი, გამრავლებული რამდენიმე მრავალწევრზე (ნაკლებად ხშირად რაღაც ტანგენსი ან კოტანგენსი). ასეთი ინტეგრალები ინტეგრირებულია ნაწილების მიხედვით და მეთოდის შესასწავლად ეწვიეთ გაკვეთილს ინტეგრაცია ნაწილებით. გადაწყვეტილებების მაგალითები ასევე აქ არ არის ინტეგრალები "თაღებით" - არქტანგენტი, რკალი და ა.შ., ისინი ასევე ყველაზე ხშირად ინტეგრირებულია ნაწილებით.

ტრიგონომეტრიული ფუნქციების ინტეგრალების პოვნისას გამოიყენება რამდენიმე მეთოდი:

(4) ჩვენ ვიყენებთ ცხრილის ფორმულას , განსხვავება მხოლოდ ისაა, რომ "X"-ის ნაცვლად გვაქვს რთული გამოხატულება.

მაგალითი 2

მაგალითი 3

იპოვნეთ განუსაზღვრელი ინტეგრალი.

ჟანრის კლასიკა მათთვის, ვინც იხრჩობა კონკურსში. როგორც ალბათ შენიშნეთ, ინტეგრალების ცხრილში არ არის ტანგენსის და კოტანგენტის ინტეგრალი, მაგრამ, მიუხედავად ამისა, ასეთი ინტეგრალები შეიძლება მოიძებნოს.

(1) ჩვენ ვიყენებთ ტრიგონომეტრიულ ფორმულას

(2) ფუნქციას მივყავართ დიფერენციალური ნიშნის ქვეშ.

(3) ვიყენებთ ცხრილის ინტეგრალს .

მაგალითი 4

იპოვნეთ განუსაზღვრელი ინტეგრალი.

ეს არის მაგალითი დამოუკიდებელი ამოხსნისთვის, სრული ამოხსნა და პასუხი მოცემულია გაკვეთილის ბოლოს.

მაგალითი 5

იპოვნეთ განუსაზღვრელი ინტეგრალი.

ჩვენი ხარისხები თანდათან გაიზრდება =).
პირველი გამოსავალი:

(1) ჩვენ ვიყენებთ ფორმულას

(2) ჩვენ ვიყენებთ მთავარ ტრიგონომეტრიულ იდენტობას , საიდანაც გამომდინარეობს, რომ .

(3) გაყავით მრიცხველი მნიშვნელობით ტერმინით.

(4) ვიყენებთ განუსაზღვრელი ინტეგრალის წრფივობის თვისებას.

(5) ჩვენ ვაერთიანებთ ცხრილის გამოყენებით.

მაგალითი 6

იპოვნეთ განუსაზღვრელი ინტეგრალი.

ეს არის მაგალითი დამოუკიდებელი ამოხსნისთვის, სრული ამოხსნა და პასუხი მოცემულია გაკვეთილის ბოლოს.

ასევე არის ტანგენტების და კოტანგენტების ინტეგრალები, რომლებიც უფრო მეტშია მაღალი გრადუსი. გაკვეთილზე განიხილება ტანგენტის კუბის ინტეგრალი როგორ გამოვთვალოთ ბრტყელი ფიგურის ფართობი?მეოთხე და მეხუთე ხარისხების ტანგენტის (კოტანგენტის) ინტეგრალების მიღება შეგიძლიათ გვერდზე რთული ინტეგრალები.

ინტეგრანდის ხარისხის შემცირება

ეს ტექნიკა მუშაობს მაშინ, როდესაც ინტეგრანდული ფუნქციები ივსება სინუსებით და კოსინუსებით თუნდაცგრადუსი. ხარისხის გამოყენების შესამცირებლად ტრიგონომეტრიული ფორმულები , და, და ბოლო ფორმულა ხშირად გამოიყენება საპირისპირო მიმართულებით: .

მაგალითი 7

იპოვნეთ განუსაზღვრელი ინტეგრალი.

გამოსავალი:

პრინციპში, აქ ახალი არაფერია, გარდა იმისა, რომ ფორმულა გამოვიყენეთ (ინტეგრანდის ხარისხის დაქვეითება). გთხოვთ გაითვალისწინოთ, რომ მე შევამოკლე გამოსავალი. როგორც თქვენ მიიღებთ გამოცდილებას, ინტეგრალი შეგიძლიათ ნახოთ ზეპირად, ეს დაზოგავს დროს და საკმაოდ მისაღებია დავალების დასრულებისას. ამ შემთხვევაში, მიზანშეწონილია არ აღწეროთ წესი , ჯერ სიტყვიერად ვიღებთ 1-ის ინტეგრალს, შემდეგ --ს.

მაგალითი 8

იპოვნეთ განუსაზღვრელი ინტეგრალი.

ეს არის მაგალითი დამოუკიდებელი ამოხსნისთვის, სრული ამოხსნა და პასუხი მოცემულია გაკვეთილის ბოლოს.

ეს არის დაპირებული ხარისხის ზრდა:

მაგალითი 9

იპოვნეთ განუსაზღვრელი ინტეგრალი.

ჯერ გამოსავალი, მერე კომენტარები:

(1) მოამზადეთ ინტეგრანტი ფორმულის გამოსაყენებლად .

(2) ჩვენ რეალურად ვიყენებთ ფორმულას.

(3) მნიშვნელს კვადრატში ვაკეთებთ და ინტეგრალური ნიშნიდან ვიღებთ მუდმივას. შეიძლებოდა ცოტა სხვანაირად გაკეთებულიყო, მაგრამ, ჩემი აზრით, უფრო მოსახერხებელი იყო.

(4) ჩვენ ვიყენებთ ფორმულას

(5) მესამე ტერმინში ჩვენ კვლავ ვამცირებთ ხარისხს, მაგრამ ფორმულის გამოყენებით .

(6) წარმოგიდგენთ მსგავსი ტერმინები(აქ მე დავყავი და გააკეთა დამატება).

(7) რეალურად, ჩვენ ვიღებთ ინტეგრალს, წრფივობის წესს ხოლო დიფერენციალური ნიშნით ფუნქციის შეყვანის მეთოდი ზეპირად სრულდება.

(8) პასუხის კომბინირება.

! განუსაზღვრელი ინტეგრალში პასუხი ხშირად შეიძლება რამდენიმე გზით დაიწეროს

ახლახან განხილულ მაგალითში საბოლოო პასუხი შეიძლებოდა სხვაგვარად დაეწერა - ფრჩხილების გახსნა და ამის გაკეთებაც კი გამოხატვის ინტეგრირებამდე, ანუ მაგალითის შემდეგი დასასრული სავსებით მისაღებია:

სავსებით შესაძლებელია, რომ ეს ვარიანტი კიდევ უფრო მოსახერხებელი იყოს, მე უბრალოდ ავუხსენი ისე, როგორც მე მიჩვეული ვიყავი მის გადაჭრას). აქ არის კიდევ ერთი ტიპიური მაგალითი დამოუკიდებელი გადაწყვეტისთვის:

მაგალითი 10

იპოვნეთ განუსაზღვრელი ინტეგრალი.

ეს მაგალითი შეიძლება გადაწყდეს ორი გზით და შეიძლება წარმატებას მიაღწიოთ ორი სრულიად განსხვავებული პასუხი(უფრო ზუსტად, ისინი სრულიად განსხვავებულად გამოიყურებიან, მაგრამ მათემატიკური თვალსაზრისით ისინი ექვივალენტური იქნებიან). სავარაუდოდ, თქვენ ვერ ნახავთ ყველაზე რაციონალურ მეთოდს და დაზარალდებით ფრჩხილების გახსნით და სხვა ტრიგონომეტრიული ფორმულებით. ყველაზე ეფექტური გამოსავალი მოცემულია გაკვეთილის ბოლოს.

აბზაცის შესაჯამებლად დავასკვნით: ფორმის ნებისმიერი ინტეგრალი , სად და - თუნდაცრიცხვები, იხსნება ინტეგრადის ხარისხის შემცირების მეთოდით.
პრაქტიკაში შემხვდა 8 და 10 გრადუსიანი ინტეგრალები და მათი საშინელი არეულობის მოგვარება მომიწია ხარისხის რამდენჯერმე დაწევით, რასაც მოჰყვა გრძელი, გრძელი პასუხები.

ცვლადის ჩანაცვლების მეთოდი

როგორც სტატიაშია აღნიშნული ცვლადის ცვლილების მეთოდი განუსაზღვრელი ინტეგრალშიჩანაცვლების მეთოდის გამოყენების მთავარი წინაპირობაა ის ფაქტი, რომ ინტეგრანდში არის გარკვეული ფუნქცია და მისი წარმოებული:
(ფუნქციები სულაც არ არის პროდუქტში)

მაგალითი 11

იპოვნეთ განუსაზღვრელი ინტეგრალი.

ჩვენ ვუყურებთ წარმოებულების ცხრილს და ვამჩნევთ ფორმულებს, , ანუ ჩვენს ინტეგრანდში არის ფუნქცია და მისი წარმოებული. თუმცა ვხედავთ, რომ დიფერენციაციის დროს კოსინუსი და სინუსი ურთიერთგადაიქცევა ერთმანეთში და ჩნდება კითხვა: როგორ უნდა შესრულდეს ცვლადის ცვლილება და რას ვგულისხმობთ სინუსში ან კოსინუსში?! კითხვა შეიძლება გადაწყდეს მეცნიერული ჩხუბით: თუ ჩანაცვლებას არასწორად შევასრულებთ, კარგი არაფერი გამოვა.

ზოგადი სახელმძღვანელო: მსგავს შემთხვევებში, თქვენ უნდა მიუთითოთ ფუნქცია, რომელიც არის მნიშვნელში.

ჩვენ ვწყვეტთ ხსნარს და ვაკეთებთ ჩანაცვლებას

მნიშვნელში ყველაფერი კარგადაა, ყველაფერი მხოლოდ ზეა დამოკიდებული, ახლა რჩება იმის გარკვევა, თუ რაში გადაიქცევა.
ამისათვის ჩვენ ვპოულობთ დიფერენციალს:

ან მოკლედ:
შედეგად მიღებული თანასწორობიდან, პროპორციის წესის გამოყენებით, ჩვენ გამოვხატავთ გამოთქმას, რომელიც გვჭირდება:

ასე რომ:

ახლა მთელი ჩვენი ინტეგრაცია დამოკიდებულია მხოლოდ და ჩვენ შეგვიძლია გავაგრძელოთ გადაჭრა

მზადაა. შეგახსენებთ, რომ ჩანაცვლების მიზანია ინტეგრანტის გამარტივება, ამ შემთხვევაში ყველაფერი გადავიდა დენის ფუნქციის ინტეგრირებაზე ცხრილის მიხედვით.

შემთხვევითი არ არის, რომ ეს მაგალითი ასე დეტალურად გაკეთდა გაკვეთილის მასალის განმეორებისა და განმტკიცების მიზნით ცვლადის ცვლილების მეთოდი განუსაზღვრელი ინტეგრალში.

ახლა კი ორი მაგალითი საკუთარი გადაწყვეტისთვის:

მაგალითი 12

იპოვნეთ განუსაზღვრელი ინტეგრალი.

მაგალითი 13

იპოვნეთ განუსაზღვრელი ინტეგრალი.

შეავსეთ გადაწყვეტილებები და პასუხები გაკვეთილის ბოლოს.

მაგალითი 14

იპოვნეთ განუსაზღვრელი ინტეგრალი.

აქ ისევ ინტეგრანდში არის სინუსი და კოსინუსი (ფუნქცია წარმოებულთან), მაგრამ ნამრავლში და ჩნდება დილემა - რას ვგულისხმობთ სინუსში თუ კოსინუსში?

თქვენ შეგიძლიათ სცადოთ ჩანაცვლების განხორციელება სამეცნიერო პოკინგის გამოყენებით, და თუ არაფერი არ მუშაობს, მაშინ მიუთითეთ იგი სხვა ფუნქციად, მაგრამ არის:

ზოგადი მითითება: თქვენ უნდა მიუთითოთ ფუნქცია, რომელიც, ფიგურალურად რომ ვთქვათ, არის „არასასიამოვნო მდგომარეობაში“.

ჩვენ ვხედავთ, რომ ამ მაგალითში სტუდენტის კოსინუსი "იტანჯება" ხარისხით და სინუსი თავისუფლად ზის, თავისთავად.

ამიტომ, მოდით გავაკეთოთ ჩანაცვლება:

თუ ვინმეს მაინც უჭირს ცვლადის ჩანაცვლებისა და დიფერენციალის პოვნის ალგორითმი, მაშინ უნდა დაუბრუნდეთ გაკვეთილს ცვლადის ცვლილების მეთოდი განუსაზღვრელი ინტეგრალში.

მაგალითი 15

იპოვნეთ განუსაზღვრელი ინტეგრალი.

გავაანალიზოთ ინტეგრანტი, რითი უნდა აღინიშნოს?
გავიხსენოთ ჩვენი მითითებები:
1) ფუნქცია დიდი ალბათობით არის მნიშვნელში;
2) ფუნქცია არის „უხერხულ მდგომარეობაში“.

სხვათა შორის, ეს მითითებები მოქმედებს არა მხოლოდ ტრიგონომეტრიული ფუნქციებისთვის.

სინუსი შეესაბამება ორივე კრიტერიუმს (განსაკუთრებით მეორეს), ამიტომ ჩანაცვლება თავს გვთავაზობს. პრინციპში, ჩანაცვლება უკვე შეიძლება განხორციელდეს, მაგრამ ჯერ კარგი იქნებოდა გაერკვია რა უნდა გააკეთოს? ჯერ ერთ კოსინუსს „ვაჭერთ“:

ჩვენ ვიტოვებთ ჩვენს "მომავალ" დიფერენციალს

და ჩვენ გამოვხატავთ მას სინუსების მეშვეობით მთავარის გამოყენებით ტრიგონომეტრიული იდენტურობა:

ახლა აქ არის ჩანაცვლება:

ზოგადი წესი: თუ ინტეგრანდში ერთ-ერთი ტრიგონომეტრიული ფუნქცია (სინუსი ან კოსინუსი) არის უცნაურიხარისხით, მაშინ თქვენ უნდა „ამოიღოთ“ ერთი ფუნქცია კენტი ხარისხისგან და დანიშნოთ სხვა ფუნქცია მის უკან.ჩვენ ვსაუბრობთ მხოლოდ ინტეგრალებზე, სადაც არის კოსინუსები და სინუსები.

განხილულ მაგალითში ჩვენ გვქონდა კოსინუსი კენტი სიმძლავრის მქონე, ასე რომ, ჩვენ ამოვიღეთ ერთი კოსინუსი სიმძლავრისგან და აღვნიშნეთ ის, როგორც სინუსი.

მაგალითი 16

იპოვნეთ განუსაზღვრელი ინტეგრალი.

გრადუსი აფრენა =).
ეს არის მაგალითი თქვენთვის, რომ გადაჭრათ საკუთარი. სრული ამოხსნა და პასუხი გაკვეთილის ბოლოს.

უნივერსალური ტრიგონომეტრიული ჩანაცვლება

უნივერსალური ტრიგონომეტრიული ჩანაცვლება ცვლადის ჩანაცვლების მეთოდის ჩვეულებრივი შემთხვევაა. შეგიძლიათ სცადოთ მისი გამოყენება, როდესაც „არ იცით რა გააკეთოთ“. მაგრამ სინამდვილეში არსებობს გარკვეული მითითებები მისი გამოყენებისთვის. ტიპიური ინტეგრალები, სადაც საჭიროა უნივერსალური ტრიგონომეტრიული ჩანაცვლება, არის შემდეგი ინტეგრალები: , , , და ა.შ.

მაგალითი 17

იპოვნეთ განუსაზღვრელი ინტეგრალი.

უნივერსალური ტრიგონომეტრიული ჩანაცვლება ამ შემთხვევაში ხორციელდება შემდეგნაირად. მოდით შევცვალოთ: . ასოს არ ვიყენებ, მაგრამ ასოს, ეს არ არის ერთგვარი წესი, უბრალოდ, ისევ მიჩვეული ვარ საკითხების ასე გადაჭრას.

აქ უფრო მოსახერხებელია ამისთვის დიფერენციალის პოვნა, თანასწორობიდან გამოვხატავ:
ორივე ნაწილს ვამაგრებ არქტანგენტს:

არქტანგენსი და ტანგენსი ანადგურებენ ერთმანეთს:

ამრიგად:

პრაქტიკაში, თქვენ არ გჭირდებათ ამის აღწერა ასეთი დეტალურად, მაგრამ უბრალოდ გამოიყენეთ დასრულებული შედეგი:

! გამოთქმა მოქმედებს მხოლოდ იმ შემთხვევაში, თუ სინუსებისა და კოსინუსების ქვეშ გვაქვს უბრალოდ "X", ინტეგრალისთვის (რაზეც მოგვიანებით ვისაუბრებთ) ყველაფერი ცოტა სხვანაირად იქნება!

ჩანაცვლებისას სინუსები და კოსინუსები გადაიქცევა შემდეგ წილადებად:
, , ეს ტოლობები დაფუძნებულია ცნობილ ტრიგონომეტრიულ ფორმულებზე: ,

ასე რომ, საბოლოო დიზაინი შეიძლება ასე გამოიყურებოდეს:

მოდით განვახორციელოთ უნივერსალური ტრიგონომეტრიული ჩანაცვლება:

ასევე იქნება თქვენთვის გადასაჭრელი ამოცანები, რომლებზეც შეგიძლიათ ნახოთ პასუხები.

ინტეგრადი შეიძლება გარდაიქმნას ტრიგონომეტრიული ფუნქციების ნამრავლიდან ჯამზე

განვიხილოთ ინტეგრალები, რომლებშიც ინტეგრადი არის x-ის პირველი ხარისხის სინუსებისა და კოსინუსების ნამრავლი, გამრავლებული სხვადასხვა ფაქტორზე, ანუ ფორმის ინტეგრალებზე.

ცნობილი ტრიგონომეტრიული ფორმულების გამოყენება

(2)
(3)
(4)
შეიძლება თითოეული პროდუქტი (31) ფორმის ინტეგრალებში გარდაქმნას ალგებრულ ჯამად და ინტეგრირება ფორმულების მიხედვით

(5)

(6)

მაგალითი 1.იპოვე

გამოსავალი. ფორმულის მიხედვით (2) at

მაგალითი 2.იპოვე ტრიგონომეტრიული ფუნქციის ინტეგრალი

გამოსავალი. ფორმულის მიხედვით (3) at

მაგალითი 3.იპოვე ტრიგონომეტრიული ფუნქციის ინტეგრალი

გამოსავალი. ფორმულის მიხედვით (4) at ჩვენ ვიღებთ ინტეგრანტის შემდეგ ტრანსფორმაციას:

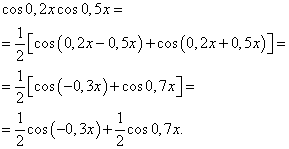
ფორმულის (6) გამოყენებით ვიღებთ

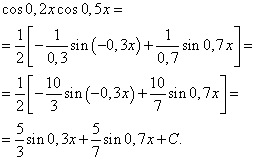
ერთი და იგივე არგუმენტის სინუსის და კოსინუსის ხარისხების ნამრავლის ინტეგრალი

ახლა განვიხილოთ ფუნქციების ინტეგრალები, რომლებიც წარმოადგენენ იმავე არგუმენტის სინუსებისა და კოსინუსების სიძლიერეებს, ე.ი.

(7)

განსაკუთრებულ შემთხვევებში, ერთ-ერთი მაჩვენებელი ( მან ნ) შეიძლება იყოს ნული.

ასეთი ფუნქციების ინტეგრირებისას გამოიყენება, რომ კოსინუსის ლუწი ხარისხი შეიძლება გამოიხატოს სინუსის მეშვეობით, ხოლო სინუსის დიფერენციალი უდრის cos x dx(ან თუნდაც სინუსის სიმძლავრე შეიძლება გამოიხატოს კოსინუსის სახით, ხოლო კოსინუსის დიფერენციალი უდრის - ცოდვას x dx ) .

უნდა განვასხვავოთ ორი შემთხვევა: 1) მინიმუმ ერთი ინდიკატორი მდა ნკენტი; 2) ორივე მაჩვენებელი თანაბარია.

დაე, მოხდეს პირველი შემთხვევა, კერძოდ ინდიკატორი ნ = 2კ+ 1 - კენტი. შემდეგ, იმის გათვალისწინებით, რომ

ინტეგრანტი წარმოდგენილია ისე, რომ მისი ერთი ნაწილი არის მხოლოდ სინუსის ფუნქცია, ხოლო მეორე არის სინუსის დიფერენციალი. ახლა იყენებთ ცვლადის ჩანაცვლებას ტ= ცოდვა xამოხსნა მცირდება პოლინომის ინტეგრირებამდე ტ. თუ მხოლოდ ხარისხი მუცნაურია, შემდეგ ისინი აკეთებენ იგივეს, იზოლირებენ ცოდვის ფაქტორს x, დანარჩენი ინტეგრადის გამოხატვა cos-ით xდა სჯერა ტ= cos x. ეს ტექნიკა ასევე შეიძლება გამოყენებულ იქნას, როდესაც სინუსის და კოსინუსის კოეფიციენტური ძალების ინტეგრირება , როდის ერთი ინდიკატორი მაინც უცნაურია . მთელი საქმე იმაშია სინუსის და კოსინუსის ხარისხების კოეფიციენტი მათი ნაწარმოების განსაკუთრებული შემთხვევაა : როდესაც ტრიგონომეტრიული ფუნქცია ინტეგრანის მნიშვნელშია, მისი ხარისხი უარყოფითია. მაგრამ ასევე არის ნაწილობრივი ტრიგონომეტრიული ფუნქციების შემთხვევები, როდესაც მათი ძალა მხოლოდ ლუწია. მათ შესახებ - მომდევნო აბზაცში.

თუ ორივე ინდიკატორი მდა ნ- მაშინაც კი, ტრიგონომეტრიული ფორმულების გამოყენებით

შეამცირეთ სინუსის და კოსინუსის მაჩვენებლები, რის შემდეგაც მიიღება იგივე ტიპის ინტეგრალი, როგორც ზემოთ. შესაბამისად, ინტეგრაცია უნდა გაგრძელდეს იმავე სქემის მიხედვით. თუ ლუწი მაჩვენებლებიდან ერთ-ერთი უარყოფითია, ანუ განიხილება სინუსისა და კოსინუსის ლუწი სიძლიერის კოეფიციენტი, მაშინ ეს სქემა არ არის შესაფერისი. . შემდეგ გამოიყენება ცვლადის ცვლილება იმისდა მიხედვით, თუ როგორ შეიძლება მოხდეს ინტეგრანტის გარდაქმნა. ასეთი შემთხვევა განიხილება შემდეგ პუნქტში.

მაგალითი 4.იპოვე ტრიგონომეტრიული ფუნქციის ინტეგრალი

გამოსავალი. კოსინუსის მაჩვენებელი უცნაურია. ამიტომ, წარმოვიდგინოთ

ტ= ცოდვა x(მაშინ dt= cos x dx ). შემდეგ მივიღებთ

ძველ ცვლადს რომ დავუბრუნდეთ, საბოლოოდ ვპოულობთ

მაგალითი 5.იპოვე ტრიგონომეტრიული ფუნქციის ინტეგრალი

.

გამოსავალი. კოსინუსის მაჩვენებელი, როგორც წინა მაგალითში, არის უცნაური, მაგრამ უფრო დიდი. წარმოვიდგინოთ

და გააკეთეთ ცვლადის ცვლილება ტ= ცოდვა x(მაშინ dt= cos x dx ). შემდეგ მივიღებთ

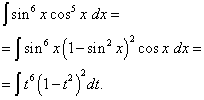
გავხსნათ ფრჩხილები

და ვიღებთ

ძველ ცვლადს რომ დავუბრუნდეთ, მივიღებთ გამოსავალს

მაგალითი 6.იპოვე ტრიგონომეტრიული ფუნქციის ინტეგრალი

გამოსავალი. სინუსის და კოსინუსის მაჩვენებლები ლუწია. ამრიგად, ჩვენ ვცვლით ინტეგრანდულ ფუნქციას შემდეგნაირად:

შემდეგ მივიღებთ

მეორე ინტეგრალში ვაკეთებთ ცვლადის, პარამეტრის შეცვლას ტ= ცოდვა2 x. მერე (1/2)dt= cos2 x dx . აქედან გამომდინარე,

ბოლოს მივიღებთ

ცვლადის ჩანაცვლების მეთოდის გამოყენება

ცვლადის ჩანაცვლების მეთოდიტრიგონომეტრიული ფუნქციების ინტეგრირებისას, ის შეიძლება გამოყენებულ იქნას იმ შემთხვევებში, როდესაც ინტეგრადი შეიცავს მხოლოდ სინუსს ან მხოლოდ კოსინუსს, სინუსის და კოსინუსის ნამრავლს, რომელშიც სინუსი ან კოსინუსი არის პირველ ხარისხში, ტანგენტი ან კოტანგენსი, ისევე როგორც კოეფიციენტი. ერთი და იგივე არგუმენტის სინუსის და კოსინუსის სიძლიერეც კი. ამ შემთხვევაში შესაძლებელია პერმუტაციების შესრულება არა მხოლოდ ცოდვაში x = ტდა ცოდვა x = ტ, არამედ ტგ x = ტდა ctg x = ტ .

მაგალითი 8.იპოვე ტრიგონომეტრიული ფუნქციის ინტეგრალი

.

გამოსავალი. შევცვალოთ ცვლადი: , შემდეგ . შედეგად მიღებული ინტეგრანტი შეიძლება ადვილად იყოს ინტეგრირებული ინტეგრალების ცხრილის გამოყენებით:

.

მაგალითი 9.იპოვე ტრიგონომეტრიული ფუნქციის ინტეგრალი

გამოსავალი. გადავიყვანოთ ტანგენსი სინუსისა და კოსინუსის თანაფარდობაში:

შევცვალოთ ცვლადი: , შემდეგ . შედეგად მიღებული ინტეგრანტი არის მაგიდის ინტეგრალიმინუს ნიშნით:

.

თავდაპირველ ცვლადს რომ დავუბრუნდეთ, საბოლოოდ მივიღებთ:

.

მაგალითი 10.იპოვე ტრიგონომეტრიული ფუნქციის ინტეგრალი

გამოსავალი. შევცვალოთ ცვლადი: , მაშინ .

მოდით გარდავქმნათ ინტეგრანტი ტრიგონომეტრიული იდენტობის გამოსაყენებლად :

ჩვენ ვცვლით ცვლადს, არ გვავიწყდება ინტეგრალის წინ მინუს ნიშნის დადება (იხ. ზემოთ, რა უდრის dt). შემდეგი, ჩვენ ვაფასებთ ინტეგრანდს და ვაერთიანებთ ცხრილის გამოყენებით:

თავდაპირველ ცვლადს რომ დავუბრუნდეთ, საბოლოოდ მივიღებთ:

.

თავად იპოვეთ ტრიგონომეტრიული ფუნქციის ინტეგრალი და შემდეგ გადახედეთ ამოხსნას

უნივერსალური ტრიგონომეტრიული ჩანაცვლება

უნივერსალური ტრიგონომეტრიული ჩანაცვლება შეიძლება გამოყენებულ იქნას იმ შემთხვევებში, როდესაც ინტეგრანი არ მიეკუთვნება წინა აბზაცებში განხილულ შემთხვევებს. ძირითადად, როდესაც სინუსი ან კოსინუსი (ან ორივე) არის წილადის მნიშვნელში. დადასტურებულია, რომ სინუსი და კოსინუსი შეიძლება შეიცვალოს სხვა გამოსახულებით, რომელიც შეიცავს თავდაპირველი კუთხის ნახევარის ტანგენტს შემდეგნაირად:

მაგრამ გაითვალისწინეთ, რომ უნივერსალური ტრიგონომეტრიული ჩანაცვლება ხშირად იწვევს საკმაოდ რთულ ალგებრულ გარდაქმნებს, ამიტომ ის საუკეთესოდ გამოიყენება, როდესაც სხვა მეთოდი არ იმუშავებს. მოდით შევხედოთ მაგალითებს, სადაც უნივერსალურ ტრიგონომეტრიულ ჩანაცვლებასთან ერთად გამოიყენება დიფერენციალური ნიშნით ჩანაცვლება და განუსაზღვრელი კოეფიციენტების მეთოდი.

მაგალითი 12.იპოვე ტრიგონომეტრიული ფუნქციის ინტეგრალი

.

გამოსავალი. გამოსავალი. ვისარგებლოთ უნივერსალური ტრიგონომეტრიული ჩანაცვლება. მერე
.

ვამრავლებთ მრიცხველსა და მნიშვნელში არსებულ წილადებს და ამოვიღებთ ორს და ვდებთ ინტეგრალური ნიშნის წინ. მერე

ინტეგრაციისთვის რაციონალური ფუნქციები R(sin x, cos x) სახით გამოიყენება ჩანაცვლება, რომელსაც უნივერსალური ტრიგონომეტრიული ჩანაცვლება ეწოდება. მაშინ . უნივერსალური ტრიგონომეტრიული ჩანაცვლება ხშირად იწვევს დიდ გამოთვლებს. ამიტომ, შეძლებისდაგვარად, გამოიყენეთ შემდეგი შემცვლელები.

ტრიგონომეტრიულ ფუნქციებზე რაციონალურად დამოკიდებული ფუნქციების ინტეგრაცია

1. ∫ sin n xdx , ∫ cos n xdx ფორმის ინტეგრალები, n>0
ა) თუ n კენტია, მაშინ სინქსის (ან cosx) ერთი ძალა უნდა შეიტანოს დიფერენციალური ნიშნის ქვეშ, ხოლო დარჩენილი ლუწი სიმძლავრედან გადავიდეს საპირისპირო ფუნქციაზე.
ბ) თუ n ლუწია, მაშინ ვიყენებთ ფორმულებს ხარისხის შესამცირებლად
2. ∫ tg n xdx , ∫ ctg n xdx ფორმის ინტეგრალები, სადაც n არის მთელი რიცხვი.
ფორმულები უნდა იქნას გამოყენებული

3. ∫ sin n x cos m x dx ფორმის ინტეგრალები
ა) დავუშვათ m და n განსხვავებული პარიტეტებისა. ჩვენ ვიყენებთ ჩანაცვლებას t=sin x თუ n არის კენტი ან t=cos x თუ m არის კენტი.
ბ) თუ m და n ლუწია, მაშინ ვიყენებთ ფორმულებს ხარისხის შესამცირებლად
2sin 2 x=1-cos2x, 2cos 2 x=1+cos2x.
4. ფორმის ინტეგრალები
თუ m და n რიცხვები ერთნაირი პარიტეტისაა, მაშინ ვიყენებთ ჩანაცვლებას t=tg x. ხშირად მოსახერხებელია ტრიგონომეტრიული ერთეულის ტექნიკის გამოყენება.
5. ∫ sin(nx) cos(mx)dx , ∫ cos(mx) cos(nx)dx , ∫ sin(mx) sin(nx)dx

მოდით გამოვიყენოთ ფორმულები ტრიგონომეტრიული ფუნქციების ნამრავლის ჯამად გადასაყვანად:

• sin α cos β = ½(sin(α+β)+sin(α-β))
• cos α cos β = ½(cos(α+β)+cos(α-β))
• sin α sin β = ½(cos(α-β)-cos(α+β))

მაგალითები
1. გამოთვალეთ ინტეგრალი ∫ cos 4 x·sin 3 xdx .
ვაკეთებთ ჩანაცვლებას cos(x)=t. მაშინ ∫ cos 4 x sin 3 xdx =
2. გამოთვალეთ ინტეგრალი.
ჩანაცვლების sin x=t კეთებისას მივიღებთ

3. იპოვე ინტეგრალი.
ვაკეთებთ ჩანაცვლებას tg(x)=t. ჩანაცვლება, ჩვენ ვიღებთ

R(sinx, cosx) ფორმის გამონათქვამების ინტეგრირება

მაგალითი No1. ინტეგრალების გამოთვლა:

გამოსავალი.
ა) R(sinx, cosx) ფორმის გამონათქვამების ინტეგრაცია, სადაც R არის sin x და cos x-ის რაციონალური ფუნქცია, გარდაიქმნება რაციონალური ფუნქციების ინტეგრალებში უნივერსალური ტრიგონომეტრიული ჩანაცვლების tg(x/2) = t.
მაშინ გვაქვს

უნივერსალური ტრიგონომეტრიული ჩანაცვლება შესაძლებელს ხდის ∫ R(sinx, cosx) dx ფორმის ინტეგრალიდან წილადი რაციონალური ფუნქციის ინტეგრალზე გადასვლას, მაგრამ ხშირად ასეთი ჩანაცვლება იწვევს რთულ გამონათქვამებამდე. გარკვეულ პირობებში, უფრო მარტივი ჩანაცვლება ეფექტურია:

• თუ ტოლობა R(-sin x, cos x) = -R(sin x, cos x)dx დაკმაყოფილებულია, მაშინ გამოიყენება ჩანაცვლება cos x = t.
• თუ თანასწორობა R(sin x, -cos x) = -R(sin x, cos x)dx მოქმედებს, მაშინ ჩანაცვლება sin x = t.
• თუ თანასწორობა R(-sin x, -cos x) = R(sin x, cos x)dx მოქმედებს, მაშინ ჩანაცვლება tgx = t ან ctg x = t.

ამ შემთხვევაში ინტეგრალის პოვნა
გამოვიყენოთ უნივერსალური ტრიგონომეტრიული ჩანაცვლება tg(x/2) = t.
მაშინ უპასუხე:

დეტალურად განიხილება ინტეგრალების ამონახსნების მაგალითები ნაწილების მიხედვით, რომელთა ინტეგრადი არის მრავალწევრის ნამრავლი ექსპონენციალური (e x ხარისხზე) ან სინუსზე (sin x) ან კოსინუსზე (cos x).

შინაარსი

აგრეთვე იხილეთ: ნაწილების მიერ ინტეგრაციის მეთოდი
განუსაზღვრელი ინტეგრალების ცხრილი
განუსაზღვრელი ინტეგრალების გამოთვლის მეთოდები
ძირითადი ელემენტარული ფუნქციები და მათი თვისებები

ნაწილების მიერ ინტეგრაციის ფორმულა

ამ სექციაში მაგალითების ამოხსნისას გამოიყენება ნაწილების მიერ ინტეგრაციის ფორმულა:
;
.

ინტეგრალების მაგალითები, რომლებიც შეიცავს მრავალწევრის და sin x, cos x ან e x ნამრავლს

აქ მოცემულია ასეთი ინტეგრალების მაგალითები:
, , .

ასეთი ინტეგრალების ინტეგრირებისთვის მრავალწევრი აღინიშნება u-ით, ხოლო დარჩენილი ნაწილი v dx-ით.

შემდეგი, გამოიყენეთ ინტეგრაცია ნაწილების ფორმულით. ქვემოთ მოცემულიადეტალური გადაწყვეტა

ეს მაგალითები.

ინტეგრალების ამოხსნის მაგალითები

მაგალითი მაჩვენებლით, e x-ის ხარისხზე
.

განსაზღვრეთ ინტეგრალი:
მოდით წარმოვიდგინოთ მაჩვენებლები დიფერენციალური ნიშნის ქვეშ:.

e - x dx = - e - x d(-x) = - d(e - x)

მოდით ინტეგრირება ნაწილების მიხედვით.
.
აქ
.
.
.
ჩვენ ასევე ვაერთიანებთ დარჩენილ ინტეგრალს ნაწილების მიხედვით.
.

საბოლოოდ გვაქვს:

სინუსთან ინტეგრალის განსაზღვრის მაგალითი
.

გამოთვალეთ ინტეგრალი:

e - x dx = - e - x d(-x) = - d(e - x)

მოდით შემოვიტანოთ სინუსი დიფერენციალური ნიშნის ქვეშ: აქ u = x 2, v = cos(2 x+3) ( , du = )′ x 2

dx


ჩვენ ასევე ვაერთიანებთ დარჩენილ ინტეგრალს ნაწილების მიხედვით. ამისათვის შეიტანეთ კოსინუსი დიფერენციალური ნიშნის ქვეშ. აქ u = x, v = sin (2 x+3)

ჩვენ ასევე ვაერთიანებთ დარჩენილ ინტეგრალს ნაწილების მიხედვით.

, du = dx

სინუსთან ინტეგრალის განსაზღვრის მაგალითი
.

მრავალწევრისა და კოსინუსის ნამრავლის მაგალითი

e - x dx = - e - x d(-x) = - d(e - x)

აქ u = x 2 + 3 x + 5, v = ცოდვა 2 x cos(2 x+3) ( x 2 + 3 x + 5 )′ x 2

წარმოდგენილია ძირითადი ტრიგონომეტრიული ფორმულები და ძირითადი ჩანაცვლებები. ასახულია ტრიგონომეტრიული ფუნქციების ინტეგრირების მეთოდები - რაციონალური ფუნქციების ინტეგრაცია, პროდუქტი დენის ფუნქციები sin x და cos x-დან, მრავალწევრის, ექსპონენციალური და სინუსის ან კოსინუსის ნამრავლი, შებრუნებული ტრიგონომეტრიული ფუნქციების ინტეგრაცია. გავლენას ახდენს არასტანდარტული მეთოდები.

შინაარსი

ტრიგონომეტრიული ფუნქციების ინტეგრირების სტანდარტული მეთოდები

ზოგადი მიდგომა

პირველ რიგში, საჭიროების შემთხვევაში, ინტეგრანტი უნდა გარდაიქმნას ისე, რომ ტრიგონომეტრიული ფუნქციები დამოკიდებული იყოს ერთ არგუმენტზე, რომელიც იგივეა, რაც ინტეგრაციის ცვლადი.

მაგალითად, თუ ინტეგრანტი დამოკიდებულია sin (x+a)და cos(x+b), მაშინ თქვენ უნდა შეასრულოთ კონვერტაცია:
cos (x+b) = cos (x+a - (a-b)) = cos (x+a) cos (b-a) + ცოდვა ( x+a ) ცოდვა (ბ-ა).
შემდეგ გააკეთეთ ჩანაცვლება z = x+a.

შედეგად, ტრიგონომეტრიული ფუნქციები დამოკიდებული იქნება მხოლოდ ინტეგრაციის ცვლადზე z. როდესაც ტრიგონომეტრიული ფუნქციები დამოკიდებულია ერთ არგუმენტზე, რომელიც ემთხვევა ინტეგრაციის ცვლადს (ვთქვათ ეს არის z), ანუ ინტეგრანტი შედგება მხოლოდ ისეთი ფუნქციებისგან, როგორიცაა, ცოდვა ზ, cos z, ტგ ზ ctg z
.
, მაშინ უნდა გააკეთოთ ჩანაცვლება ეს ჩანაცვლება იწვევს რაციონალური ან ირაციონალური ფუნქციების გაერთიანებას (თუ არსებობს ფესვები) და საშუალებას აძლევს გამოთვალოს ინტეგრალი, თუ ის ინტეგრირებულია.

ელემენტარული ფუნქციები

თუმცა, ხშირად შეგიძლიათ იპოვოთ სხვა მეთოდები, რომლებიც საშუალებას მოგცემთ შეაფასოთ ინტეგრალი უფრო მოკლე გზით, ინტეგრანის სპეციფიკიდან გამომდინარე. ქვემოთ მოცემულია ასეთი ძირითადი მეთოდების შეჯამება.

sin x და cos x-ის რაციონალური ფუნქციების ინტეგრირების მეთოდები რაციონალური ფუნქციებიდა ცოდვა x cos x რაციონალური ფუნქციები, ცოდვა xფუნქციები წარმოიქმნება და ნებისმიერი მუდმივი შეკრების, გამოკლების, გამრავლების, გაყოფისა და ამაღლების ოპერაციების გამოყენებით მთელ რიცხვამდე. ისინი დანიშნულნი არიან შემდეგნაირად: რ(sin x, cos x)
.
.

ეს ასევე შეიძლება მოიცავდეს ტანგენტებს და კოტანგენტებს, რადგან ისინი წარმოიქმნება სინუსის კოსინუსზე გაყოფით და პირიქით.
რაციონალური ფუნქციების ინტეგრალებს აქვთ ფორმა:
რაციონალური ტრიგონომეტრიული ფუნქციების ინტეგრირების მეთოდები შემდეგია. და ნებისმიერი მუდმივი შეკრების, გამოკლების, გამრავლების, გაყოფისა და ამაღლების ოპერაციების გამოყენებით მთელ რიცხვამდე. ისინი დანიშნულნი არიან შემდეგნაირად: რ 1) ჩანაცვლება ყოველთვის იწვევს რაციონალური წილადის ინტეგრალს. თუმცა, ზოგიერთ შემთხვევაში, არის ჩანაცვლებები (ეს მოცემულია ქვემოთ), რაც იწვევს უფრო მოკლე გამოთვლებს. რაციონალური ფუნქციები.
2) თუ რ და ნებისმიერი მუდმივი შეკრების, გამოკლების, გამრავლების, გაყოფისა და ამაღლების ოპერაციების გამოყენებით მთელ რიცხვამდე. ისინი დანიშნულნი არიან შემდეგნაირად: რ cos x → - cos x 3) თუ რგამრავლებული -1-ზე ჩანაცვლებისას ცოდვა x.
sin x → - sin x და ნებისმიერი მუდმივი შეკრების, გამოკლების, გამრავლების, გაყოფისა და ამაღლების ოპერაციების გამოყენებით მთელ რიცხვამდე. ისინი დანიშნულნი არიან შემდეგნაირად: რარ იცვლება, როგორც ერთდროული ჩანაცვლებით 1) ჩანაცვლება ყოველთვის იწვევს რაციონალური წილადის ინტეგრალს. თუმცა, ზოგიერთ შემთხვევაში, არის ჩანაცვლებები (ეს მოცემულია ქვემოთ), რაც იწვევს უფრო მოკლე გამოთვლებს., და 3) თუ რ, შემდეგ ჩანაცვლება t = tg xან t = ctg x.

მაგალითები:
, , .

cos x-ისა და sin x-ის სიმძლავრის ფუნქციების ნამრავლი

ფორმის ინტეგრალები

რაციონალური ტრიგონომეტრიული ფუნქციების ინტეგრალია. ამიტომ, წინა ნაწილში აღწერილი მეთოდები შეიძლება გამოყენებულ იქნას მათზე. ასეთი ინტეგრალების სპეციფიკაზე დაფუძნებული მეთოდები განხილულია ქვემოთ.

თუ m და n რაციონალური რიცხვებია, მაშინ ერთ-ერთი ჩანაცვლება t = რაციონალური ფუნქციებიან t = ცოდვა xინტეგრალი მცირდება დიფერენციალური ბინომის ინტეგრალამდე.

თუ m და n მთელი რიცხვებია, მაშინ ინტეგრაცია ხორციელდება შემცირების ფორმულების გამოყენებით:

;
;
;
.

მაგალითი:
.

მრავალწევრის და სინუსის ან კოსინუსის ნამრავლის ინტეგრალები

ფორმის ინტეგრალები:
, ,
სადაც P(x) არის პოლინომი x-ში, ინტეგრირებულია ნაწილებით. ეს აწარმოებს შემდეგ ფორმულებს:

;
.

მაგალითები:
, .

მრავალწევრის, ექსპონენციალური და სინუსის ან კოსინუსის ნამრავლის ინტეგრალები

ფორმის ინტეგრალები:
, ,
სადაც P(x) არის პოლინომი x-ში, ინტეგრირებული ეილერის ფორმულით
e iax = cos ცული + isin ცული(სადაც მე 2 = - 1 ).
ამისათვის, წინა აბზაცში ასახული მეთოდის გამოყენებით, გამოთვალეთ ინტეგრალი
.
რეალური და წარმოსახვითი ნაწილების შედეგისგან გამოყოფით, მიიღება ორიგინალური ინტეგრალები.

მაგალითი:
.

ტრიგონომეტრიული ფუნქციების ინტეგრირების არასტანდარტული მეთოდები

ქვემოთ მოცემულია მრავალი არასტანდარტული მეთოდი, რომელიც საშუალებას გაძლევთ შეასრულოთ ან გაამარტივოთ ტრიგონომეტრიული ფუნქციების ინტეგრაცია.

დამოკიდებულება (a sin x + b cos x)

თუ ინტეგრანტი დამოკიდებულია მხოლოდ ა sin x + b cos x, მაშინ სასარგებლოა ფორმულის გამოყენება:
,
სად .

მაგალითად

წილადების ამოხსნა სინუსებიდან და კოსინუსებიდან უფრო მარტივ წილადებად

განვიხილოთ ინტეგრალი
.
ინტეგრაციის უმარტივესი მეთოდია წილადის უფრო მარტივებად დაშლა ტრანსფორმაციის გამოყენებით:
sin(a - b) = sin(x + a - (x + b)) = sin(x+a) cos(x+b) - cos(x+a) sin(x+b)

პირველი ხარისხის წილადების ინტეგრირება

ინტეგრალის გამოთვლისას
,
მოსახერხებელია წილადის მთელი ნაწილის და მნიშვნელის წარმოებულის იზოლირება
ა 1 sin x + b 1 cos x =ა (a sin x + b cos x) +ბ (a sin x + b cos x)′ .
მუდმივები A და B გვხვდება მარცხენა და მარჯვენა გვერდების შედარებით.

გამოყენებული ლიტერატურა:
ნ.მ. გიუნტერი, რ.ო. კუზმინი, პრობლემების კრებული უმაღლესი მათემატიკა, „ლან“, 2003 წ.

აგრეთვე იხილეთ: