Sveiki! Mēs jau zinām, kas ir varbūtības sadalījums. Tas var būt diskrēts vai nepārtraukts, un mēs uzzinājām, ka to sauc par varbūtības blīvuma funkciju. varbūtības. Jo tur es iedziļināšos šajā visā sīkāk. Tā būtu varbūtība, ka mēs iegūtu tieši 2 galvas. Tagad apskatīsim dažus izplatītākus sadalījumus., jo uzskatām tos par līdzvērtīgiem.
Šeit mūs neinteresē, kura metiena rezultātā būs galvas. 5*4*3... To var pārrakstīt kā 5!/2!. ir matemātiska izteiksme, kas attēlo nejaušu mainīgo. Diskrētiem nejaušiem mainīgajiem šī matemātiskā izteiksme ir pazīstama kā sadalījuma funkcija.
Ja problēma ļauj skaidri uzrakstīt matemātisko izteiksmi, kas attēlo nejaušu mainīgo, varat aprēķināt precīzu jebkuras tā vērtības varbūtību. Šajā gadījumā varat aprēķināt un uzskaitīt visas sadalījuma funkcijas vērtības. Uzņēmējdarbības, socioloģijas un medicīnas lietojumos ir sastopami dažādi nejaušo mainīgo sadalījumi. Viens no visnoderīgākajiem sadalījumiem ir binomiāls.
Binomiālais sadalījums izmanto, lai simulētu situācijas, kuras raksturo šādas pazīmes.
- Izlase sastāv no noteikta elementu skaita n, kas atspoguļo noteikta testa rezultātus.
- Katrs parauga elements pieder vienai no divām savstarpēji izslēdzošām kategorijām, kas izsmeļ visu parauga vietu. Parasti šīs divas kategorijas sauc par panākumiem un neveiksmēm.
- Panākumu iespējamība r ir nemainīgs. Tāpēc neveiksmes varbūtība ir 1 – lpp.
- Neviena izmēģinājuma iznākums (t.i., veiksme vai neveiksme) nav atkarīgs no cita izmēģinājuma iznākuma. Lai nodrošinātu rezultātu neatkarību, izlases elementus parasti iegūst, izmantojot divas dažādas metodes. Katrs izlases elements ir nejauši iegūts no bezgalīgas populācijas bez reversijas vai no ierobežotas populācijas ar reversiju.
Lejupielādējiet piezīmi formātā vai formātā, piemērus formātā
Binomiālo sadalījumu izmanto, lai novērtētu panākumu skaitu izlasē, kas sastāv no n novērojumiem. Kā piemēru ņemsim pasūtīšanu. Lai veiktu pasūtījumu, Saxon Company klienti var izmantot interaktīvo elektronisko veidlapu un nosūtīt to uzņēmumam. Pēc tam informācijas sistēma pārbauda, vai pasūtījumos nav kļūdu, nepilnīgas vai nepareizas informācijas. Jebkurš attiecīgais pasūtījums tiek atzīmēts un iekļauts ikdienas izņēmumu pārskatā. Uzņēmuma apkopotie dati liecina, ka kļūdu iespējamība pasūtījumos ir 0,1. Uzņēmums vēlas uzzināt, kāda ir iespējamība atrast noteiktu skaitu kļūdainu pasūtījumu noteiktā paraugā. Piemēram, pieņemsim, ka klienti pabeidza četrus elektroniskās veidlapas. Kāda ir iespējamība, ka visi pasūtījumi būs bez kļūdām? Kā aprēķināt šo varbūtību? Ar panākumiem mēs sapratīsim kļūdu, aizpildot veidlapu, un visi pārējie rezultāti tiks uzskatīti par neveiksmīgiem. Atgādiniet, ka mūs interesē kļūdaino pasūtījumu skaits konkrētajā paraugā.
Kādus rezultātus mēs varam novērot? Ja paraugs sastāv no četriem pasūtījumiem, viens, divi, trīs vai visi četri var būt nepareizi, un tie visi var būt pareizi. Vai gadījuma lielums, kas apraksta nepareizi aizpildīto veidlapu skaitu, var iegūt kādu citu vērtību? Tas nav iespējams, jo nepareizo veidlapu skaits nevar pārsniegt izlases lielumu n vai būt negatīvam. Tādējādi nejaušam mainīgajam, kas pakļaujas binomiālā sadalījuma likumam, ir vērtības no 0 līdz n.
Pieņemsim, ka četru pasūtījumu izlasē tiek novēroti šādi rezultāti:
Kāda ir iespējamība atrast trīs kļūdainus pasūtījumus četru pasūtījumu izlasē norādītajā secībā? Tā kā iepriekšējie pētījumi liecina, ka kļūdas iespējamība, aizpildot veidlapu, ir 0,10, iepriekš minēto rezultātu iespējamības tiek aprēķinātas šādi:
Tā kā rezultāti nav atkarīgi viens no otra, norādītās iznākumu secības varbūtība ir vienāda ar: p*p*(1–p)*p = 0,1*0,1*0,9*0,1 = 0,0009. Ja jums ir nepieciešams aprēķināt izvēļu skaitu X n elementiem, jums jāizmanto kombinācijas formula (1):

kur n! = n * (n –1) * (n – 2) * … * 2 * 1 — skaitļa faktoriāls n, un 0! = 1 un 1! = 1 pēc definīcijas.
Šo izteicienu bieži dēvē par . Tādējādi, ja n = 4 un X = 3, secību skaitu, kas sastāv no trim elementiem, kas iegūti no parauga lieluma 4, nosaka pēc šādas formulas:
Tāpēc trīs kļūdainu pasūtījumu atklāšanas varbūtība tiek aprēķināta šādi:
(Iespējamo secību skaits) *
(konkrētas secības varbūtība) = 4 * 0,0009 = 0,0036
Līdzīgi var aprēķināt varbūtību, ka starp četriem pasūtījumiem būs viens vai divi kļūdaini, kā arī varbūtību, ka visi pasūtījumi ir kļūdaini vai visi ir pareizi. Tomēr, palielinoties izlases lielumam n kļūst grūtāk noteikt konkrētas rezultātu secības iespējamību. Šajā gadījumā jums jāpiemēro atbilstošs matemātiskais modelis, kas apraksta izvēļu skaita binomiālo sadalījumu X objekti no atlases, kas satur n elementi.
Binomiālais sadalījums

Kur P(X)- varbūtība X panākumus noteiktam izlases lielumam n un veiksmes varbūtība r, X = 0, 1, … n.
Lūdzu, ņemiet vērā, ka formula (2) ir intuitīvu secinājumu formalizācija. Nejaušs mainīgais X, kas pakļaujas binomiālajam sadalījumam, var iegūt jebkuru veselu skaitļu vērtību diapazonā no 0 līdz n. Darbs rX(1–p)n – X apzīmē konkrētas secības, kas sastāv no X panākumi izlases lielumā, kas vienāds ar n. Vērtība nosaka iespējamo kombināciju skaitu, kas sastāv no X panākumi iekšā n testiem. Tāpēc noteiktam testu skaitam n un veiksmes varbūtība r secības, kas sastāv no X panākumi, vienlīdzīgi
P(X) = (iespējamo secību skaits) * (konkrētas secības varbūtība) = 
Apskatīsim piemērus, kas ilustrē formulas (2) pielietojumu.
1. Pieņemsim, ka nepareizas veidlapas aizpildīšanas varbūtība ir 0,1. Kāda ir varbūtība, ka no četrām aizpildītajām veidlapām trīs būs nepareizas? Izmantojot formulu (2), mēs atklājam, ka trīs kļūdainu secību noteikšanas varbūtība paraugā, kas sastāv no četrām secībām, ir vienāda ar
2. Pieņemsim, ka nepareizas veidlapas aizpildīšanas varbūtība ir 0,1. Kāda ir varbūtība, ka no četrām aizpildītajām veidlapām vismaz trīs būs nepareizas? Kā parādīts iepriekšējā piemērā, varbūtība, ka no četrām aizpildītajām veidlapām trīs būs nepareizas, ir 0,0036. Lai aprēķinātu varbūtību, ka no četrām aizpildītajām veidlapām vismaz trīs būs nepareizas, jāsaskaita varbūtība, ka no četrām aizpildītajām veidlapām trīs būs nepareizas, un varbūtība, ka no četrām aizpildītajām veidlapām visas būs nepareizas. Otrā notikuma varbūtība ir
Tādējādi varbūtība, ka no četrām aizpildītajām veidlapām vismaz trīs būs nepareizas, ir vienāda ar
P(X > 3) = P(X = 3) + P(X = 4) = 0,0036 + 0,0001 = 0,0037
3. Pieņemsim, ka nepareizas veidlapas aizpildīšanas varbūtība ir 0,1. Kāda ir varbūtība, ka no četrām aizpildītajām veidlapām mazāk nekā trīs būs nepareizas? Šī notikuma varbūtība
P(X< 3) = P(X = 0) + P(X = 1) + P(X = 2)
Izmantojot formulu (2), mēs aprēķinām katru no šīm varbūtībām:

Tāpēc P(X< 3) = 0,6561 + 0,2916 + 0,0486 = 0,9963.
Varbūtība P(X< 3) можно вычислить иначе. Для этого воспользуемся тем, что событие X < 3 является дополнительным по отношению к событию Х>3. Pēc tam P(X< 3) = 1 – Р(Х> 3) = 1 – 0,0037 = 0,9963.
Pieaugot izlases lielumam n aprēķini, kas līdzīgi tiem, kas veikti 3. piemērā, kļūst sarežģīti. Lai izvairītos no šīm komplikācijām, daudzas binomiālās varbūtības ir iepriekš tabulas. Dažas no šīm varbūtībām ir parādītas attēlā. 1. Piemēram, lai iegūtu varbūtību, ka X= 2 plkst n= 4 un lpp= 0,1, no tabulas jāizņem skaitlis līnijas krustpunktā X= 2 un kolonnas r = 0,1.

Rīsi. 1. Binomiālā varbūtība pie n = 4, X= 2 un r = 0,1
Binomiālo sadalījumu var aprēķināt, izmantojot Excel funkciju =BINOM.DIST() (2. att.), kurai ir 4 parametri: veiksmes skaits - X, testu skaits (vai izlases lielums) – n, veiksmes varbūtība - r, parametrs neatņemama, kas iegūst vērtību TRUE (šajā gadījumā tiek aprēķināta varbūtība ne mazāk X notikumi) vai FALSE (šajā gadījumā tiek aprēķināta varbūtība). tieši tā X notikumi).

Rīsi. 2. Funkcijas parametri =BINOM.DIST()
Iepriekšminētajiem trim piemēriem aprēķini ir parādīti attēlā. 3 (skatiet arī Excel failu). Katrā kolonnā ir viena formula. Cipari parāda atbildes uz atbilstošā skaitļa piemēriem).

Rīsi. 3. Binomiālā sadalījuma aprēķins programmā Excel n= 4 un lpp = 0,1
Binoma sadalījuma īpašības
Binomiālais sadalījums ir atkarīgs no parametriem n Un r. Binomiālais sadalījums var būt simetrisks vai asimetrisks. Ja p = 0,05, binomiālais sadalījums ir simetrisks neatkarīgi no parametra vērtības n. Tomēr, ja p ≠ 0,05, sadalījums kļūst šķībs. Kā tuvāka vērtība parametrs r līdz 0,05 un jo lielāks ir izlases lielums n, jo mazāk izteikta sadalījuma asimetrija. Tādējādi nepareizi aizpildīto veidlapu skaita sadalījums ir šķībs uz labo pusi, jo lpp= 0,1 (4. att.).

Rīsi. 4. Binomiālā sadalījuma histogramma plkst n= 4 un lpp = 0,1
Binomiālā sadalījuma sagaidāmais vienāds ar izlases lieluma reizinājumu n par veiksmes varbūtību r:
(3) M = E(X) =n.p.
Vidēji ar pietiekami garu testu sēriju izlasē, kas sastāv no četriem pasūtījumiem, var būt p = E(X) = 4 x 0,1 = 0,4 nepareizi aizpildītas veidlapas.
Binoma sadalījuma standartnovirze
Piemēram, standarta novirze nepareizi aizpildītu veidlapu skaits grāmatvedībā informācijas sistēma vienāds:
Izmantoti materiāli no grāmatas Levin et al. Statistika vadītājiem. – M.: Williams, 2004. – lpp. 307–313
Ne visas parādības tiek mērītas kvantitatīvā skalā, piemēram, 1, 2, 3... 100500... Parādība ne vienmēr var iegūt bezgalīgu vai lielu skaitu dažādu stāvokļu. Piemēram, personas dzimums var būt vai nu M, vai F. Šāvējs vai nu trāpa mērķī, vai netrāpa. Balsot var “Par” vai “Pret” utt. utt. Citiem vārdiem sakot, šādi dati atspoguļo alternatīvā atribūta stāvokli - vai nu “jā” (notikums notika) vai “nē” (notikums nenotika). Notiekošo notikumu (pozitīvo iznākumu) sauc arī par “veiksmi”.
Eksperimenti ar šādiem datiem tiek saukti Bernulli shēma, par godu slavenajam Šveices matemātiķim, kurš atklāja, ka ar lielu skaitu izmēģinājumu pozitīvo iznākumu attiecība pret kopējo izmēģinājumu skaitu ir tendence uz šī notikuma rašanās varbūtību.
Alternatīvs raksturlielums
Lai analīzē izmantotu matemātisko aparātu, šādu novērojumu rezultāti jāreģistrē skaitliskā forma. Lai to izdarītu, pozitīvam iznākumam tiek piešķirts skaitlis 1, negatīvam - 0. Citiem vārdiem sakot, mums ir darīšana ar mainīgo, kam var būt tikai divas vērtības: 0 vai 1.
Kādu labumu no tā var gūt? Patiesībā ne mazāk kā no parastajiem datiem. Tādējādi ir viegli aprēķināt pozitīvo iznākumu skaitu - vienkārši summējiet visas vērtības, t.i. visi 1 (veiksmīgi). Jūs varat iet tālāk, taču jums būs jāievieš pāris apzīmējumi.
Vispirms jāatzīmē, ka pozitīviem rezultātiem (kas ir vienādi ar 1) ir zināma iespējamība, ka tie notiks. Piemēram, galviņu iegūšana, metot monētu, ir ½ vai 0,5. Šo varbūtību tradicionāli apzīmē ar latīņu burtu lpp. Tāpēc alternatīva notikuma iespējamība ir vienāda ar 1. lpp, ko arī apzīmē ar q, tas ir q = 1 – p. Šos apzīmējumus var skaidri sistematizēt mainīgo sadalījuma tabulas veidā X.
Mēs saņēmām iespējamo vērtību un to varbūtību sarakstu. Var aprēķināt matemātiskās cerības Un dispersija. Paredzētais ir visu iespējamo vērtību un to atbilstošo varbūtību produktu summa:
![]()
Aprēķināsim paredzamo vērtību, izmantojot apzīmējumus augstāk esošajās tabulās.
Izrādās, ka alternatīvas zīmes matemātiskā cerība ir vienāda ar šī notikuma varbūtību - lpp.
Tagad definēsim, kāda ir alternatīvā atribūta dispersija. Izkliede ir vidējais kvadrāts novirzēm no matemātiskās cerības. Vispārējā formula(diskrētiem datiem) ir šāda forma:
Tādējādi alternatīvā atribūta dispersija:

Ir viegli redzēt, ka šīs dispersijas maksimums ir 0,25 (ar p=0,5).
Standarta novirze ir dispersijas sakne:
Maksimālā vērtība nepārsniedz 0,5.
Kā redzat, gan matemātiskajai cerībai, gan alternatīvā atribūta dispersijai ir ļoti kompakta forma.
Gadījuma lieluma binomālais sadalījums
Paskatīsimies uz situāciju no cita leņķa. Patiešām, kuru interesē tas, ka vidējais galvu zudums uz vienu metienu ir 0,5? Nav iespējams pat iedomāties. Interesantāk ir uzdot jautājumu par galvu skaitu, kas rodas noteiktam metienu skaitam.
Citiem vārdiem sakot, pētnieku bieži interesē noteikta skaita veiksmīgu notikumu varbūtība. Tas var būt bojāto produktu skaits pārbaudītajā partijā (1 - bojāts, 0 - labs) vai atgūto produktu skaits (1 - vesels, 0 - slims) utt. Šādu “veiksmju” skaits būs vienāds ar visu mainīgā lieluma vērtību summu X, t.i. atsevišķu rezultātu skaits.
Nejaušs mainīgais B sauc par binomiālu un ņem vērtības no 0 līdz n(pie B= 0 – visas daļas ir piemērotas, ar B = n– visas detaļas ir bojātas). Tiek pieņemts, ka visas vērtības x neatkarīgi viens no otra. Apskatīsim binoma mainīgā galvenās īpašības, tas ir, mēs noteiksim tā matemātisko cerību, izkliedi un sadalījumu.
Binoma mainīgā lieluma gaidīšanu ir ļoti viegli iegūt. Daudzumu summas matemātiskā cerība ir katra pievienotā daudzuma matemātisko gaidu summa, un tā ir vienāda visiem, tāpēc:
Piemēram, 100 metienos nomesto galvu matemātiskā prognoze ir 100 × 0,5 = 50.
Tagad mēs iegūstam binoma mainīgā izkliedes formulu. Neatkarīgo gadījuma lielumu summas dispersija ir dispersiju summa. No šejienes
Attiecīgi standarta novirze
100 monētu mešanām galviņu skaita standartnovirze ir
Visbeidzot, apsveriet binoma vērtības sadalījumu, t.i. varbūtība, ka nejaušais mainīgais B iegūs dažādas vērtības k, Kur 0≤k≤n. Monētai šī problēma varētu izskatīties šādi: Kāda ir varbūtība, ka uz 100 metieniem tiks iegūtas 40 galvas?
Lai saprastu aprēķina metodi, iedomājieties, ka monēta tiek izmesta tikai 4 reizes. Katra puse var izkrist katru reizi. Jautājam sev: kāda ir varbūtība iegūt 2 galvas no 4 metieniem. Katrs metiens ir neatkarīgs viens no otra. Tas nozīmē, ka varbūtība iegūt jebkuru kombināciju būs vienāda ar dotā iznākuma varbūtību reizinājumu katram atsevišķam metienam. Lai O ir galvas, P ir astes. Tad, piemēram, viena no mums piemērotajām kombinācijām var izskatīties kā OOPP, tas ir:

Šādas kombinācijas iespējamība ir vienāda ar divu varbūtību iegūt galvu un vēl divām varbūtību nesaņemt galvu reizinājumu (apgrieztais notikums, kas aprēķināts kā 1. lpp), t.i. 0,5 × 0,5 × (1–0,5) × (1–0,5) = 0,0625. Tāda ir vienas no mums piemērotas kombinācijas varbūtība. Bet jautājums bija par kopējo ērgļu skaitu, nevis par kādu konkrētu kārtību. Tad jums ir jāsaskaita visu to kombināciju varbūtības, kurās ir tieši 2 galvas. Skaidrs, ka tie visi ir vienādi (produkts nemainās, mainot faktorus). Tāpēc jums ir jāaprēķina to skaits un pēc tam jāreizina ar šādas kombinācijas varbūtību. Saskaitīsim visas 4 metienu kombinācijas pa 2 galvām: RROO, RORO, ROOR, ORRO, OROR, OORR. Kopumā ir 6 iespējas.

Līdz ar to vēlamā iespējamība tikt pie 2 galvām pēc 4 metieniem ir 6×0,0625=0,375.
Tomēr skaitīt šādā veidā ir nogurdinoši. Jau 10 monētām ar brutālu spēku iegūt kopējo opciju skaitu būs ļoti grūti. Tieši tāpēc gudri cilvēki sen izgudroja formulu, ar kuras palīdzību var aprēķināt dažādu kombināciju skaitu n elementi no k, Kur n- kopējais elementu skaits, k– elementu skaits, kuru izkārtojuma iespējas tiek aprēķinātas. Formulas kombinācija n elementi no k vai šis:
![]()
Līdzīgas lietas notiek kombinatorikas sadaļā. Sūtu tur ikvienu, kurš vēlas papildināt savas zināšanas. Līdz ar to, starp citu, arī binoma sadalījuma nosaukums (iepriekš minētā formula ir Ņūtona binoma izplešanās koeficients).
Varbūtības noteikšanas formulu var viegli vispārināt uz jebkuru lielumu n Un k. Rezultātā binomiālā sadalījuma formulai ir šāda forma.
Nosacījumam atbilstošo kombināciju skaits tiek reizināts ar vienas no tām varbūtību.
Praktiskai lietošanai pietiek tikai zināt binomiālā sadalījuma formulu. Vai arī jūs, iespējams, pat nezināt - zemāk mēs parādīsim, kā noteikt varbūtību, izmantojot Excel. Bet labāk ir zināt.
Izmantojot šo formulu, mēs aprēķinām varbūtību iegūt 40 galvas 100 metienos:
Vai tikai 1,08%. Salīdzinājumam, šī eksperimenta matemātiskās cerības, tas ir, 50 galvas, varbūtība ir vienāda ar 7,96%. Binoma vērtības maksimālā varbūtība pieder vērtībai, kas atbilst matemātiskajai cerībai.
Binoma sadalījuma varbūtības aprēķināšana programmā Excel
Ja izmantojat tikai papīru un kalkulatoru, tad aprēķini, izmantojot binominālā sadalījuma formulu, neskatoties uz to, ka nav integrāļu, ir diezgan sarežģīti. Piemēram, vērtība ir 100! - ir vairāk nekā 150 rakstzīmes. Iepriekš un arī tagad šādu daudzumu aprēķināšanai tika izmantotas aptuvenas formulas. Šobrīd vēlams izmantot speciālu programmatūru, piemēram, MS Excel. Tādējādi jebkurš lietotājs (pat humānists pēc apmācības) var viegli aprēķināt binomiāli sadalīta gadījuma lieluma vērtības varbūtību.
Materiāla konsolidācijai pagaidām izmantosim Excel kā parastu kalkulatoru, t.i. Veiksim soli pa solim aprēķinu, izmantojot binomiālā sadalījuma formulu. Aprēķināsim, piemēram, varbūtību iegūt 50 galvas. Zemāk ir attēls ar aprēķina soļiem un gala rezultātu.

Kā redzat, starprezultāti ir tāda mēroga, ka tie neietilpst šūnā, lai gan tiek izmantoti visur vienkāršas funkcijas veidi: FACTOR (faktoriāla aprēķins), JAUDA (skaitļa paaugstināšana pakāpē), kā arī reizināšanas un dalīšanas operatori. Turklāt šis aprēķins ir diezgan apgrūtinošs, tas nav kompakts, jo ir iesaistītas daudzas šūnas. Jā, un to ir nedaudz grūti izdomāt uzreiz.
Kopumā Excel nodrošina gatavu funkciju binoma sadalījuma varbūtību aprēķināšanai. Funkcija tiek izsaukta BINOM.DIST.

Panākumu skaits – veiksmīgo testu skaits. Mums ir 50 no tiem.
Pārbaužu skaits – metienu skaits: 100 reizes.
Panākumu iespējamība – iespēja dabūt galvas vienā metienā ir 0,5.
Integrāls – ir norādīts 1 vai 0 Ja 0, tad tiek aprēķināta varbūtība P(B=k); ja 1, tad tiks aprēķināta binomiālā sadalījuma funkcija, t.i. visu varbūtību summa no B=0 uz B=k ieskaitot.
Noklikšķiniet uz Labi un iegūstiet tādu pašu rezultātu kā iepriekš, tikai viss tika aprēķināts ar vienu funkciju.

Ļoti ērti. Eksperimentu labad pēdējā parametra 0 vietā liekam 1. Iegūstam 0,5398. Tas nozīmē, ka, izmetot 100 monētas, varbūtība iegūt galviņas no 0 līdz 50 ir gandrīz 54%. Bet sākumā likās, ka vajadzētu būt 50%. Kopumā aprēķini tiek veikti ātri un vienkārši.
Īstam analītiķim ir jāsaprot, kā funkcija darbojas (kāds ir tās sadalījums), tāpēc mēs aprēķināsim varbūtības visām vērtībām no 0 līdz 100. Tas ir, mēs uzdosim jautājumu: kāda ir varbūtība, ka neviens ērglis parādīsies, ka parādīsies 1 ērglis, 2, 3 , 50, 90 vai 100. Aprēķins parādīts nākamajā attēlā. Zilā līnija ir pats binomiālais sadalījums, sarkanais punkts ir noteikta veiksmes skaita k varbūtība.

Varētu jautāt, vai binomiālais sadalījums ir līdzīgs... Jā, ļoti līdzīgs. Pat Moivre (1733. gadā) teica, ka tuvojas binomiālais sadalījums ar lieliem paraugiem (nezinu, kā toreiz to sauca), bet neviens viņā neklausījās. Tikai Gauss un pēc 60–70 gadiem Laplass tika atklāti no jauna un rūpīgi izpētīti normāls likums sadales. Iepriekš redzamais grafiks skaidri parāda, ka maksimālā varbūtība attiecas uz matemātisko cerību, un, tai novirzoties no tās, tā strauji samazinās. Tāpat kā parastais likums.
Binomiālajam sadalījumam ir liels praktiska nozīme, notiek diezgan bieži. Izmantojot programmu Excel, aprēķini tiek veikti ātri un vienkārši.
Apskatīsim Bernulli shēmas ieviešanu, t.i. Tiek veikta virkne atkārtotu neatkarīgu testu, kuros katrā konkrētajam notikumam A ir tāda pati varbūtība neatkarīgi no testa numura. Un katram testam ir tikai divi rezultāti:
1) pasākums A - veiksme;
2) notikums - neveiksme,
ar pastāvīgām varbūtībām
Ņemsim vērā diskrētu gadījuma lielumu X - “notikuma A gadījumu skaits plkst n testi" un atrodiet šī gadījuma lieluma sadalījuma likumu. Vērtībai X var būt šādas vērtības:
Varbūtība ![]() ka nejaušais lielums X pieņems vērtību x k atrasts pēc Bernulli formulas
ka nejaušais lielums X pieņems vērtību x k atrasts pēc Bernulli formulas
Tiek izsaukts diskrēta gadījuma lieluma sadalījuma likums, kas definēts ar Bernulli formulu (1). Binomiālā sadalījuma likums. Pastāvīgs n Un r (q=1-p), kas iekļauti formulā (1), tiek saukti binomiālā sadalījuma parametri.
Nosaukums “binomiālais sadalījums” ir saistīts ar faktu, ka labā puse vienādībā (1) ir Ņūtona binoma izplešanās vispārīgais termins, t.i.
(2)
Un kopš tā laika p+q=1, tad vienādības (2) labā puse ir vienāda ar 1
Tas nozīmē, ka
 (4)
(4)
Vienlīdzībā (3) pirmais termiņš qn labajā pusē nozīmē varbūtību, ka iekšā n testi, notikums A neparādīsies pat vienu reizi, otrais termiņš ![]() varbūtība, ka notikums A parādīsies vienu reizi, trešais termins ir varbūtība, ka notikums A parādīsies divreiz, un visbeidzot pēdējais termins r p- varbūtība, ka notikums A notiks precīzi n vienreiz.
varbūtība, ka notikums A parādīsies vienu reizi, trešais termins ir varbūtība, ka notikums A parādīsies divreiz, un visbeidzot pēdējais termins r p- varbūtība, ka notikums A notiks precīzi n vienreiz.
Diskrētā gadījuma lieluma sadalījuma binomiālais likums ir parādīts tabulas veidā:
| X | 0 | 1 | … | k | … | n |
| R | qn | … | … | r p |
Pamata skaitliskās īpašības Binomiālais sadalījums:
1) matemātiskās cerības ![]() (5)
(5)
2) dispersija ![]() (6)
(6)
3) standarta novirze ![]() (7)
(7)
4) visticamākais notikuma atgadījumu skaits k 0- šis ir skaitlis, kas dotajam n atbilst maksimālajai binoma varbūtībai
Par doto n Un ršo skaitli nosaka nevienādības
![]() (8)
(8)
ja numurs pr+r tad nav vesels k 0 vienāds ar šī skaitļa veselo daļu, ja pr+r tad ir vesels skaitlis k 0 ir divas nozīmes
Binomiālais varbūtības sadalījuma likums tiek izmantots šaušanas teorijā, statistikas produktu kvalitātes kontroles teorijā un praksē, rindu teorijā, uzticamības teorijā u.c. Šo likumu var piemērot visos gadījumos, kad ir neatkarīgu testu secība.
1. piemērs: Kvalitātes pārbaude atklāja, ka no katrām 100 ierīcēm vidēji 90 ir bez defektiem. Izveidojiet nejauši iegādāto augstas kvalitātes ierīču skaita varbūtības sadalījuma binomiālo likumu 4.
Risinājums: Notikums A, kura iestāšanās tiek pārbaudīta, ir “nejauši iegādāta augstas kvalitātes ierīce”. Atbilstoši problēmas nosacījumiem galvenie binomiālā sadalījuma parametri ir:
Nejaušais lielums X ir augstas kvalitātes ierīču skaits no 4, kas nozīmē X vērtības - Ļaujiet mums atrast X vērtību varbūtības, izmantojot formulu (1):

Tādējādi vērtības X sadalījuma likums ir augstas kvalitātes ierīču skaits no 4:
| X | 0 | 1 | 2 | 3 | 4 |
| R | 0,0001 | 0,0036 | 0,0486 | 0,2916 | 0,6561 |
Lai pārbaudītu sadalījuma uzbūves pareizību, pārbaudīsim, kāda varbūtību summa ir vienāda ar
Atbilde: Sadales likums
| X | 0 | 1 | 2 | 3 | 4 |
| R | 0,0001 | 0,0036 | 0,0486 | 0,2916 | 0,6561 |
2. piemērs: Izmantotā ārstēšanas metode noved pie atveseļošanās 95% gadījumu. Šo metodi izmantoja pieci pacienti. Atrodiet visticamāko atveseļojošo cilvēku skaitu, kā arī nejaušā lieluma X skaitliskos raksturlielumus - atveseļojušos cilvēku skaitu no 5 pacientiem, kuri izmantoja šo metodi.
Binomiālais sadalījums ir viens no svarīgākajiem diskrēti mainīga gadījuma lieluma varbūtības sadalījumiem. Binomiālais sadalījums ir skaitļa varbūtības sadalījums m notikuma rašanos A V n savstarpēji neatkarīgi novērojumi. Bieži vien pasākums A tiek saukts par novērojuma “veiksmi”, un pretējo notikumu sauc par “neveiksmi”, taču šis apzīmējums ir ļoti nosacīts.
Binomiālā sadalījuma nosacījumi:
- kopumā veikta n izmēģinājumi, kuros pasākums A var notikt vai nenotikt;
- notikumu A katrā izmēģinājumā var notikt ar tādu pašu varbūtību lpp;
- testi ir savstarpēji neatkarīgi.
Varbūtība, ka in n pārbaudes pasākums A tas pienāks tieši m reizes, var aprēķināt, izmantojot Bernulli formulu:
![]()
Kur lpp- notikuma varbūtība A;
q = 1 - lpp- pretēja notikuma varbūtība.
Izdomāsim kāpēc binomālais sadalījums ir saistīts ar Bernulli formulu iepriekš aprakstītajā veidā? . Pasākums – panākumu skaits plkst n testi ir sadalīti vairākās opcijās, no kurām katrā tiek gūti panākumi m testi, un neveiksme - in n - m testiem. Apsvērsim vienu no šīm iespējām - B1 . Izmantojot varbūtību saskaitīšanas noteikumu, mēs reizinām pretēju notikumu varbūtības:
![]() ,
,
un ja apzīmējam q = 1 - lpp, Tas
![]() .
.
Jebkurš cits variants, kurā m panākumi un n - m neveiksmēm. Šādu iespēju skaits ir vienāds ar iespēju skaitu n pārbaudi iegūt m panākumus.
Visu varbūtību summa m notikumu iestāšanās numuri A(skaitļi no 0 līdz n) ir vienāds ar vienu:

kur katrs termins apzīmē Ņūtona binoma vārdu. Tāpēc aplūkojamo sadalījumu sauc par binomiālo sadalījumu.
Praksē bieži vien ir nepieciešams aprēķināt varbūtības "ne vairāk kā m panākumi iekšā n testi" vai "vismaz m panākumi iekšā n testi". Šim nolūkam tiek izmantotas šādas formulas.
Integrālā funkcija, tas ir varbūtība F(m) kas ir iekšā n novērošanas pasākums A vairāk nenāks m vienreiz, var aprēķināt, izmantojot formulu:
Savukārt varbūtība F(≥m) kas ir iekšā n novērošanas pasākums A nāks ne mazāk m vienreiz, aprēķina pēc formulas:
Dažreiz ir ērtāk aprēķināt varbūtību, ka n novērošanas pasākums A vairāk nenāks m reizes, izmantojot pretēja notikuma varbūtību:
![]() .
.
Izmantojamā formula ir atkarīga no tā, kurā no tām ir summa, kurā ir mazāk terminu.
Binoma sadalījuma raksturlielumus aprēķina, izmantojot šādas formulas .
Matemātiskās cerības: .
Izkliede:.
Binomiālais sadalījums un aprēķini programmā MS Excel
Binomiālā varbūtība P n ( m) un integrālās funkcijas vērtības F(m) var aprēķināt, izmantojot MS Excel funkciju BINOM.DIST. Attiecīgā aprēķina logs ir parādīts zemāk (kreisais klikšķis, lai palielinātu).

Programmai MS Excel ir jāievada šādi dati:
- panākumu skaits;
- pārbaužu skaits;
- veiksmes varbūtība;
- neatņemama - Būla vērtība: 0 - ja nepieciešams aprēķināt varbūtību P n ( m) un 1 - ja varbūtība F(m).
1. piemērs. Uzņēmuma vadītājs apkopoja informāciju par pēdējo 100 dienu laikā pārdoto kameru skaitu. Tabulā apkopota informācija un aprēķināta varbūtība, ka dienā tiks pārdots noteikts skaits kameru.
Diena beidzas ar peļņu, ja tiek pārdotas 13 vai vairāk kameras. Varbūtība, ka diena būs izdevīga:
![]()
Varbūtība, ka diena tiks nostrādāta bez peļņas:
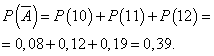
Lai varbūtība, ka diena tiek nostrādāta ar peļņu, ir nemainīga un vienāda ar 0,61, un dienā pārdoto kameru skaits nav atkarīgs no dienas. Tad mēs varam izmantot binomiālo sadalījumu, kur notikums A- diena tiks nostrādāta ar peļņu, - bez peļņas.
Varbūtība, ka visas 6 dienas tiks nostrādātas ar peļņu:
![]() .
.
To pašu rezultātu iegūstam, izmantojot MS Excel funkciju BINOM.DIST (integrāļa vērtības vērtība ir 0):
P 6 (6 ) = BINOM.DIST(6; 6; 0,61; 0) = 0,052.
Varbūtība, ka no 6 dienām 4 vai vairāk dienas tiks nostrādātas ar peļņu:
Kur ![]() ,
,
![]() ,
,
Izmantojot MS Excel funkciju BINOM.DIST, mēs aprēķinām varbūtību, ka no 6 dienām ne vairāk kā 3 dienas tiks pabeigtas ar peļņu (integrālās vērtības vērtība ir 1):
P 6 (≤3 ) = BINOM.DALĪJUMS(3; 6; 0,61; 1) = 0,435.
Varbūtība, ka visas 6 dienas tiks nostrādātas ar zaudējumiem:
![]() ,
,
To pašu rādītāju varam aprēķināt, izmantojot MS Excel funkciju BINOM.DIST:
P 6 (0 ) = BINOM.DALĪJUMS(0; 6; 0,61; 0) = 0,0035.
Atrisiniet problēmu pats un tad skatiet risinājumu
2. piemērs. Urnā ir 2 baltas un 3 melnas bumbiņas. No urnas izņem bumbiņu, nosaka krāsu un noliek atpakaļ. Mēģinājums tiek atkārtots 5 reizes. Balto bumbiņu gadījumu skaits ir diskrēts gadījuma lielums X, sadalīts saskaņā ar binominālo likumu. Sastādiet nejauša lieluma sadalījuma likumu. Definējiet režīmu, matemātisko cerību un izkliedi.
Turpināsim kopīgi risināt problēmas
3. piemērs. No kurjera dienesta devāmies uz vietām n= 5 kurjeri. Visticamāk, katrs kurjers lpp= 0,3, neatkarīgi no citiem, objektam kavējas. Diskrēts nejaušības lielums X- kavēto kurjeru skaits. Izveidojiet sadalījuma sēriju šim nejaušajam mainīgajam. Atrodiet tā matemātisko cerību, dispersiju, standarta novirzi. Atrodiet varbūtību, ka vismaz divi kurjeri kavēs pie objektiem.