Гэр

Функцийн график хэдэн асимптоттой байж болох вэ? Нэг, нэг, хоёр, гурав,... эсвэл хязгааргүй олон биш. Бид жишээн дээр хол явахгүй, энгийн функцуудыг санацгаая. Парабол, куб парабол, синусын долгионд асимптот огт байдаггүй. экспоненциал график,логарифм функц

өвөрмөц асимптоттой. Арктангенс ба арккотангенс нь хоёртой, тангенс ба котангенс нь хязгааргүй олонтой. График нь хэвтээ ба босоо асимптоттой байх нь ердийн зүйл биш юм. Гипербол, чамайг үргэлж хайрлах болно.

Функцийн графикийн асимптотуудыг олно гэдэг нь юу гэсэн үг вэ?

Энэ нь тэдгээрийн тэгшитгэлийг олох, хэрэв асуудал шаардлагатай бол шулуун шугам зурах гэсэн үг юм. Үйл явц нь функцийн хязгаарыг олох явдал юм.

Функцийн графикийн босоо асимптотууд

Графикийн босоо асимптот нь дүрмээр бол функцийн хязгааргүй тасалдлын цэг дээр байрладаг. Энэ нь энгийн: хэрэв тухайн цэг дээр функц хязгааргүй тасалдалтай байвал тэгшитгэлээр тодорхойлсон шулуун шугам нь графикийн босоо асимптот болно.

Жич: Энэ оруулга нь огт өөр хоёр ойлголтыг илэрхийлэхэд ашиглагдаж байгааг анхаарна уу. Цэг нь далдлагдсан эсвэл шулууны тэгшитгэл байх нь контекстээс хамаарна.

Тиймээс нэг цэгт босоо асимптот байгаа эсэхийг тогтоохын тулд ядаж нэг талт хязгаарын нэг нь хязгааргүй гэдгийг харуулахад хангалттай. Ихэнхдээ энэ нь функцийн хуваагч тэг байх цэг юм. Үндсэндээ бид функцийн тасралтгүй байдлын тухай хичээлийн сүүлийн жишээнүүдээс босоо асимптотуудыг аль хэдийн олсон. Гэхдээ зарим тохиолдолд зөвхөн нэг талын хязгаар байдаг бөгөөд хэрэв энэ нь хязгааргүй бол дахин босоо асимптотыг хайрлаж, илүүд үздэг. Хамгийн энгийн дүрслэл: ординатын тэнхлэг.

Дээрхээс харахад тодорхой баримт гарч ирнэ: хэрэв функц тасралтгүй ажиллаж байвал босоо асимптот байхгүй болно. Яагаад ч юм парабола санаанд орж ирэв. Үнэхээр энд шулуун шугамыг хаана “наах” вэ? ...тиймээ... би ойлголоо... Фрейдийн авга дагалдагчид гстерик байсан =)

Эсрэг заалт нь ерөнхийдөө худал байдаг: жишээлбэл, функц нь бүх тооны мөрөнд тодорхойлогдоогүй, харин асимптотоос бүрэн хасагдсан байдаг.

Хэрэв функцийн аргумент нь "нэмэх хязгааргүй" эсвэл "хасах хязгааргүй" хандлагатай байвал ташуу (тусгай тохиолдолд - хэвтээ) асимптотуудыг зурж болно. Иймд функцийн график нь 2-оос илүү налуу асимптоттой байж болохгүй. Жишээлбэл, экспоненциал функцийн график нь нэг хэвтээ асимптоттой, at арктангенсын график нь хоёр ийм асимптоттой, өөр өөр байдаг.

Хоёр газрын график нь нэг ташуу асимптот руу ойртох үед "хязгааргүй" -ийг нэг оруулгын дор нэгтгэдэг заншилтай байдаг. Жишээлбэл, ... та зөв таасан: .

Функцийн графикийн асимптотууд

Асимптотын сүнс эцэст нь тусдаа нийтлэлд тусгагдахын тулд сайтыг тойрон удаан хугацаанд тэнүүчилж, гайхширсан уншигчдад онцгой таашаал авчирсан. функцийг бүрэн судлах. Графикийн асимптотуудыг олох нь энэ ажлын цөөн хэдэн хэсгүүдийн нэг юм сургуулийн курсҮйл явдал нь тооцоололд эргэлддэг тул зөвхөн тоймоор функцийн хязгаарлалт, гэхдээ тэдгээр нь дээд математикт харьяалагддаг хэвээр байна. Математик анализын талаар багахан ойлголттой зочдод зориулсан зөвлөгөө нь ойлгомжтой гэж бодож байна ;-) ...зогс, зогсоо, хаашаа явах гэж байна? Хязгаарлалт- амархан!

Асимптотуудын жишээг анхны хичээл дээр шууд олж мэдсэн энгийн функцүүдийн графикууд, мөн уг сэдвийг одоо нарийвчлан авч үзэж байна.

Тэгэхээр асимптот гэж юу вэ?

Төсөөлөөд үз дээ хувьсах цэг, энэ нь функцийн графикийн дагуу "аялж" байна. Асимптот нь шулуун, аль нь хязгааргүй ойрхонХэрэв та үүнийг арилгах үед функцийн график ойртож байна хувьсах цэгхязгааргүй хүртэл.

Анхаарна уу : Тодорхойлолт нь утга учиртай, хэрэв танд тооцооллын тэмдэглэгээний томъёолол хэрэгтэй бол сурах бичгээс үзнэ үү.

Онгоцонд асимптотуудыг байгалийн байршлаар нь ангилдаг.

1) Босоо асимптотууд, "альфа" нь бодит тоо гэсэн хэлбэрийн тэгшитгэлээр өгөгдсөн. Алдартай төлөөлөгч нь ордны тэнхлэгийг өөрөө тодорхойлдог.
бага зэрэг дотор муухайрах мэдрэмжээр бид гиперболыг санаж байна.

2) Ташуу асимптотуудуламжлал ёсоор бичсэн шулуун шугамын тэгшитгэлөнцгийн коэффициенттэй. Заримдаа онцгой тохиолдлыг тусдаа бүлэг болгон тодорхойлдог. хэвтээ асимптотууд. Жишээлбэл, асимптоттой ижил гипербол.

Хурдан явцгаая, сэдвийг богино хугацаанд пулемётоор буудъя:

Функцийн график хэдэн асимптоттой байж болох вэ?

Нэг, нэг, хоёр, гурав,... эсвэл хязгааргүй олон биш. Бид жишээ авах гэж хол явахгүй, санацгаая үндсэн функцууд. Парабол, куб парабол, синусын долгионд асимптот огт байдаггүй. Экспоненциал, логарифм функцийн график нь нэг асимптоттой. Арктангенс ба арккотангенс нь хоёртой, тангенс ба котангенс нь хязгааргүй олонтой. График нь хэвтээ ба босоо асимптоттой байх нь ердийн зүйл биш юм. Гипербол, чамайг үргэлж хайрлах болно.

Энэ нь юу гэсэн үг вэ?

Функцийн графикийн босоо асимптотууд

Графикийн босоо асимптот нь ихэвчлэн байрладаг хязгааргүй тасрах цэг дээрфункцууд. Энэ нь энгийн: хэрэв тухайн цэг дээр функц хязгааргүй тасалдалтай байвал тэгшитгэлээр тодорхойлсон шулуун шугам нь графикийн босоо асимптот болно.

Анхаарна уу : Бичлэг нь огт өөр хоёр ойлголтыг илэрхийлэхэд ашиглагдаж байгааг анхаарна уу. Цэг нь далдлагдсан эсвэл шулууны тэгшитгэл байх нь контекстээс хамаарна.

Тиймээс нэг цэгт босоо асимптот байгаа эсэхийг тогтоохын тулд үүнийг харуулахад хангалттай ядаж нэгнэг талын хязгаараас хязгааргүй. Ихэнхдээ энэ нь функцийн хуваагч тэг байх цэг юм. Үндсэндээ бид хичээлийн сүүлийн жишээн дээр босоо асимптотуудыг аль хэдийн олсон функцийн тасралтгүй байдлын тухай. Гэхдээ зарим тохиолдолд зөвхөн нэг талын хязгаар байдаг бөгөөд хэрэв энэ нь хязгааргүй бол дахин босоо асимптотыг хайрлаж, илүүд үздэг. Хамгийн энгийн дүрслэл: ординатын тэнхлэг (харна уу. Энгийн функцүүдийн график ба шинж чанарууд).

Дээр дурдсанаас харахад тодорхой баримт дараах байдалтай байна. хэрэв функц тасралтгүй асаалттай байвал, тэгвэл босоо асимптот байхгүй болно. Яагаад ч юм нэг парабол санаанд орж ирэв. Үнэхээр энд шулуун шугамыг хаана “наах” вэ? ...тиймээ... би ойлголоо... Фрейдийн авга дагалдагчид гстерик байсан =)

Функцийн графикийн налуу асимптотууд

Хэрэв функцийн аргумент нь "нэмэх хязгааргүй" эсвэл "хасах хязгааргүй" хандлагатай байвал ташуу (тусгай тохиолдолд - хэвтээ) асимптотуудыг зурж болно. Тийм ч учраас Функцийн график нь хоёроос илүү налуу асимптоттой байж болохгүй. Жишээ нь, экспоненциал функцийн график нь -д нэг хэвтээ асимптоттой, харин арктангенсын график нь хоёр ийм асимптоттой, өөр өөр байдаг.

Хоёр газрын график нь нэг ташуу асимптот руу ойртох үед "хязгааргүй" нь ихэвчлэн нэг бичилт дор нэгтгэгддэг. Жишээлбэл, ... та зөв таасан: .

Генерал дүрэм :

Хэрэв хоёр байвал эцсийнхязгаар , тэгвэл шулуун шугам нь функцийн графикийн ташуу асимптот болно. Хэрэв ядаж нэгжагсаасан хязгаарын хязгаар нь хязгааргүй, тэгвэл ташуу асимптот байхгүй болно.

Анхаарна уу : "x" нь зөвхөн "нэмэх хязгааргүй" эсвэл зөвхөн "хасах хязгааргүй" хандлагатай байвал томъёонууд хүчинтэй хэвээр байна.

Параболд ташуу асимптот байхгүй гэдгийг харуулъя.

Хязгаар нь хязгааргүй бөгөөд энэ нь ташуу асимптот байхгүй гэсэн үг юм. Хязгаарыг олохдоо үүнийг анхаарна уу Хариулт нь аль хэдийн ирсэн тул хэрэгцээ алга болсон.

Анхаарна уу : Хэрэв танд нэмэх-хасах, хасах-нэмэх тэмдгийг ойлгоход бэрхшээлтэй байгаа бол (эсвэл тулгарах болно) хичээлийн эхэнд байгаа тусламжийг үзнэ үү.
хязгааргүй жижиг функцууд дээр, Би эдгээр тэмдгүүдийг хэрхэн зөв тайлбарлахыг танд хэлсэн.

Аливаа квадрат, куб функцийн хувьд 4-р олон гишүүнт ба илүү өндөр зэрэгтэйМөн ташуу асимптотууд байдаггүй.

Одоо графикт ташуу асимптот байхгүй эсэхийг шалгацгаая. Тодорхой бус байдлыг илрүүлэхийн тулд бид ашигладаг Л'Хопиталын дүрэм:
, үүнийг шалгах шаардлагатай байсан.

Функц хязгааргүй өсөх үед түүний график ойртох шулуун шугам байхгүй хязгааргүй ойрхон.

Хичээлийн практик хэсэг рүү шилжье:

Функцийн графикийн асимптотуудыг хэрхэн олох вэ?

Үүнийг яг ингэж томъёолсон ердийн даалгавар, мөн энэ нь графикийн БҮХ асимптотуудыг (босоо, налуу/хэвтээ) олохыг хамарна. Хэдийгээр асуулт тавихдаа илүү нарийвчлалтай байхын тулд бид асимптот байгаа эсэхийг судлах талаар ярьж байна (эцсийн эцэст огт байхгүй байж магадгүй). Энгийн зүйлээс эхэлцгээе:

Жишээ 1

Функцийн графикийн асимптотуудыг ол

ШийдэлҮүнийг хоёр зүйлд хуваахад тохиромжтой:

1) Эхлээд бид босоо асимптот байгаа эсэхийг шалгана. -д хуваагч тэг болж, энэ үед функц хохирч байгаа нь шууд тодорхой болно төгсгөлгүй цоорхой, тэгшитгэлээр өгөгдсөн шулуун шугам нь функцийн графикийн босоо асимптот болно. Гэхдээ ийм дүгнэлт гаргахын өмнө нэг талын хязгаарлалтыг олох шаардлагатай.

Би өгүүлэлд яг адилхан анхаарч байсан тооцооллын техникийг танд сануулж байна Функцийн тасралтгүй байдал. Хагарлын цэгүүд. Хязгаарын тэмдгийн доорх илэрхийлэлд бид . Тоолуурт сонирхолтой зүйл алга:
.

Гэхдээ хуваагч дээр энэ нь гарч ирдэг хязгааргүй жижиг сөрөг тоо:
, энэ нь хязгаарын хувь заяаг тодорхойлдог.

Зүүн талын хязгаар нь хязгааргүй бөгөөд зарчмын хувьд босоо асимптот байгаа эсэх талаар дүгнэлт гаргах боломжтой болсон. Гэхдээ нэг талын хязгаарлалт нь зөвхөн үүнд шаардагдахгүй - тэд ойлгоход тусалдаг ХЭРХЭНфункцийн графикийг олоод түүнийг байгуул ЗӨВ. Тиймээс бид баруун гар талын хязгаарыг тооцоолох ёстой.

Дүгнэлт: нэг талт хязгаар нь хязгааргүй бөгөөд энэ нь шулуун шугам нь функцийн графикийн босоо асимптот гэсэн үг юм.

Эхний хязгаар хязгаарлагдмал, энэ нь "яриагаа үргэлжлүүлэх" шаардлагатай бөгөөд хоёр дахь хязгаарыг олох шаардлагатай гэсэн үг юм.

Хоёр дахь хязгаар нь бас хязгаарлагдмал.

Тиймээс бидний асимптот нь:

Дүгнэлт: тэгшитгэлээр өгөгдсөн шулуун шугам нь функцийн графикийн хэвтээ асимптот болно.

Хэвтээ асимптотыг олохын тулд
Та хялбаршуулсан томъёог ашиглаж болно:

Хэрэв байгаа бол хязгаарлагдмалхязгаар, тэгвэл шулуун шугам нь функцийн графикийн хэвтээ асимптот болно.

Функцийн тоологч ба хуваагч гэдгийг харахад хялбар байдаг өсөлтийн ижил дараалал, энэ нь хайж буй хязгаар нь хязгаарлагдмал байх болно гэсэн үг юм: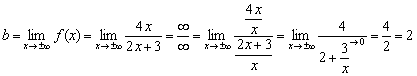

Хариулах:

Нөхцөлийн дагуу та зургийг дуусгах шаардлагагүй, гэхдээ бүрэн дүүрэн байгаа бол функциональ судалгаа, дараа нь бид ноорог дээр тэр даруй ноорог зурна.

Гурван олсон хязгаар дээр үндэслэн функцийн график хэрхэн байрлаж болохыг олж мэдэхийг хичээ. Ер нь хэцүү юу? 5-6-7-8 цэгүүдийг олоод зурган дээр тэмдэглэ. Гэхдээ энэ функцын графикийг ашиглан бүтээгдсэн энгийн функцийн графикийн хувиргалт, мөн дээрх нийтлэлийн 21-р жишээг анхааралтай судалж үзсэн уншигчид энэ нь ямар төрлийн муруй болохыг амархан таах боломжтой.

Жишээ 2

Функцийн графикийн асимптотуудыг ол

Энэ бол та өөрөө шийдэх жишээ юм. Процесс нь босоо асимптот ба ташуу асимптот гэсэн хоёр цэгт хуваагддаг гэдгийг танд сануулъя. Түүврийн шийдэлд хэвтээ асимптотыг хялбаршуулсан схемийг ашиглан олно.

Практикт бутархай-рационал функцүүд ихэвчлэн тулгардаг бөгөөд гиперболын талаар сургасны дараа бид даалгаврыг хүндрүүлнэ.

Жишээ 3

Функцийн графикийн асимптотуудыг ол

Шийдэл: Нэг, хоёр, дууссан:

1) Босоо асимптотууд байрладаг хязгааргүй тасалдалтай цэгүүдэд, тиймээс та хуваагч тэг болж байгаа эсэхийг шалгах хэрэгтэй. Шийдье квадрат тэгшитгэл:

Дискриминант эерэг тул тэгшитгэл нь хоёр бодит язгууртай бөгөөд ажил нь мэдэгдэхүйц нэмэгдсэн =)

Цаашид нэг талын хязгаарыг олохын тулд квадрат гурвалжинхүчин зүйлчлэл хийхэд тохиромжтой:
(авсаархан тэмдэглэгээний хувьд "хасах" хэсгийг эхний хаалтанд оруулсан болно). Аюулгүй байхын тулд үүнийг оюун ухаанаар эсвэл ноорог дээр хаалт нээх замаар шалгацгаая.

Функцийг хэлбэрээр дахин бичье

Нэг талт хязгаарыг олъё:

Тэгээд цэг дээр:

Тиймээс шулуун шугамууд нь тухайн функцийн графикийн босоо асимптотууд юм.

2) Хэрэв та функцийг харвал , тэгвэл хязгаар нь хязгаарлагдмал байх нь тодорхой бөгөөд бид хэвтээ асимптоттой болно. Түүний оршихуйг товчхон харуулъя:

Тиймээс шулуун шугам (абсцисса тэнхлэг) нь энэ функцийн графикийн хэвтээ асимптот юм.

Хариулах:

Олдсон хязгаар ба асимптотууд нь функцийн графикийн талаар маш их мэдээлэл өгдөг. Дараахь баримтуудыг харгалзан зургийг оюун ухаанаараа төсөөлөхийг хичээ.

Графикийн хувилбарыг ноорог дээрээ зур.

Мэдээжийн хэрэг, олсон хязгаарлалтууд нь графикийн харагдах байдлыг тодорхой тодорхойлдоггүй бөгөөд та алдаа гаргаж магадгүй ч дасгал нь өөрөө дасгал хийх явцад үнэлж баршгүй тусламж үзүүлэх болно. бүрэн функциональ судалгаа. Зөв зураг нь хичээлийн төгсгөлд байна.

Жишээ 4

Функцийн графикийн асимптотуудыг ол

Жишээ 5

Функцийн графикийн асимптотуудыг ол

Эдгээр нь бие даасан шийдэлд зориулагдсан ажлууд юм. График хоёулаа дахин хэвтээ асимптотуудтай бөгөөд тэдгээрийг дараах шинж чанаруудаар шууд илрүүлдэг: Жишээ 4-т өсөлтийн дараалалхуваагч илүү, тоологчийн өсөлтийн дарааллаас илүү, жишээ 5-д тоологч ба хуваагч өсөлтийн ижил дараалал. Түүврийн шийдэлд эхний функцийг ташуу асимптотууд байгаа эсэхийг бүрэн, хоёр дахь нь хязгаараар шалгана.

Миний субьектив сэтгэгдэлээр хэвтээ асимптотууд нь "үнэхээр хазайсан"-аас илт илүү түгээмэл байдаг. Удаан хүлээгдэж буй ерөнхий тохиолдол:

Жишээ 6

Функцийн графикийн асимптотуудыг ол

Шийдэл: жанрын сонгодог:

1) хуваагч эерэг байх тул функц тасралтгүйбүх тооны шугамын дагуу байх ба босоо асимптот байхгүй. ...Энэ сайн уу? Зөв үг биш - маш сайн! 1-р цэг хаалттай байна.

2) Ташуу асимптот байгаа эсэхийг шалгая:

Эхний хязгаар хязгаарлагдмал, тэгээд цаашаа явцгаая. Тооцооллын явцад хоёр дахь хязгаарыг арилгах тодорхойгүй байдал "хязгааргүйг хасах"Бид илэрхийллийг нийтлэг хуваагч руу авчирдаг: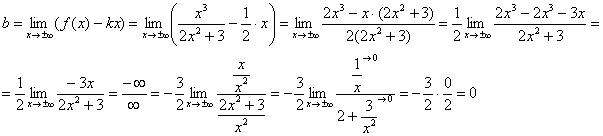

Хоёр дахь хязгаар нь бас хязгаарлагдмалТиймээс тухайн функцийн график нь ташуу асимптоттой байна:

Дүгнэлт:

Ийнхүү функцийн график үед хязгааргүй ойрхоншулуун шугам руу ойртоно:

Энэ нь ташуу асимптотыг гарал үүслээр нь огтолж байгааг анхаарна уу, ийм огтлолцлын цэгүүд нь нэлээд зөвшөөрөгдөхүйц байдаг - хязгааргүйд "бүх зүйл хэвийн" байх нь чухал (үнэндээ энд бид асимптотуудын тухай ярьж байна).

Жишээ 7

Функцийн графикийн асимптотуудыг ол

Шийдэл: Сэтгэгдэл бичих онцгой зүйл байхгүй тул би үүнийг албан ёсоор болгоё ойролцоогоор дээжэцсийн шийдэл:

1) Босоо асимптотууд. Гол санааг нь судалцгаая.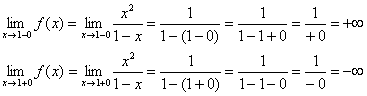

Шулуун шугам нь графын босоо асимптот юм.

2) Ташуу асимптотууд:

Шулуун шугам нь графын налуу асимптот юм.

Хариулах:

Олдсон нэг талын хязгаар ба асимптотууд нь энэ функцийн график ямар харагдахыг маш итгэлтэйгээр таамаглах боломжийг бидэнд олгодог. Хичээлийн төгсгөлд зөв зурах.

Жишээ 8

Функцийн графикийн асимптотуудыг ол

Энэ нь бие даасан шийдлийн жишээ юм, зарим хязгаарыг тооцоолоход хялбар байхын тулд та хуваагчийг нэр томъёогоор хувааж болно. Дахин хэлэхэд, үр дүндээ дүн шинжилгээ хийхдээ энэ функцийн графикийг зурж үзээрэй.

Мэдээжийн хэрэг, "жинхэнэ" ташуу асимптотуудын эзэд нь эдгээрийн графикууд юм. бутархай рационал функцууд, тоологчийн өндөр зэрэгтэй дахиад нэгхуваагчийн хамгийн дээд зэрэг. Хэрэв энэ нь илүү байвал ташуу асимптот байхгүй болно (жишээлбэл, ).

Гэхдээ амьдралд бусад гайхамшгууд тохиолддог:

Жишээ 9

Жишээ 11

Асимптот байгаа эсэхийг функцийн графикийг шалгана уу

Шийдэл: Энэ нь ойлгомжтой , тиймээс бид функцийн график байгаа баруун хагас хавтгайг л авч үзнэ.

Тиймээс шулуун шугам (ординатын тэнхлэг) нь функцийн графикийн босоо асимптот болно.

2) Ташуу асимптотын судалгааг бүрэн схемийн дагуу хийж болно, гэхдээ нийтлэлд L'Hopital-ийн дүрэмшугаман функц илүү байгааг бид олж мэдсэн өндөр захиалгаөсөлт логарифмээс илүү, тиймээс: (Ижил хичээлийн 1-р жишээг үзнэ үү).

Дүгнэлт: x тэнхлэг нь функцийн графикийн хэвтээ асимптот юм.

Хариулах:
, Хэрэв ;
, Хэрэв .

Тодорхой болгохын тулд зурах:

Ижил төстэй функц нь огт асимптотгүй байдаг нь сонирхолтой юм (хүссэн хүмүүс үүнийг шалгаж болно).

Сүүлийн хоёр жишээ бие даан суралцах:

Жишээ 12

Асимптот байгаа эсэхийг функцийн графикийг шалгана уу

Мөн танд бие даан шийдвэрлэх асуудлууд гарч ирэх бөгөөд үүний хариултыг та харж болно.

Асимптотын тухай ойлголт

Хэрэв та эхлээд муруйн асимптотуудыг байгуулбал ихэнх тохиолдолд функцийн графикийг бүтээх нь илүү хялбар болно.

Асимптотын хувь заяа эмгэнэлээр дүүрэн байдаг. Энэ нь юу болохыг төсөөлөөд үз дээ: бүх амьдрал тань нандин зорилгодоо чиглэн, түүндээ аль болох ойртсон боловч хэзээ ч хүрч чадахгүй. Жишээ нь, таны холболтыг хичээ амьдралын замхүссэн хүнийхээ замд, хэзээ нэгэн цагт түүнд бараг ойртох боловч түүнд хүрч болохгүй. Эсвэл тэрбум олохыг хичээ, гэхдээ энэ зорилгодоо хүрч, Гиннесийн амжилтын номонд орохоос өмнө хэдэн зуун цент дутуу байна. Гэх мэт. Энэ нь асимптоттой адил юм: энэ нь функцийн графикийн муруйд хүрэхийг байнга эрмэлздэг, хамгийн бага боломжит зайд ойртдог боловч хэзээ ч хүрдэггүй.

Тодорхойлолт 1. Хувьсагч нь хязгааргүй нэмэх эсвэл хасах хязгаартай байх үед функцийн график дур мэдэн ойртож буй шулуун шугамуудыг асимптот гэнэ.

Тодорхойлолт 2. Хувьсах цэгээс хол зайтай бол шулуун шугамыг функцийн графикийн асимптот гэнэ. МЭнэ шугам хүртэлх функцийн график нь цэг тодорхойгүй хугацаагаар холдох тусам тэг болох хандлагатай байна Мфункцийн графикийн аль нэг салааны дагуух эх үүсвэрээс.

Босоо, хэвтээ, ташуу гэсэн гурван төрлийн асимптот байдаг.

Босоо асимптотууд

Босоо асимптотуудын талаар хамгийн түрүүнд мэдэх ёстой зүйл бол тэдгээр нь тэнхлэгтэй параллель байх явдал юм Өө .

Тодорхойлолт. Шулуун x = абайна функцийн графикийн босоо асимптот , хэрэв цэг x = абайна хоёр дахь төрлийн тасалдалын цэгЭнэ функцийн хувьд.

Тодорхойлолтоос харахад шулуун шугам x = ань функцийн графикийн босоо асимптот юм е(x) дор хаяж нэг нөхцөл хангагдсан бол:

Энэ тохиолдолд функц е(x) ямар ч үед тус тус тодорхойлогдоогүй байж болно x ≥ аТэгээд x ≤ а .

Сэтгэгдэл:

Жишээ 1.Функцийн график y=ln xбосоо асимптоттой x= 0 (өөрөөр хэлбэл тэнхлэгтэй давхцаж байна Өө) тодорхойлолтын домэйны хил дээр, учир нь функцийн хязгаар нь баруун талаас тэг рүү чиглэдэг х нь хязгааргүйтэй тэнцүү байна:

(дээрх зураг).

өөрөө, дараа нь шийдлүүдийг хар

Жишээ 2.Функцийн графикийн асимптотуудыг ол.

Жишээ 3.Функцийн графикийн асимптотуудыг ол

Хэвтээ асимптотууд

Хэвтээ асимптотуудын талаар мэдэх ёстой хамгийн эхний зүйл бол тэдгээр нь тэнхлэгтэй параллель байх явдал юм Үхэр .

Хэрэв (аргумент нэмэх эсвэл хасах хязгааргүй байх хандлагатай функцын хязгаар нь тодорхой утгатай тэнцүү бол) б), Тэр y = б – хэвтээ асимптот муруй y = е(x ) (X нэмэх хязгааргүй байх хандлагатай үед баруун талд, X хасах хязгааргүй байх хандлагатай үед зүүн талд, хэрэв X нэмэх эсвэл хасах хязгааргүй байх хандлагатай бол хоёр талт).

Жишээ 5.Функцийн график

цагт а> 1 нь хэвтээ ассимпототыг орхисон y= 0 (өөрөөр хэлбэл тэнхлэгтэй давхцаж байна Үхэр), "x" гэсэн функцийн хязгаар нь хасах хязгааргүй байх хандлагатай тул тэг болно:

"x" гэсэн функцийн хязгаар нь хязгааргүй нэмэх хандлагатай байдаг тул муруй нь зөв хэвтээ асимптотгүй:

Ташуу асимптотууд

Бидний дээр судалсан босоо болон хэвтээ асимптотууд нь координатын тэнхлэгүүдтэй параллель байдаг тул тэдгээрийг бүтээхэд зөвхөн тодорхой тоо буюу асимптот дамждаг абсцисса эсвэл ординатын тэнхлэг дээрх цэг хэрэгтэй болно. Ташуу асимптотын хувьд илүү том налуу хэрэгтэй к, энэ нь шугамын налуу өнцөг, чөлөөт нэр томъёог харуулж байна б, энэ нь шугам нь эхээс хэр их эсвэл доор байгааг харуулдаг. Аналитик геометр, түүнээс шулуун шугамын тэгшитгэлийг мартаагүй хүмүүс ташуу асимптотын хувьд олж болохыг анзаарах болно. налуутай шулууны тэгшитгэл. Ташуу асимптот байгаа эсэхийг дараах теоремоор тодорхойлж, үүний үндсэн дээр сая дурдсан коэффициентүүдийг олно.

Теорем.Муруй болгохын тулд y = е(x) асимптоттой байсан y = kx + б , хязгаарлагдмал хязгаар байх нь зайлшгүй бөгөөд хангалттай юм кТэгээд бхувьсагч хандлагаар авч үзэж буй функцийн xнэмэх хязгаар, хасах хязгаар:

(1)

(2)

Ийм байдлаар олдсон тоонууд кТэгээд бба ташуу асимптот коэффициентууд.

Эхний тохиолдолд (х нь хязгааргүй нэмэх хандлагатай байдаг тул) баруун налуу асимптот, хоёр дахь тохиолдолд (х хасах хязгааргүй байх хандлагатай байдаг тул) зүүн ташуу асимптотыг олж авна. Баруун ташуу асимптотыг Зураг дээр үзүүлэв. доор.

Ташуу асимптотын тэгшитгэлийг олохдоо X-ийн нэмэх хязгааргүй ба хасах хязгааргүй байдлын аль алинд нь хандах хандлагыг харгалзан үзэх шаардлагатай. Зарим функцүүдийн хувьд, жишээлбэл, бутархай оновчтой функцүүдийн хувьд эдгээр хязгаарууд давхцдаг боловч олон функцүүдийн хувьд эдгээр хязгаарууд өөр бөгөөд тэдгээрийн зөвхөн нэг нь байж болно.

Хэрэв хязгаарууд давхцаж, x нь хязгааргүй, хасах хязгааргүй байх хандлагатай байвал шулуун шугам y = kx + б нь муруйн хоёр талт асимптот юм.

Хэрэв асимптотыг тодорхойлох хязгаарын нэгээс доошгүй бол y = kx + б , байхгүй бол функцийн графикт ташуу асимптот байхгүй (гэхдээ босоо байрлалтай байж болно).

Хэвтээ асимптот байгааг харахад хялбар байдаг y = бташуу онцгой тохиолдол юм y = kx + бцагт к = 0 .

Тиймээс хэрэв аль нэг чиглэлд муруй нь хэвтээ асимптоттой бол энэ чиглэлд налуу байхгүй ба эсрэгээр.

Жишээ 6.Функцийн графикийн асимптотуудыг ол

Шийдэл. Функц нь бүхэл тоон мөрөнд тодорхойлогддог x= 0, өөрөөр хэлбэл.

Тиймээс, эвдрэх цэг дээр x= 0 муруй нь босоо асимптоттой байж болно. Үнэн хэрэгтээ, x нь зүүнээс тэг рүү чиглэж байгаа функцийн хязгаар нь нэмэх хязгаартай тэнцүү байна:

Тиймээс, x= 0 – энэ функцийн графикийн босоо асимптот.

Энэ функцийн график нь хэвтээ асимптотгүй, учир нь функцийн хязгаар нь нэмэх хязгаарыг нэмэх хандлагатай байдаг тул:

Ташуу асимптот байгаа эсэхийг олж мэдье.

Хязгаарлагдмал хязгаартай к= 2 ба б= 0. Шулуун y = 2xнь энэ функцийн графикийн хоёр талын налуу асимптот юм (жишээний доторх зураг).

Жишээ 7.Функцийн графикийн асимптотуудыг ол

Шийдэл. Функц нь нэг таслах цэгтэй x= −1. Нэг талын хязгаарыг тооцоолж, тасалдалын төрлийг тодорхойлъё.

Дүгнэлт: x= −1 нь хоёр дахь төрлийн тасалдлын цэг тул шулуун шугам x= −1 нь энэ функцийн графикийн босоо асимптот юм.

Бид ташуу асимптотуудыг хайж байна. Энэ функц нь бутархай-рациональ учраас at болон at хязгаарууд давхцдаг. Тиймээс бид тэгшитгэлд шулуун шугам - ташуу асимптотыг орлуулах коэффициентийг олно.

Олдсон коэффициентүүдийг налуугийн коэффициент бүхий шулуун шугамын тэгшитгэлд орлуулснаар ташуу асимптотын тэгшитгэлийг олж авна.

y = −3x + 5 .

Зураг дээр функцийн графикийг burgundy өнгөөр, асимптотуудыг хараар зааж өгсөн болно.

Жишээ 8.Функцийн графикийн асимптотуудыг ол

Шийдэл. Энэ функц тасралтгүй байдаг тул түүний график нь босоо асимптотгүй. Бид ташуу асимптотуудыг хайж байна:

Тиймээс энэ функцийн график нь асимптоттой байна y= 0 үед ба асиптот байхгүй байна.

Жишээ 9.Функцийн графикийн асимптотуудыг ол

Шийдэл. Эхлээд бид босоо асимптотуудыг хайдаг. Үүнийг хийхийн тулд функцийн тодорхойлолтын мужийг олно. Функц нь тэгш бус байх үед тодорхойлогдоно. Хувьсагчийн тэмдэг xтэмдэгтэй таарч байна. Тиймээс эквивалент тэгш бус байдлыг авч үзье. Үүнээс бид функцийн тодорхойлолтын мужийг олж авна. . Босоо асимптот нь зөвхөн функцийн тодорхойлолтын домэйны хил дээр байж болно. Гэхдээ x= 0 нь босоо асимптот байж болохгүй, учир нь функц нь дээр тодорхойлогддог x = 0 .

Баруун гар талын хязгаарыг (зүүн гар талын хязгаарлалт байхгүй) авч үзье.

Цэг x= 2 нь хоёр дахь төрлийн тасархай цэг тул шулуун шугам x= 2 - энэ функцийн графикийн босоо асимптот.

Бид ташуу асимптотуудыг хайж байна:

Тэгэхээр, y = x+ 1 - энэ функцийн графикийн ташуу асимптот. Бид ташуу асимптотыг хайж байна:

Тэгэхээр, y = −x − 1 - үед ташуу асимптот .

Жишээ 10.Функцийн графикийн асимптотуудыг ол

Шийдэл. Функц нь тодорхойлолтын мужтай байдаг . Энэ функцийн графикийн босоо асимптот нь зөвхөн тодорхойлолтын мужын хил дээр байж болох тул функцийн нэг талт хязгаарыг -ээс олно.

Функцийн графикийн асимптот y = f(x) нь графикийн цэг эх цэгээс тодорхойгүй хугацаагаар шилжих үед (x, f(x)) цэгээс энэ шулуун хүртэлх зай тэг рүү чиглэх шинж чанартай шулуун шугам юм.

Зураг 3.10-д. график жишээг үзүүлэв босоо, хэвтээТэгээд налууасимптот.

Графикийн асимптотуудыг олох нь дараах гурван теорем дээр суурилдаг.

Босоо асимптотын теорем. y = f(x) функцийг x 0 цэгийн зарим хөршид (энэ цэгийг оруулаагүй байж магадгүй) тодорхойлогдох ба функцийн нэг талт хязгаарын ядаж нэг нь хязгааргүйтэй тэнцүү байна, өөрөөр хэлбэл. Тэгвэл x = x 0 шулуун нь y = f(x) функцийн графикийн босоо асимптот болно.

Хэрэв функц x 0 цэг дээр тасралтгүй байвал x = x 0 шулуун шугам нь босоо асимптот болж чадахгүй нь ойлгомжтой, учир нь энэ тохиолдолд . Иймээс босоо асимптотуудыг функцийн тасалдал эсвэл түүний тодорхойлолтын хүрээний төгсгөлд хайх хэрэгтэй.

Хэвтээ асимптотын теорем. Хангалттай том х-ийн хувьд y = f(x) функцийг тодорхойлъё, функцийн хязгаарлагдмал хязгаар байна. Тэгвэл y = b шугам нь функцийн графикийн хэвтээ асимптот болно.

Сэтгэгдэл. Хэрэв хязгааруудын зөвхөн нэг нь хязгаарлагдмал бол функц нь зохих ёсоор: зүүн гартайэсвэл баруун талтайхэвтээ асимптот.

Энэ тохиолдолд функц нь ташуу асимптоттой байж болно.

Ташуу асимптотын теорем. Хангалттай том х-ийн хувьд y = f(x) функцийг тодорхойлж, хязгаарлагдмал хязгаартай байг . Дараа нь y = kx + b шулуун шугам нь функцийн графикийн налуу асимптот болно.

Нотлох баримт байхгүй.

Хэрэв харгалзах хязгаарын суурь нь тодорхой тэмдгийн хязгааргүй байдлыг агуулж байвал ташуу асимптот нь хэвтээ шиг баруун гар эсвэл зүүн гартай байж болно.

Функцуудыг судлах, тэдгээрийн графикийг бүтээх нь ихэвчлэн дараах алхмуудыг агуулна.

1. Функцийн тодорхойлолтын мужийг ол.

2. Функцийг тэгш сондгой байгаа эсэхийг шалга.

3. Хэрэв хязгаарлагдмал бол тасархайн цэгүүд болон тодорхойлолтын мужын хил дэх функцийн зан төлөвийг судалж босоо асимптотуудыг ол.

4. Хязгааргүй үед функцийн зан төлөвийг судалж хэвтээ эсвэл ташуу асимптотуудыг ол.

5. Функцийн монотон байдлын экстремум ба интервалыг ол.

6. Функцийн гүдгэр ба гулзайлтын цэгийн интервалыг ол.

7. Координатын тэнхлэгүүдтэй огтлолцох цэгүүд болон магадгүй графикийг тодруулах нэмэлт цэгүүдийг ол.

Функцийн дифференциал

Хэрэв функц нь тодорхой суурийн хувьд хязгаарлагдмал тоотой тэнцүү хязгаартай бол түүнийг энэ тооны нийлбэр ба ижил суурийн хувьд хязгааргүй бага утгатай (болон эсрэгээр) илэрхийлж болно гэдгийг баталж болно: .

Энэ теоремыг дифференциалагдах функцэд хэрэглэе: .

Тиймээс Dу функцийн өсөлт нь хоёр гишүүнээс бүрдэнэ: 1) Dx-тэй харьцуулахад шугаман, i.e. f `(x)Dх; 2) Dx-ийн хувьд шугаман бус, i.e. a(Dx)Dх. Үүний зэрэгцээ, тэр цагаас хойш , энэ хоёр дахь гишүүн нь Dx-ээс өндөр эрэмбийн хязгааргүй жижиг тоо юм (Dx тэг рүү тэмүүлдэг тул илүү хурдан тэглэх хандлагатай байдаг).

Дифференциалфункцийн өсөлтийн Dx-тэй харьцуулахад үндсэн, шугаман хэсэг гэж нэрлэгддэг, бүтээгдэхүүнтэй тэнцүү байна dy = f `(x)Dх бие даасан хувьсагчийн өсөлтийн дериватив.

y = x функцийн дифференциалыг олъё.

dy = f `(x)Dх = x`Dх = Dх тул dx = Dх, i.e. бие даасан хувьсагчийн дифференциал нь энэ хувьсагчийн өсөлттэй тэнцүү байна.

Иймд функцийн дифференциалын томьёог dy = f `(x)dх гэж бичиж болно. Ийм учраас деривативын тэмдэглэгээний нэг нь dy/dx бутархай юм.

Геометрийн утгадифференциал дүрсэлсэн
Зураг 3.11. y = f(x) функцийн график дээр дурын M(x, y) цэгийг авъя. Аргумент x-д Dx өсөлтийг өгье. Дараа нь y = f(x) функц нь Dy = f(x + Dх) - f(x) өсөлтийг хүлээн авна. Абсцисса тэнхлэгийн эерэг чиглэлтэй а өнцгийг үүсгэдэг M цэг дээрх функцийн график руу шүргэгч зуръя, өөрөөр хэлбэл. f `(x) = бор а. -аас зөв гурвалжин MKN
KN = MN*tg a = Dх*tg a = f `(x)Dх = dy.

Ийнхүү функцийн дифференциал нь x нь Dx өсөлтийг хүлээн авах үед тухайн цэг дэх функцийн графикт татсан шүргэгчийн ординатын өсөлт юм.

Дифференциалын шинж чанарууд нь деривативын шинж чанаруудтай үндсэндээ ижил байна:

3. d(u ± v) = du ± dv.

4. d(uv) = v du + u dv.

5. d(u/v) = (v du - u dv)/v 2.

Гэсэн хэдий ч функцийн дифференциалын деривативт байдаггүй чухал шинж чанар байдаг - энэ нь тийм юм дифференциал хэлбэрийн инвариант байдал.

y = f(x) функцийн дифференциалын тодорхойлолтоос dy = f `(x)dх дифференциал. Хэрэв энэ функц y нь нарийн төвөгтэй бол i.e. y = f(u), энд u = j(x), дараа нь y = f ба f `(x) = f `(u)*u` болно. Дараа нь dy = f `(u)*u`dх. Гэхдээ функцийн хувьд
u = j(x) дифференциал du = u`dх. Эндээс dy = f `(u)*du.

dy = f `(x)dх ба dy = f `(u)*du тэгшитгэлүүдийг харьцуулж үзвэл бид x бие даасан хувьсагчийн функцийн оронд функцийг авч үзвэл дифференциал томъёо өөрчлөгдөхгүй эсэхийг шалгана. хамааралтай хувьсагч u. Дифференциалын энэ шинж чанарыг дифференциал хэлбэрийн (эсвэл томьёоны) инвариант байдал (өөрөөр хэлбэл өөрчлөгддөггүй) гэж нэрлэдэг.

Гэсэн хэдий ч эдгээр хоёр томъёонд ялгаа байсаар байна: тэдгээрийн эхнийх нь бие даасан хувьсагчийн дифференциал нь энэ хувьсагчийн өсөлттэй тэнцүү байна, өөрөөр хэлбэл. dx = Dx, хоёрдугаарт, du функцийн дифференциал нь энэ Du функцийн өсөлтийн зөвхөн шугаман хэсэг бөгөөд зөвхөн жижиг Dх du » Du.

Шийдлийг хоёр цэгт хялбархан хувааж болно:

1) Эхлээд бид босоо асимптот байгаа эсэхийг шалгана. Хуваагч нь тэг рүү очих бөгөөд энэ үед функц хязгааргүй тасалдлыг амсах бөгөөд тэгшитгэлээр тодорхойлсон шулуун шугам нь функцийн графикийн босоо асимптот болох нь шууд тодорхой болно. Гэхдээ ийм дүгнэлт гаргахын өмнө нэг талын хязгаарлалтыг олох шаардлагатай.

"Функцийн тасралтгүй байдал" гэсэн өгүүлэлд мөн адил онцолсон тооцооллын техникийг би танд сануулж байна. Хагарлын цэгүүд. Хязгаарын тэмдгийн доорх илэрхийлэлд "X"-ийг орлуулна. Тоолуурт сонирхолтой зүйл алга:

Гэхдээ хуваагч нь хязгааргүй бага сөрөг тоог үүсгэдэг:

Энэ нь хязгаарын хувь заяаг тодорхойлдог.

Зүүн талын хязгаар нь хязгааргүй бөгөөд зарчмын хувьд босоо асимптот байгаа эсэх талаар дүгнэлт гаргах боломжтой болсон. Гэхдээ нэг талт хязгаарлалтууд нь зөвхөн үүнд шаардлагатай биш бөгөөд тэдгээр нь функцийн график хэрхэн байрлаж байгааг ОЙЛГОХ, ЗӨВ бүтээхэд туслана. Тиймээс бид баруун гар талын хязгаарыг тооцоолох ёстой.

Дүгнэлт: нэг талт хязгаар нь хязгааргүй бөгөөд энэ нь шулуун шугам нь at функцийн графикийн босоо асимптот гэсэн үг юм.

Эхний хязгаар нь хязгаарлагдмал бөгөөд энэ нь бид "яриагаа үргэлжлүүлж" хоёр дахь хязгаарыг олох хэрэгтэй гэсэн үг юм.

Хоёр дахь хязгаар нь бас хязгаартай.

Тиймээс бидний асимптот нь:

Дүгнэлт: тэгшитгэлээр тодорхойлсон шулуун шугам нь функцийн графикийн хэвтээ асимптот юм.

Хэвтээ асимптотыг олохын тулд та хялбаршуулсан томъёог ашиглаж болно.

Хэрэв хязгаарлагдмал хязгаар байгаа бол шулуун шугам нь at функцийн графикийн хэвтээ асимптот болно.

Функцийн тоологч ба хуваагч нь ижил өсөлтийн дарааллаар байгааг анзаарахад хялбар байдаг бөгөөд энэ нь хайж буй хязгаар нь төгсгөлтэй байна гэсэн үг юм.

Нөхцөлийн дагуу зураг зурах шаардлагагүй, гэхдээ хэрэв бид функцийг судалж байгаа бол тэр даруй ноорог дээр ноорог зурна.

Олдсон гурван хязгаар дээр үндэслэн функцийн график хэрхэн байрлаж болохыг өөрөө олж мэдээрэй. Ер нь хэцүү юу? 5-6-7-8 цэгүүдийг олоод зурган дээр тэмдэглэ. Гэхдээ энэ функцийн графикийг график хувиргалтыг ашиглан бүтээдэг үндсэн функц, мөн дээрх нийтлэлийн 21-р жишээг анхааралтай судалж үзсэн уншигчид энэ нь ямар төрлийн муруй болохыг амархан таах боломжтой.

Функцийн графикийн асимптотуудыг ол

Шийдэл: Нэг, хоёр, дууссан:

1) Босоо асимптотууд нь хязгааргүй тасархай цэгүүд дээр байдаг тул хуваагч тэг болж байгаа эсэхийг шалгах хэрэгтэй. Шийдье квадрат тэгшитгэл:

Ялгаварлан гадуурхагч нь эерэг тул тэгшитгэл нь хоёр бодит үндэстэй бөгөөд ажил нь мэдэгдэхүйц нэмэгддэг

Цаашид нэг талт хязгаарыг олохын тулд дөрвөлжин гурвалсан тоог үржүүлэх нь тохиромжтой.

(авсаархан тэмдэглэгээний хувьд "хасах" хэсгийг эхний хаалтанд оруулсан болно). Аюулгүй байхын тулд үүнийг оюун ухаанаар эсвэл ноорог дээр хаалт нээх замаар шалгацгаая.

Функцийг хэлбэрээр дахин бичье

Нэг талт хязгаарыг олъё:

асимптот график функцийн хязгаар

Тэгээд цэг дээр:

Тиймээс шулуун шугамууд нь тухайн функцийн графикийн босоо асимптотууд юм.

2) Хэрэв та функцийг харвал хязгаар нь хязгаарлагдмал байх нь тодорхой бөгөөд бид хэвтээ асимптоттой болно. Түүний оршихуйг товчхон харуулъя:

Тиймээс шулуун шугам (абсцисса тэнхлэг) нь энэ функцийн графикийн хэвтээ асимптот юм.

Графикийн хувилбарыг ноорог дээрээ зур.

Мэдээжийн хэрэг, олсон хязгаарлалтууд нь графикийн харагдах байдлыг тодорхой тодорхойлдоггүй бөгөөд та алдаа гаргаж магадгүй ч дасгал нь өөрөө дасгал хийх явцад үнэлж баршгүй тусламж үзүүлэх болно. бүрэн судалгаафункцууд. Зөв зураг нь хичээлийн төгсгөлд байна.

Функцийн графикийн асимптотуудыг ол

Эдгээр нь бие даасан шийдэлд зориулагдсан ажлууд юм. Хоёр график дахин хэвтээ асимптотуудтай бөгөөд эдгээрийг дараах шинж тэмдгүүдээр шууд илрүүлдэг: Жишээ 4-т хуваагчийн өсөлтийн дараалал нь хүртэгчийн өсөлтийн дарааллаас их, жишээ 5-д тоологч ба хуваагч нь өсөлтийн ижил дараалал. Түүврийн шийдэлд эхний функцийг ташуу асимптотуудыг бүрэн хэмжээгээр, хоёрдугаарт - хязгаараар шалгана.

Функцийн графикийн асимптотуудыг ол

Шийдэл: жанрын сонгодог:

1) Хуваагч эерэг тул функц нь бүх тооны шугамын дагуу тасралтгүй байх ба босоо асимптот байхгүй. ...Энэ сайн уу? Зөв үг биш - маш сайн! 1-р цэг хаалттай байна.
2) Ташуу асимптот байгаа эсэхийг шалгая:

Хоёрдахь хязгаар нь мөн төгсгөлтэй тул тухайн функцийн график нь ташуу асимптоттой байна:

Ийнхүү функцийн график хязгааргүй ойрхон шулуун шугамд ойртох үед.

Функцийн графикийн асимптотуудыг ол

Шийдэл: тайлбар хийх онцгой зүйл байхгүй тул би эцсийн шийдлийн ойролцоо жишээг гаргая:

1) Босоо асимптотууд. Гол санааг нь судалцгаая.

Шулуун шугам нь графын босоо асимптот юм.

2) Ташуу асимптотууд:

Шулуун шугам нь графын налуу асимптот юм.

Олдсон нэг талын хязгаар ба асимптотууд нь энэ функцийн график ямар харагдахыг маш итгэлтэйгээр таамаглах боломжийг бидэнд олгодог.

Функцийн графикийн асимптотуудыг ол

Мэдээжийн хэрэг, "бодит" ташуу асимптотуудын эзэд нь тоологчийн хамгийн дээд зэрэг нь хуваагчийн хамгийн дээд зэргээс нэг их байх бутархай рационал функцүүдийн графикууд юм. Хэрэв энэ нь илүү байвал ташуу асимптот байхгүй болно (жишээлбэл).

Гэхдээ амьдралд бусад гайхамшгууд тохиолддог.

Гэр

Энэ нь тэдгээрийн тэгшитгэлийг олох, хэрэв асуудал шаардлагатай бол шулуун шугам зурах гэсэн үг юм. Үйл явц нь функцийн хязгаарыг олох явдал юм.

Функцийн графикийн асимптотууд

Тэгэхээр асимптот гэж юу вэ?

Функцийн график хэдэн асимптоттой байж болох вэ?

Энэ нь юу гэсэн үг вэ?

Функцийн графикийн босоо асимптотууд

Функцийн графикийн налуу асимптотууд

Функцийн графикийн асимптотуудыг хэрхэн олох вэ?

Хэвтээ асимптотыг олохын тулдТа хялбаршуулсан томъёог ашиглаж болно:

Асимптотын тухай ойлголт

Босоо асимптотууд

өөрөө, дараа нь шийдлүүдийг хар

Хэвтээ асимптотууд

Ташуу асимптотууд

Хэвтээ асимптотыг олохын тулд
Та хялбаршуулсан томъёог ашиглаж болно: