Сайн байна уу! Магадлалын тархалт гэж юу болохыг бид аль хэдийн мэддэг болсон. Энэ нь салангид эсвэл тасралтгүй байж болох бөгөөд бид үүнийг магадлалын нягтын функц гэж нэрлэдэг болохыг олж мэдсэн. магадлал. Учир нь тэнд би энэ бүгдийг илүү нарийвчлан авч үзэх болно. Энэ нь бид яг 2 толгой авах магадлал байх болно. Одоо хэд хэдэн нийтлэг хуваарилалтыг авч үзье., учир нь бид тэдгээрийг тэнцүү гэж үздэг.
Энд бид ямар шидэхэд толгой гарахыг сонирхохгүй байна. 5*4*3... Үүнийг 5!/2! гэж дахин бичиж болно.санамсаргүй хэмжигдэхүүнийг илэрхийлэх математик илэрхийлэл юм. Дискрет санамсаргүй хэмжигдэхүүнүүдийн хувьд энэхүү математик илэрхийллийг тархалтын функц гэж нэрлэдэг.
Хэрэв асуудал нь санамсаргүй хэмжигдэхүүнийг илэрхийлэх математикийн илэрхийлэлийг тодорхой бичих боломжийг олгодог бол та түүний аль нэг утгын яг магадлалыг тооцоолж болно. Энэ тохиолдолд та хуваарилалтын функцийн бүх утгыг тооцоолж, жагсааж болно. Санамсаргүй хэмжигдэхүүний янз бүрийн хуваарилалт бизнес, социологи, анагаах ухааны хэрэглээнд тулгардаг. Хамгийн ашигтай тархалтын нэг бол бином юм.
Бином тархалтдараах шинж чанаруудаар тодорхойлогддог нөхцөл байдлыг дуурайхад ашигладаг.
- Дээж нь тогтмол тооны элементүүдээс бүрдэнэ n, тодорхой туршилтын үр дүнг төлөөлдөг.
- Түүврийн элемент бүр нь түүврийн орон зайг бүхэлд нь шавхдаг бие биенээ үгүйсгэдэг хоёр ангиллын аль нэгэнд хамаарна. Ерөнхийдөө эдгээр хоёр ангиллыг амжилт, бүтэлгүйтэл гэж нэрлэдэг.
- Амжилтанд хүрэх магадлал rтогтмол байна. Тиймээс бүтэлгүйтэх магадлал өндөр байна 1 – х.
- Аливаа туршилтын үр дүн (жишээлбэл, амжилт эсвэл бүтэлгүйтэл) нь өөр туршилтын үр дүнгээс хамаардаггүй. Үр дүнгийн бие даасан байдлыг хангахын тулд дээжийн элементүүдийг ихэвчлэн хоёр өөр аргыг ашиглан авдаг. Түүврийн элемент бүрийг санамсаргүй байдлаар буцаахгүйгээр хязгааргүй олонлогоос эсвэл урвуу өөрчлөлттэй хязгаарлагдмал популяциас санамсаргүй байдлаар гаргаж авдаг.
Тэмдэглэлийг эсвэл форматаар, жишээнүүдийг форматаар татаж аваарай
-аас бүрдсэн түүврийн амжилтын тоог тооцоолоход бином тархалтыг ашигладаг nажиглалт. Захиалгыг жишээ болгон авч үзье. Захиалга өгөхийн тулд Саксон компанийн үйлчлүүлэгчид интерактив цахим маягтыг ашиглаж, компани руу илгээх боломжтой. Дараа нь мэдээллийн систем нь захиалгад алдаа, дутуу, буруу мэдээлэл байгаа эсэхийг шалгадаг. Асуудалтай бүх захиалгыг дарцаглаж, өдөр тутмын онцгой байдлын тайланд оруулсан болно. Компанийн цуглуулсан мэдээллээс харахад захиалгад алдаа гарах магадлал 0.1 байна. Тухайн түүвэрт тодорхой тооны алдаатай захиалга олох магадлал ямар байдгийг компани мэдэхийг хүсч байна. Жишээлбэл, үйлчлүүлэгчид дөрвийг дуусгалаа гэж бодъё цахим хэлбэрүүд. Бүх захиалга алдаагүй байх магадлал хэд вэ? Энэ магадлалыг хэрхэн тооцох вэ? Амжилттай бол бид маягтыг бөглөхдөө алдаа гарсныг ойлгох бөгөөд бусад бүх үр дүнг бүтэлгүйтсэн гэж үзнэ. Бид өгөгдсөн дээж дэх алдаатай захиалгын тоог сонирхож байгааг санаарай.
Бид ямар үр дүнг ажиглаж болох вэ? Хэрэв түүвэр дөрвөн дарааллаас бүрдсэн бол нэг, хоёр, гурав, дөрөв нь буруу, бүгд зөв байж болно. Буруу бөглөсөн маягтын тоог тодорхойлсон санамсаргүй хэмжигдэхүүн өөр ямар ч утгыг авч чадах уу? Буруу маягтын тоо нь түүврийн хэмжээнээс хэтэрч болохгүй тул энэ боломжгүй nэсвэл сөрөг байх. Тиймээс, бином тархалтын хуулийг дагаж мөрддөг санамсаргүй хэмжигдэхүүн нь 0-ээс утгыг авна n.
Дөрвөн захиалгын түүвэрт дараах үр дүн ажиглагдаж байна гэж үзье.
Заасан дарааллаар дөрвөн захиалгын түүврээс гурван алдаатай тушаал олох магадлал хэд вэ? Урьдчилсан судалгаагаар маягтыг бөглөхдөө алдаа гарах магадлал 0.10 байгаа тул дээрх үр дүнгийн магадлалыг дараах байдлаар тооцно.
Үр дүн нь бие биенээсээ хамаардаггүй тул үр дүнгийн заасан дарааллын магадлал нь тэнцүү байна: p*p*(1–p)*p = 0.1*0.1*0.9*0.1 = 0.0009. Хэрэв та сонголтын тоог тооцоолох шаардлагатай бол X nэлементүүдийн хувьд та хослолын томъёог (1) ашиглах хэрэгтэй:

хаана n! = n * (n –1) * (n – 2) * … * 2 * 1 - тооны факториал n, мөн 0! = 1 ба 1! Тодорхойлолтоор = 1.
Энэ илэрхийллийг ихэвчлэн гэж нэрлэдэг. Тиймээс хэрэв n = 4 ба X = 3 бол түүврийн хэмжээ 4-өөс гаргаж авсан гурван элементээс бүрдэх дарааллын тоог дараах томъёогоор тодорхойлно.
Тиймээс гурван алдаатай захиалгыг илрүүлэх магадлалыг дараах байдлаар тооцоолно.
(Боломжтой дарааллын тоо) *
(тодорхой дарааллын магадлал) = 4 * 0.0009 = 0.0036
Үүний нэгэн адил та дөрвөн захиалгын дунд нэг эсвэл хоёр алдаатай байх магадлалыг, мөн бүх захиалга алдаатай эсвэл бүгд зөв байх магадлалыг тооцоолж болно. Гэсэн хэдий ч түүврийн хэмжээ ихсэх тусам nтодорхой дарааллын үр дүнгийн магадлалыг тодорхойлох нь илүү хэцүү болно. Энэ тохиолдолд та сонголтын тооны бином тархалтыг тодорхойлсон тохирох математик загварыг ашиглах хэрэгтэй. Xагуулсан сонголтоос объектууд nэлементүүд.
Бином тархалт

Хаана P(X)- магадлал Xөгөгдсөн түүврийн хэмжээний амжилт nболон амжилтанд хүрэх магадлал r, X = 0, 1, … n.
Томъёо (2) нь зөн совингийн дүгнэлтийн албан ёсны хэлбэр гэдгийг анхаарна уу. Санамсаргүй хувьсагч X, хоёр нэрийн тархалтыг дагадаг 0-ээс бүхэл тоон утгыг авч болно n. Ажил rX(1 – х)n – X-аас бүрдэх тодорхой дарааллын магадлалыг илэрхийлнэ Xтүүврийн хэмжээтэй тэнцэх амжилт n. утга нь бүрдсэн боломжит хослолын тоог тодорхойлдог Xамжилт nтуршилтууд. Тиймээс өгөгдсөн тооны туршилтын хувьд nболон амжилтанд хүрэх магадлал r-аас бүрдэх дарааллын магадлал Xамжилт, тэнцүү
P(X) = (боломжтой дарааллын тоо) * (тодорхой дарааллын магадлал) = 
Томъёо (2)-ын хэрэглээг харуулсан жишээнүүдийг авч үзье.
1. Маягтыг буруу бөглөх магадлалыг 0.1 гэж үзье. Дөрвөн бөглөсөн маягтаас гурав нь буруу байх магадлал хэд вэ? Томъёо (2) ашиглан бид дөрвөн захиалгаас бүрдсэн түүвэрт гурван алдаатай захиалгыг илрүүлэх магадлал тэнцүү болохыг олж мэдэв.
2. Маягтыг буруу бөглөх магадлалыг 0.1 гэж үзье. Дөрвөн бөглөсөн маягтаас гурваас доошгүй нь буруу байх магадлал хэд вэ? Өмнөх жишээнд үзүүлсэнчлэн бөглөсөн дөрвөн маягтаас гурав нь буруу байх магадлал 0.0036 байна. Дөрвөн бөглөсөн маягтын дотроос гурваас доошгүй нь буруу байх магадлалыг тооцоолохын тулд бөглөсөн дөрвөн маягтаас гурав нь буруу байх магадлалыг, дөрвөн бөглөсөн маягтаас бүгд буруу байх магадлалыг нэмэх хэрэгтэй. Хоёр дахь үйл явдлын магадлал
Ийнхүү бөглөсөн дөрвөн маягтын дотроос гурваас доошгүй нь буруу байх магадлал тэнцүү байна
P(X > 3) = P(X = 3) + P(X = 4) = 0.0036 + 0.0001 = 0.0037
3. Маягтыг буруу бөглөх магадлалыг 0.1 гэж үзье. Дөрвөн бөглөсөн маягтаас гурваас бага нь буруу байх магадлал хэд вэ? Энэ үйл явдлын магадлал
P(X< 3) = P(X = 0) + P(X = 1) + P(X = 2)
Томъёо (2) ашиглан бид эдгээр магадлал тус бүрийг тооцоолно.

Тиймээс P(X< 3) = 0,6561 + 0,2916 + 0,0486 = 0,9963.
Магадлал P(X< 3) можно вычислить иначе. Для этого воспользуемся тем, что событие X < 3 является дополнительным по отношению к событию Х>3. Дараа нь P(X< 3) = 1 – Р(Х> 3) = 1 – 0,0037 = 0,9963.
Түүврийн хэмжээ нэмэгдэх тусам n 3-р жишээнд хийсэн тооцоололтой төстэй тооцоо хийхэд хэцүү болно. Эдгээр хүндрэлээс зайлсхийхийн тулд олон тооны бином магадлалыг урьдчилан хүснэгтэд үзүүлэв. Эдгээр магадлалын заримыг Зураг дээр үзүүлэв. 1. Жишээ нь, магадлалыг авахын тулд X= 2 цагт n= 4 ба х= 0.1, та шугамын огтлолцол дээрх тоог хүснэгтээс гаргаж авах хэрэгтэй X= 2 ба багана r = 0,1.

Цагаан будаа. 1. Хоёрдахь магадлал at n = 4, X= 2 ба r = 0,1
Хоёр нэрийн тархалтыг Excel-ийн =BINOM.DIST() функцийг ашиглан тооцоолж болно (Зураг 2), 4 параметртэй: амжилтын тоо - X, туршилтын тоо (эсвэл түүврийн хэмжээ) - n, амжилтанд хүрэх магадлал - r, параметр интеграл, энэ нь ҮНЭН утгыг авдаг (энэ тохиолдолд магадлалыг тооцоолно дутуугүй Xүйл явдал) эсвэл ХУДАЛ (энэ тохиолдолд магадлалыг тооцно яг Xүйл явдал).

Цагаан будаа. 2. Функцийн параметрүүд =BINOM.DIST()
Дээрх гурван жишээний хувьд тооцооллыг Зураг дээр үзүүлэв. 3 (мөн Excel файлыг үзнэ үү). Багана бүр нэг томъёог агуулна. Тоонууд нь харгалзах тооны жишээнүүдийн хариултыг харуулж байна).

Цагаан будаа. 3. Excel-д хоёрт тархалтын тооцоо n= 4 ба х = 0,1
Бином тархалтын шинж чанарууд
Бином тархалт нь параметрээс хамаарна nТэгээд r. Бином тархалт нь тэгш хэмтэй эсвэл тэгш бус байж болно. Хэрэв p = 0.05 бол параметрийн утгаас үл хамааран бином тархалт тэгш хэмтэй байна. n. Харин p ≠ 0.05 бол тархалт хазайсан болно. Яаж илүү ойр үнэ цэнэпараметр r 0.05 хүртэл, түүврийн хэмжээ их байх тусам n, хуваарилалтын тэгш бус байдал бага байх тусам. Тиймээс буруу бөглөсөн маягтын тоог хуваарилах нь баруун тийш хазайсан тул х= 0.1 (Зураг 4).

Цагаан будаа. 4. Хоёр тоот тархалтын гистограмм n= 4 ба х = 0,1
Бином тархалтын хүлээлтдээжийн хэмжээтэй бүтээгдэхүүнтэй тэнцүү байна nамжилтанд хүрэх магадлалын талаар r:
(3) M = E(X) =n.p.
Дунджаар, дөрвөн дарааллаас бүрдсэн дээж дэх хангалттай урт цуврал туршилтууд нь p = E(X) = 4 x 0.1 = 0.4 буруу бөглөсөн маягт байж болно.
Бином тархалтын стандарт хазайлт
Жишээлбэл, стандарт хазайлтнягтлан бодох бүртгэлд буруу бөглөсөн маягтын тоо мэдээллийн системтэнцүү байна:
Левин нар Менежерүүдэд зориулсан статистик номны материалыг ашигласан. – М.: Уильямс, 2004. – х. 307–313
Бүх юмс үзэгдлийг 1, 2, 3... 100500... гэх мэт тоон хэмжүүрээр хэмждэггүй. Аливаа үзэгдэл үргэлж хязгааргүй эсвэл олон тооны янз бүрийн төлөвийг авч чаддаггүй. Жишээлбэл, хүний хүйс нь M эсвэл F байж болно. Буудагч нь бай онох эсвэл алдаж байна. Та "Тэмдэг" эсвэл "эсрэг" гэх мэт санал өгөх боломжтой. гэх мэт. Өөрөөр хэлбэл, ийм өгөгдөл нь өөр шинж чанарын төлөвийг илэрхийлдэг - "тийм" (үйл явдал болсон) эсвэл "үгүй" (үйл явдал болоогүй). Болж буй үйл явдлыг (эерэг үр дүн) мөн "амжилт" гэж нэрлэдэг.
Ийм өгөгдөлтэй туршилтыг дууддаг Бернулли схем, олон тооны туршилтаар эерэг үр дүнг нийт туршилтын тоонд харьцуулсан харьцаа нь энэ үйл явдлын магадлалд чиглэгддэг болохыг олж мэдсэн Швейцарийн алдарт математикчийг хүндэтгэн тэмдэглэв.
Альтернатив шинж чанарын хувьсагч
Шинжилгээнд математикийн төхөөрөмжийг ашиглахын тулд ийм ажиглалтын үр дүнг тэмдэглэнэ тоон хэлбэр. Үүнийг хийхийн тулд эерэг үр дүнд 1-ийн тоо, сөрөг үр дүн - 0. Өөрөөр хэлбэл, бид зөвхөн хоёр утгыг авах боломжтой хувьсагчтай харьцаж байна: 0 эсвэл 1.
Үүнээс ямар ашиг тус авч болох вэ? Ер нь энгийн мэдээллээс дутахгүй. Тиймээс эерэг үр дүнгийн тоог тооцоолоход хялбар байдаг - бүх утгыг нэгтгэн дүгнэхэд хангалттай, жишээлбэл. бүгд 1 (амжилт). Та цааш явж болно, гэхдээ энэ нь танд хэд хэдэн тэмдэглэгээг нэвтрүүлэх шаардлагатай болно.
Анхаарах зүйл бол эерэг үр дүн (энэ нь 1-тэй тэнцүү) гарах магадлал багатай байдаг. Жишээлбэл, зоос шидэх үед толгой авах нь ½ эсвэл 0.5 байна. Энэ магадлалыг уламжлал ёсоор латин үсгээр тэмдэглэдэг х. Тиймээс альтернатив үйл явдлын магадлал нь тэнцүү байна 1 - х, үүнийг мөн тэмдэглэдэг q, тэр нь q = 1 – х. Эдгээр тэмдэглэгээг хувьсах хуваарилалтын хүснэгт хэлбэрээр тодорхой системчилж болно X.
Бид боломжит утгууд болон тэдгээрийн магадлалын жагсаалтыг хүлээн авсан. Тооцоолж болно математикийн хүлээлт Тэгээд тархалт. Хүлээлт нь бүх боломжит утгуудын бүтээгдэхүүний нийлбэр ба тэдгээрийн харгалзах магадлал юм.
![]()
Дээрх хүснэгтүүдийн тэмдэглэгээг ашиглан хүлээлтийг тооцоолъё.
Альтернатив тэмдгийн математикийн хүлээлт нь энэ үйл явдлын магадлалтай тэнцүү байна. х.
Одоо альтернатив шинж чанарын хэлбэлзэл гэж юу болохыг тодорхойлъё. Тархалт гэдэг нь математикийн хүлээлтээс хазайсан дундаж квадрат юм. Ерөнхий томъёо(дискрет өгөгдлийн хувьд) дараах хэлбэртэй байна:
Тиймээс альтернатив шинж чанарын хэлбэлзэл:

Энэ тархалт хамгийн ихдээ 0.25 ( p=0.5).
Стандарт хазайлт нь дисперсийн үндэс юм:
Хамгийн их утга нь 0.5-аас хэтрэхгүй.
Таны харж байгаагаар математикийн хүлээлт ба альтернатив шинж чанарын дисперс нь маш нягт хэлбэртэй байдаг.
Санамсаргүй хэмжигдэхүүний бином тархалт
Нөхцөл байдлыг өөр өнцгөөс харцгаая. Үнэхээр нэг шидэхэд толгойн дундаж алдагдал 0.5 байх нь хэнд хамаатай юм бэ? Төсөөлөх ч боломжгүй. Өгөгдсөн тооны шидэлтийн хувьд хэдэн толгой гарч ирдэг талаар асуулт асуух нь илүү сонирхолтой юм.
Өөрөөр хэлбэл, судлаач тодорхой тооны амжилттай үйл явдал тохиолдох магадлалыг ихэвчлэн сонирхдог. Энэ нь шалгасан багц дахь гэмтэлтэй бүтээгдэхүүний тоо (1 - гэмтэлтэй, 0 - сайн) эсвэл эдгэрэлтийн тоо (1 - эрүүл, 0 - өвчтэй) гэх мэт байж болно. Ийм "амжилтын" тоо нь хувьсагчийн бүх утгуудын нийлбэртэй тэнцүү байх болно X, өөрөөр хэлбэл ганц үр дүнгийн тоо.
Санамсаргүй хувьсагч Ббином гэж нэрлэгддэг ба 0-ээс утгыг авна n(цагт Б= 0 – бүх хэсгүүд тохиромжтой, хамт Б = n– бүх эд анги гэмтэлтэй). Энэ нь бүх үнэт зүйлс гэж үздэг xбие биенээсээ хараат бус. Хоёр тоот хувьсагчийн үндсэн шинж чанарыг авч үзье, өөрөөр хэлбэл бид түүний математик хүлээлт, тархалт, тархалтыг тогтоох болно.
Хоёр тоот хувьсагчийн хүлээлтийг олж авахад маш хялбар байдаг. Хэмжигдэхүүний нийлбэрийн математик хүлээлт нь нэмсэн хэмжигдэхүүн бүрийн математик хүлээлтийн нийлбэр бөгөөд энэ нь хүн бүрт ижил байдаг тул:
Жишээлбэл, 100 удаа шидэгдсэн толгойн тоог математикийн хүлээлт 100 × 0.5 = 50 байна.
Одоо бид хоёрт хувьсагчийн дисперсийн томъёог гаргаж авлаа. Бие даасан санамсаргүй хэмжигдэхүүний нийлбэрийн дисперс нь хэлбэлзлийн нийлбэр юм. Эндээс
Стандарт хазайлт тус тус
100 зоос шидэхэд толгойн тооны стандарт хазайлт нь байна
Эцэст нь дуран утгын тархалтыг авч үзье, i.e. санамсаргүй хэмжигдэхүүн байх магадлал Бөөр өөр үнэ цэнийг авах болно к, Хаана 0≤k≤n. Зоосны хувьд энэ асуудал дараах байдлаар харагдаж болно: 100 шидэхэд 40 толгой авах магадлал хэд вэ?
Тооцооллын аргыг ойлгохын тулд зоосыг ердөө 4 удаа шидсэн гэж төсөөлөөд үз дээ. Аль ч тал нь хэзээ ч унаж болно. Бид өөрөөсөө 4 шидэлтээс 2 толгой авах магадлал хэд вэ гэж асуудаг. Шидэлт бүр бие биенээсээ хамааралгүй. Энэ нь аливаа хослолыг авах магадлал нь шидэлт бүрийн өгөгдсөн үр дүнгийн магадлалын үржвэртэй тэнцүү байна гэсэн үг юм. O толгойнууд, P нь сүүлтэй байг. Жишээлбэл, бидэнд тохирсон хослолуудын нэг нь OOPP шиг харагдаж болно, өөрөөр хэлбэл:

Ийм хослолын магадлал нь толгой авах хоёр магадлал ба толгой авахгүй байх хоёр магадлалын үржвэртэй тэнцүү байна (урвуу үйл явдлыг дараах байдлаар тооцно. 1 - х), i.e. 0.5×0.5×(1-0.5)×(1-0.5)=0.0625. Энэ нь бидэнд тохирсон хослолуудын аль нэгний магадлал юм. Гэхдээ асуулт нь ямар нэг тодорхой дарааллын тухай биш нийт бүргэдийн тоо байсан юм. Дараа нь та яг 2 толгойтой бүх хослолын магадлалыг нэмэх хэрэгтэй. Тэд бүгд адилхан (хүчин зүйл өөрчлөгдөхөд бүтээгдэхүүн өөрчлөгдөхгүй) нь ойлгомжтой. Тиймээс та тэдгээрийн тоог тооцоолж, дараа нь ийм хослолын магадлалаар үржүүлэх хэрэгтэй. RROO, RORO, ROOR, ORRO, OROR, OORR гэсэн 2 толгойтой 4 шидэлтийн бүх хослолыг тоолж үзье. Нийтдээ 6 сонголт байна.

Тиймээс 4 шидэлтийн дараа 2 толгой авахыг хүссэн магадлал 6×0,0625=0,375 байна.
Гэсэн хэдий ч ингэж тоолох нь уйтгартай юм. Аль хэдийн 10 зоосны хувьд нийт сонголтуудын тоог харгис хүчээр олж авахад маш хэцүү байх болно. Тийм ч учраас ухаалаг хүмүүс-ийн янз бүрийн хослолын тоог тооцоолох томьёог эртнээс зохион бүтээжээ nэлементүүд к, Хаана n- нийт элементийн тоо; к– зохион байгуулалтын сонголтуудыг тооцсон элементүүдийн тоо. -ийн хослолын томъёо nэлементүүд кэнэ нь:
![]()
Комбинаторик хэсэгт үүнтэй төстэй зүйл тохиолддог. Тэнд мэдлэгээ дээшлүүлэхийг хүссэн хүн бүрийг явуулна. Эндээс дурдвал, хоёр гишүүний тархалтын нэр (дээрх томъёо нь Ньютоны биномийн тэлэлтийн коэффициент юм).
Магадлалыг тодорхойлох томъёог ямар ч хэмжигдэхүүнд хялбархан ерөнхийлж болно nТэгээд к. Үүний үр дүнд бином тархалтын томъёо дараах хэлбэртэй байна.
Нөхцөлд нийцсэн хослолын тоог тэдгээрийн аль нэгнийх нь магадлалаар үржүүлнэ.
Практикт ашиглахын тулд бином тархалтын томъёог мэдэхэд л хангалттай. Эсвэл та мэдэхгүй байж магадгүй - доор бид Excel ашиглан магадлалыг хэрхэн тодорхойлохыг харуулав. Гэхдээ мэдэх нь дээр.
Энэ томъёог ашиглан бид 100 шидэхэд 40 толгой авах магадлалыг тооцоолно.
Эсвэл ердөө 1.08%. Харьцуулбал, энэ туршилтын математикийн хүлээлт, өөрөөр хэлбэл 50 толгой байх магадлал 7.96% байна. Хоёр тоот утгын хамгийн их магадлал нь математикийн хүлээлттэй харгалзах утгад хамаарна.
Excel дээр хоёр нэрийн тархалтын магадлалыг тооцоолох
Хэрэв та зөвхөн цаас, тооцоолуур ашигладаг бол интеграл байхгүй ч бином тархалтын томъёог ашиглан тооцоо хийх нь нэлээд хэцүү байдаг. Жишээлбэл, утга нь 100 байна! - 150 гаруй тэмдэгттэй. Өмнө нь, одоо ч гэсэн ийм хэмжигдэхүүнийг тооцоолохын тулд ойролцоогоор томъёог ашигладаг байсан. Одоогийн байдлаар MS Excel гэх мэт тусгай програм хангамжийг ашиглахыг зөвлөж байна. Тиймээс дурын хэрэглэгч (сургалттай хүмүүнлэг ч гэсэн) хоёр тоогоор тархсан санамсаргүй хэмжигдэхүүний утгын магадлалыг хялбархан тооцоолж чадна.
Материалыг нэгтгэхийн тулд бид Excel-ийг ердийн тооцоолуур болгон ашиглах болно, жишээлбэл. Хоёр тоот тархалтын томъёог ашиглан алхам алхмаар тооцооллыг хийцгээе. Жишээлбэл, 50 толгой авах магадлалыг тооцоолъё. Тооцооллын үе шат, эцсийн үр дүн бүхий зургийг доор харуулав.

Таны харж байгаагаар завсрын үр дүн нь хаа сайгүй хэрэглэгддэг ч эсийн дотор багтахгүй хэмжээтэй байна. энгийн функцуудтөрөл: FACTOR (факторын тооцоо), POWER (тоог зэрэглэлд хүргэх), түүнчлэн үржүүлэх, хуваах операторууд. Түүнээс гадна, энэ тооцоо нь ямар ч тохиолдолд маш төвөгтэй, учир нь энэ нь нягт биш юм; олон эсүүд оролцдог. Тийм ээ, тэр даруй ойлгоход хэцүү байдаг.
Ерөнхийдөө Excel нь бином тархалтын магадлалыг тооцоолоход бэлэн функцээр хангадаг. Функцийг дууддаг BINOM.DIST.

Амжилтын тоо - амжилттай тестийн тоо. Бидэнд 50 ширхэг бий.
Туршилтын тоо - шидэлтийн тоо: 100 удаа.
Амжилтанд хүрэх магадлал – нэг шидэхэд толгой гарах магадлал 0.5 байна.
Интеграл – 1 эсвэл 0 гэж заасан бол магадлалыг тооцно P(B=k); хэрэв 1 бол бином тархалтын функцийг тооцоолно, өөрөөр хэлбэл. -аас гарах бүх магадлалын нийлбэр B=0руу B=kбагтаасан.
OK дарж дээрхтэй ижил үр дүнг авна, зөвхөн бүх зүйлийг нэг функцээр тооцоолсон.

Маш тохиромжтой. Туршилт хийхийн тулд сүүлийн параметр 0-ийн оронд бид 1-ийг тавьдаг. Бид 0.5398-ыг авдаг. Энэ нь 100 зоос шидэхэд 0-ээс 50 хүртэлх оноо авах магадлал бараг 54% гэсэн үг юм. Гэхдээ эхлээд 50 хувь байх ёстой юм шиг санагдсан. Ерөнхийдөө тооцооллыг хурдан бөгөөд хялбархан хийдэг.
Жинхэнэ шинжээч нь функц хэрхэн ажилладагийг (түүний тархалт гэж юу вэ) ойлгох ёстой, тиймээс бид 0-ээс 100 хүртэлх бүх утгын магадлалыг тооцоолох болно. Өөрөөр хэлбэл, бид нэг толгой байхгүй байх магадлал хэд вэ гэсэн асуултыг тавих болно. 2, 3, 50, 90 эсвэл 100 гэсэн 1 бүргэд гарч ирнэ. Тооцооллыг дараах зурагт үзүүлэв. Цэнхэр шугам нь өөрөө бином тархалт, улаан цэг нь тодорхой тооны амжилтын магадлал юм.

Хоёр гишүүний тархалттай төстэй эсэхийг хэн нэгэн асууж магадгүй ... Тийм ээ, маш төстэй. Мойвр (1733 онд) хүртэл том дээж бүхий бином тархалт ойртож байна (тэр үед үүнийг юу гэж нэрлэж байсныг би мэдэхгүй) гэж хэлсэн боловч хэн ч түүнийг сонссонгүй. Гаусс, дараа нь 60-70 жилийн дараа Лаплас л дахин нээгдэж, сайтар судалжээ. ердийн хуульхуваарилалт. Математикийн хүлээлтэд хамгийн их магадлал унадаг, түүнээс хазайх тусам огцом буурч байгааг дээрх график тодорхой харуулж байна. Ердийн хууль шиг.
бином тархалт их байна практик ач холбогдол, нэлээд олон удаа тохиолддог. Excel ашиглан тооцооллыг хурдан бөгөөд хялбархан хийдэг.
Бернулли схемийн хэрэгжилтийг авч үзье, i.e. Хэд хэдэн бие даасан туршилтыг давтан хийдэг бөгөөд тус бүрт өгөгдсөн А үйл явдал нь туршилтын дугаараас үл хамааран ижил магадлалтай байна. Туршилт бүрийн хувьд зөвхөн хоёр үр дүн байдаг:
1) А үйл явдал - амжилт;
2) үйл явдал - бүтэлгүйтэл,
тогтмол магадлал бүхий
Х дискрет санамсаргүй хэмжигдэхүүнийг авч үзье - “А үйл явдлын тохиолдлын тоо. nтестүүд" гэж үзээд энэ санамсаргүй хэмжигдэхүүний тархалтын хуулийг ол. X утга нь дараах утгыг авч болно.
Магадлал ![]() санамсаргүй хэмжигдэхүүн X утгыг авна х кБернуллигийн томъёогоор олно
санамсаргүй хэмжигдэхүүн X утгыг авна х кБернуллигийн томъёогоор олно
Бернулли (1) томъёогоор тодорхойлогдсон дискрет санамсаргүй хэмжигдэхүүний тархалтын хуулийг нэрлэнэ бином тархалтын хууль. Байнгын n Тэгээд r (q=1-p)(1) томъёонд орсон , гэж нэрлэдэг бином тархалтын параметрүүд.
Тэгш байдлын баруун гар тал нь (1) нь Ньютоны биномийн өргөтгөлийн ерөнхий нэр томъёо, өөрөөр хэлбэл, "хонотын тархалт" гэсэн нэршилтэй холбоотой юм.
(2)
Тэгээд тэрнээс хойш p+q=1, тэгвэл тэгш байдлын баруун тал (2) нь 1-тэй тэнцүү байна
Энэ нь гэсэн үг
 (4)
(4)
Тэгш байдлаар (3) эхний нэр томъёо qnбаруун талд байх магадлалыг илэрхийлнэ nтестүүд, А үйл явдал нэг удаа ч гарч ирэхгүй, хоёр дахь хугацаа ![]() А үйл явдал нэг удаа гарах магадлал, гурав дахь гишүүн нь А үйл явдал хоёр удаа гарах магадлал, эцэст нь сүүлчийн гишүүн r p- А үйл явдал яг тохиолдох магадлал nнэг удаа.
А үйл явдал нэг удаа гарах магадлал, гурав дахь гишүүн нь А үйл явдал хоёр удаа гарах магадлал, эцэст нь сүүлчийн гишүүн r p- А үйл явдал яг тохиолдох магадлал nнэг удаа.
Дискрет санамсаргүй хэмжигдэхүүний тархалтын бином хуулийг хүснэгт хэлбэрээр үзүүлэв.
| X | 0 | 1 | … | к | … | n |
| Р | qn | … | … | r p |
Үндсэн тоон шинж чанарбином тархалт:
1) математикийн хүлээлт ![]() (5)
(5)
2) тархалт ![]() (6)
(6)
3) стандарт хазайлт ![]() (7)
(7)
4) үйл явдлын тохиолдлын хамгийн их магадлалтай тоо k 0- энэ нь өгөгдсөн тоо юм nхамгийн их бином магадлалд тохирч байна
Өгөгдсөнийхөө төлөө nТэгээд rЭнэ тоог тэгш бус байдлаар тодорхойлно
![]() (8)
(8)
тоо бол pr+rбүхэлдээ биш, тэгвэл k 0энэ тооны бүхэл хэсэгтэй тэнцүү, хэрэв pr+rнь бүхэл тоо юм k 0гэсэн хоёр утгатай
Магадлалын тархалтын бином хуулийг буудлагын онол, статистик бүтээгдэхүүний чанарын хяналтын онол, практикт, дарааллын онол, найдвартай байдлын онол гэх мэтэд ашигладаг. Энэ хуулийг бие даасан шалгалтын дараалал байгаа бүх тохиолдолд хэрэглэж болно.
Жишээ 1:Чанарын туршилтаар 100 төхөөрөмж тутмын 90 нь гэмтэл согоггүй болохыг тогтоожээ. Санамсаргүй байдлаар худалдаж авсан өндөр чанартай төхөөрөмжүүдийн тооны магадлалын тархалтын бином хуулийг зурна уу 4.
Шийдэл:Үүссэн эсэхийг шалгаж буй А үйл явдал нь "санамсаргүй байдлаар худалдаж авсан өндөр чанартай төхөөрөмж" юм. Асуудлын нөхцлийн дагуу бином тархалтын үндсэн параметрүүд нь:
Санамсаргүй хэмжигдэхүүн X нь авсан 4 төхөөрөмжөөс өндөр чанартай төхөөрөмжүүдийн тоо бөгөөд энэ нь X-ийн утгыг илэрхийлдэг - (1) томъёог ашиглан X-ийн утгын магадлалыг олцгооё:

Тиймээс X утгын тархалтын хууль нь авсан 4 төхөөрөмжөөс өндөр чанартай төхөөрөмжийн тоо юм.
| X | 0 | 1 | 2 | 3 | 4 |
| Р | 0,0001 | 0,0036 | 0,0486 | 0,2916 | 0,6561 |
Түгээлтийн барилгын зөв эсэхийг шалгахын тулд магадлалын нийлбэр хэдтэй тэнцүү болохыг шалгая.
Хариулт:Хуваарилалтын хууль
| X | 0 | 1 | 2 | 3 | 4 |
| Р | 0,0001 | 0,0036 | 0,0486 | 0,2916 | 0,6561 |
Жишээ 2:Хэрэглэсэн эмчилгээний арга нь 95% -д эдгэрэхэд хүргэдэг. Таван өвчтөн энэ аргыг ашигласан. Эдгэрсэн хүмүүсийн хамгийн их магадлалтай тоог, мөн санамсаргүй хэмжигдэхүүн X-ийн тоон шинж чанарыг олоорой - энэ аргыг хэрэглэсэн 5 өвчтөнөөс эдгэрсэн хүмүүсийн тоог.
Дуран тархалт нь салангид хэлбэлзэлтэй санамсаргүй хэмжигдэхүүний хамгийн чухал магадлалын тархалтын нэг юм. Дуран тархалт нь тухайн тооны магадлалын тархалт юм мүйл явдал тохиолдох АВ nхарилцан бие даасан ажиглалт. Ихэнхдээ үйл явдал ААжиглалтын "амжилт" гэж нэрлэдэг бөгөөд эсрэг үйл явдлыг "бүтэлгүйт" гэж нэрлэдэг боловч энэ тэмдэглэгээ нь маш нөхцөлтэй байдаг.
Бином тархалтын нөхцөл:
- нийт гүйцэтгэсэн nүйл явдал болсон шүүх хурал Атохиолдож болно, үгүй ч байж болно;
- үйл явдал Атуршилт бүрт ижил магадлалтай тохиолдож болно х;
- тестүүд бие биенээсээ хараат бус байдаг.
Үүнд орох магадлал nтуршилтын үйл явдал Аяг ирэх болно мудаа Бернуллигийн томъёогоор тооцоолж болно:
![]()
Хаана х- үйл явдал болох магадлал А;
q = 1 - х- эсрэг үйл явдал тохиолдох магадлал.
Үүнийг олж мэдье Яагаад хоёр нэрийн тархалт Бернуллигийн томьёотой дээр дурдсан аргаар холбоотой байдаг вэ? . Үйл явдал - амжилтын тоо nТуршилтууд нь хэд хэдэн хувилбарт хуваагддаг бөгөөд тэдгээр нь тус бүрт амжилтанд хүрдэг мтуршилт, болон бүтэлгүйтэл - онд n - мтуршилтууд. Эдгээр сонголтуудын аль нэгийг авч үзье - Б1 . Магадлалыг нэмэх дүрмийг ашиглан бид эсрэг үйл явдлын магадлалыг үржүүлнэ.
![]() ,
,
мөн хэрэв бид тэмдэглэвэл q = 1 - х, Тэр
![]() .
.
Ямар ч өөр сонголт мамжилт ба n - мбүтэлгүйтэл. Ийм сонголтуудын тоо нь аль болох боломжтой аргуудын тоотой тэнцүү байна nтест авах мамжилт.
Бүх магадлалын нийлбэр мүйл явдлын тоо А(0-ээс эхлэн тоо n) нэгтэй тэнцүү байна:

Энд нэр томьёо бүр нь Ньютоны бином дахь нэр томъёог илэрхийлдэг. Тиймээс авч үзэж буй тархалтыг бином тархалт гэж нэрлэдэг.
Практикт магадлалыг "илүү ихгүй" тооцоолох шаардлагатай байдаг мамжилт nтестүүд" эсвэл "наад зах нь мамжилт nтест". Үүнд дараах томьёог ашиглана.
Интеграл функц, өөрөөр хэлбэл магадлал Ф(м) юу байна nажиглалтын үйл явдал Адахиад ирэхгүй мнэг удаа, дараах томъёогоор тооцоолж болно.
Эргээд магадлал Ф(≥м) юу байна nажиглалтын үйл явдал Абагагүй ирэх болно мнэг удаа, дараах томъёогоор тооцоолно.
Заримдаа магадлалыг тооцоолох нь илүү тохиромжтой байдаг nажиглалтын үйл явдал Адахиад ирэхгүй мэсрэг үйл явдлын магадлалаар дамжуулан:
![]() .
.
Аль томьёог ашиглах нь тэдгээрийн аль нь цөөн нэр томъёо агуулсан нийлбэрээс хамаарна.
Хоёр нэрийн тархалтын шинж чанарыг дараах томъёогоор тооцоолно .
Математикийн хүлээлт: .
Тархалт: .
MS Excel программ дээрх биномын тархалт ба тооцоолол
Бином магадлал П n ( м) ба интеграл функцийн утгууд Ф(м) MS Excel-ийн BINOM.DIST функцийг ашиглан тооцоолж болно. Харгалзах тооцоо хийх цонхыг доор харуулав (зүүн товшоод томруулна уу).

MS Excel нь дараах өгөгдлийг оруулахыг шаарддаг.
- амжилтын тоо;
- туршилтын тоо;
- амжилтанд хүрэх магадлал;
- интеграл - логикийн утга: 0 - хэрэв та магадлалыг тооцоолох шаардлагатай бол П n ( м) ба 1 - хэрэв магадлал бол Ф(м).
Жишээ 1.Компанийн менежер сүүлийн 100 хоногт зарагдсан камерын талаарх мэдээллийг нэгтгэн танилцууллаа. Хүснэгтэд мэдээллийг нэгтгэж, өдөрт тодорхой тооны камер зарагдах магадлалыг тооцсон болно.
13 ба түүнээс дээш камер зарагдсан тохиолдолд өдөр нь ашигтайгаар дуусдаг. Өдөр нь ашигтай ажиллах магадлал:
![]()
Нэг өдөр ашиггүй ажиллах магадлал:
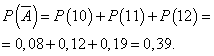
Өдөрт ашиг орлоготой ажиллах магадлал тогтмол бөгөөд 0.61-тэй тэнцүү байх ба өдөрт зарагдсан камерын тоо тухайн өдрөөс хамаарахгүй. Дараа нь бид үйл явдал болох бином тархалтыг ашиглаж болно А- өдөр ашигтай ажиллана, - ашиггүй.
6 өдрийн турш ашиг олох магадлал:
![]() .
.
Бид MS Excel-ийн BINOM.DIST функцийг ашиглан ижил үр дүнг авдаг (интеграл утгын утга нь 0):
П 6 (6 ) = BINOM.DIST(6; 6; 0.61; 0) = 0.052.
6 хоногоос 4 ба түүнээс дээш хоног ашиг орлоготой ажиллах магадлал:
Хаана ![]() ,
,
![]() ,
,
MS Excel-ийн BINOM.DIST функцийг ашиглан бид 6 хоногоос 3 хоногоос илүүгүй хугацаанд ашиг олох магадлалыг тооцоолно (интеграл утгын утга нь 1):
П 6 (≤3 ) = BINOM.DIST(3; 6; 0.61; 1) = 0.435.
Бүх 6 хоног алдагдалтай ажиллах магадлал:
![]() ,
,
Бид MS Excel-ийн BINOM.DIST функцийг ашиглан ижил үзүүлэлтийг тооцоолж болно.
П 6 (0 ) = BINOM.DIST(0; 6; 0.61; 0) = 0.0035.
Асуудлыг өөрөө шийдэж, дараа нь шийдлийг хар
Жишээ 2.Цүнхэнд 2 цагаан, 3 хар бөмбөг байна. Бөмбөгийг савнаас гаргаж аваад өнгийг нь тохируулаад буцааж тавина. оролдлого 5 удаа давтана. Цагаан бөмбөлгүүдийн тохиолдлын тоо нь салангид санамсаргүй хэмжигдэхүүн юм X, бином хуулийн дагуу тархсан. Санамсаргүй хэмжигдэхүүний тархалтын хуулийг зур. Горим, математикийн хүлээлт, тархалтыг тодорхойлох.
Хамтдаа асуудлыг шийдье
Жишээ 3.Шуудангийн үйлчилгээнээс бид сайтууд руу явлаа n= 5 шуудан зөөгч. Илгээгч бүр магадлалтай х= 0.3 бусдаас үл хамааран объектоос хоцорсон. Дискрет санамсаргүй хэмжигдэхүүн X- хоцорсон шуудангийн тоо. Энэ санамсаргүй хэмжигдэхүүний тархалтын цувралыг байгуул. Түүний математик хүлээлт, дисперс, стандарт хазайлтыг ол. Хамгийн багадаа хоёр шуудан зөөгч объектуудаас хоцрох магадлалыг ол.