Спектральное представление временных функций широко используется в теории связи. Для теоретических и экспериментальных исследований характеристик электрических цепей и передачи сообщений по каналам связи используется различные типы сигналов: гармонические колебания, уровни постоянных напряжений, последовательности прямоугольных и радиоимпульсов и т. д. Особо важную роль в теоретических исследованиях электрических цепей играют вычислительные сигналы в форме единичной функции и импульсной функции (функции Дирака). Определим спектры наиболее распространенных типовых сигналов.
11.1 Спектр последовательности прямоугольных импульсов
Пусть имеется периодическая последовательность импульсов прямоугольной формы периодом Т длительностью импульсов t и и амплитудой А. Аналитическое выражение функции , описывающей импульс на отрезке , имеет вид
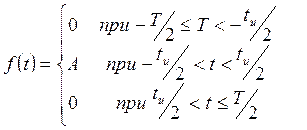(11.1)
График периодической последовательности импульсов изображен на рисунке 11.1.
Рисунок 11.1
Данная функция является четной, так как ее график симметричен относительно оси ординат. Тогда коэффициенты Фурье это функции вычисляются по формулам (КФТ2), где .
Число представляет собой среднее значение функции за период и называется постоянной составляющей. Частоту называют основной, или первой гармоникой, а частоты k высшими гармониками, где k=2,3,4,…
Построим амплитудный спектр рассматриваемой последовательности прямоугольных импульсов. Так как функция периодическая, то ее амплитудный спектр является линейчатым. Обозначим через расстояние между любыми соседними гармониками. Очевидно, оно равно . Амплитуда k-ой гармоники согласно (11.2) имеет вид
(11.3)
Найдем отношение между периодом Т и длительностью импульса , при котором амплитуда k-ой гармоники обращается в нуль.
А 2 ≈32В, А 3 ≈15В, А 4 ≈0, А 5 ≈6,36В, А 6 ≈10,5В, А 7 ≈6,36В, А 8 ≈0, А 9 ≈4,95В, А 10 ≈6,37В.
Полученный в результате расчета амплитудный спектр приведен на рисунке 11.2.
Рисунок 11.2
Такой спектр называют линейчатым или дискретным спектром.
Аналогично рассчитаны и построены спектры для q=8 и q=16. Они приведены на рисунках 11.3 и 11.4 соответственно.
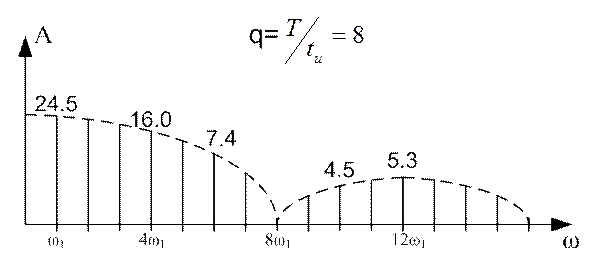
Рисунок 11.3
Рисунок 11.4
Из рисунка видно, что чем больше скважность прямоугольных импульсов, тем меньше значение имеет амплитуда первой гармоники, но тем медленнее убывает спектр.
11.2 Спектр одиночного прямоугольного импульса
Рассмотрим Ф (11.1) для случая, когда Т→∞, то есть периодическая последовательность импульсов вырождается в одиночный прямоугольный импульс, длительностью t u .
Аналитическое выражение для этого импульса запишется в виде:
График этой функции изображен на рисунке 11.5.
Рисунок 11.5
В этом случае частота первой гармоники и расстояние между гармониками становится равным 0, следовательно, спектр из дискретного превращается в непрерывный, состоящий из бесконечно большого числа спектральных линий, находящихся на бесконечно малых расстояниях друг от друга. Такой спектр называют сплошным. Отсюда следует важнейшее правило: периодические сигналы порождают дискретные спектры, а непериодические – сплошные (непрерывные).
Спектр прямоугольного одиночного импульса можно найти непосредственно из прямого преобразования Фурье (10.1)
В предыдущих разделах мы рассмотрели разложение периодических сигналов в ряд Фурье, а также изучили некоторые свойства представления периодических сигналов рядом Фурье. Мы говорили, что периодические сигналы можно представить как ряд комплексных экспонент, отстоящих друг от друга на частоту рад/c, где — период повторения сигнала. В результате мы можем трактовать представление сигнала в виде ряда комплексных гармоник как комплексный спектр сигнала. Комплексный спектр, в свою очередь, может быть разделен на амплитудный и фазовый спектры периодического сигнала.В данном разделе мы рассмотрим спектр периодической последовательности прямоугольных импульсов, как одного из важнейших сигналов, используемого в практических приложениях.
Спектр периодической последовательности прямоугольных импульсов
Пусть входной сигнал представляет собой периодическую последовательность прямоугольных импульсов амплитуды , длительности секунд следующих с периодом секунд, как это показано на рисунке 1
Рисунок 1. Периодическая последовательность прямоугольных импульсов
Единица измерения амплитуды сигнала зависит от физического процесса, который описывает сигнал . Это может быть напряжение, или, сила тока, или любая другая физическая величина со своей единицей измерения, которая меняется во времени как . При этом, единицы измерения амплитуд спектра , , будут совпадать с единицами измерения амплитуды исходного сигнала.
Тогда спектр , , данного сигнала может быть представлен как:
Спектр периодической последовательности прямоугольных импульсов представляет собой множество гармоник с огибающей вида
.
Свойства спектра периодической последовательности прямоугольных импульсов
Рассмотрим некоторые свойства огибающей спектра периодической последовательности прямоугольных импульсов.
Постоянная составляющая огибающей может быть получена как предел:
Для раскрытия неопределенности воспользуемся правилом Лопиталя :
Где называется скважностью импульсов и задает отношение периода повторения импульсов к длительности одиночного импульса.
Таким образом, значение огибающей на нулевой частоте равно амплитуде импульса деленной на скважность. При увеличении скважности (т.е. при уменьшении длительности импульса при фиксированном периоде повторения) значение огибающей на нулевой частоте уменьшается.
Используя скважность импульсов выражение (1) можно переписать в виде:
Нули огибающей спектра последовательности прямоугольных импульсов можно получить из уравнения:
Знаменатель обращается в ноль только при , однако, как мы выяснили выше
, тогда решением уравнения будет
Тогда огибающая обращается в ноль если
На рисунке 2 показана огибающая спектра периодической последовательности прямоугольных импульсов (пунктирная линия) и частотные соотношения огибающей и дискретного спектра .
Рисунок 2. Cпектр периодической последовательности прямоугольных импульсов
Также показаны амплитудная огибающая , амплитудный спектр , а также фазовая огибающая и фазовый спектр .Из рисунка 2 можно заметить, что фазовый спектр принимает значения когда огибающая имеет отрицательные значения. Заметим, что и соответствуют одной и той же точке комплексной плоскости равной .
Пример спектра периодической последовательности прямоугольных импульсов
Пусть входной сигнал представляет собой периодическую последовательность прямоугольных импульсов амплитуды , следующих с периодом секунды и различной скважностью . На рисунке 3а показаны временные осциллограммы указанных сигналов, их амплитудные спектры (рисунок 3б), а также непрерывные огибающие спектров (пунктирная линия).
Рисунок 3. Cпектр периодической последовательности
прямоугольных импульсов при различном значении скважности
а — временные осциллограммы; б — амплитудный спектр
Как можно видеть из рисунка 3, при увеличении скважности сигнала, длительность импульсов уменьшается, огибающая спектра расширяется и уменьшается по амплитуде (пунктирная линия). В результате, в пределах главного лепестка увеличивается количество гармоник спектра .
Спектр смещенной во времени периодической последовательности прямоугольных импульсов
Выше мы подробно изучили спектр периодической последовательности прямоугольных импульсов для случая, когда исходный сигнал являлся симметричным относительно . В результате спектр такого сигнала является вещественным и задается выражением (1). Теперь мы рассмотрим, что произойдет со спектром сигнала если мы сместим сигнал во времени,как это показано на рисунке 4 .
Рисунок 4. Сдвинутая во времени периодическая последовательность прямоугольных импульсов
Смещенный сигнал можно представить как сигнал ,
задержанный на половину длительности импульса
.
Спектр смещенного сигнала можно представить
согласно свойству
циклического временного сдвига
как:
Таким образом, спектр периодической последовательности прямоугольных импульсов, смещенной относительно нуля, не
является чисто вещественной функцией, а приобретает дополнительный фазовый множитель
.
Амплитудный и фазовый
спектры показаны на рисунке 5.
Рисунок 5. Амплитудный и фазовый спектры сдвинутой во времени периодической последовательности прямоугольных импульсов
Из рисунка 5 следует, что сдвиг периодического сигнала во времени не изменяет амплитудный спектр сигнала, но добавляет линейную составляющую к фазовому спектру сигнала.
Выводы
В данном разделе мы получили аналитическое выражение для спектра периодической последовательности прямоугольных импульсов.
Мы рассмотрели свойства огибающей спектра периодической последовательности прямоугольных импульсов и привели примеры спектров при различном значении скважности.
Также был рассмотрен спектр при смещении во времени последовательности прямоугольных импульсов и показано, что смещение во времени изменяет фазовый спектр и не влияет на амплитудный спектр сигнала.
Москва, Советское радио, 1977, 608 c.Дёч, Г. Руководство по практическому применению преобразования Лапласа. Москва, Наука, 1965, 288 c.
Периодическая последовательность прямоугольных видеоимпульсов является модулирующей функцией для формирования периодической последовательности прямоугольных радиоимпульсов (ПППВИ), которые являются зондирующими сигналами для обнаружения и измерения координат движущихся целей. Поэтому, по спектру модулирующей функции (ПППВИ), можно относительно просто и быстро и определить спектр зондирующего сигнала (ПППРИ). При отражении зондирующего сигнала от движущейся цели изменяются частоты спектра гармоник несущего колебания (эффект Доплера). Вследствие чего, можно выделить полезный сигнал, отраженный от движущейся цели, на фоне мешающих (помеховых) колебаний, отраженных от неподвижных объектов (местные предметы) или малоподвижных объектов (метеообразования, стаи птиц и др.).
ПППВИ (рис. 1.42) представляет собой совокупность одиночных прямоугольных видеоимпульсов, следующих друг за другом через равные промежутки времени. Аналитическое выражение сигнала.
где – амплитуда импульсов; – длительность импульсов; – период следования импульсов; – частота следования импульсов, ; – скважность.
Для вычисления спектрального состава периодической последовательности импульсов применяют ряд Фурье. При известных спектрах одиночных импульсов, образующих периодическую последовательность, можно воспользоваться связью между спектральной плотностью импульсов и комплексными амплитудами ряда:
Для одиночного прямоугольного видеоимпульса спектральная плотность описывается формулой
Воспользовавшись связью между спектральной плотностью одиночного импульса и комплексными амплитудами ряда, находим
где = 0; ± 1; ± 2; ...
Амплитудно-частотный спектр (рис. 1.43) будет представлен совокупностью составляющих:
при этом положительным значениям соответствуют нулевые начальные фазы, а отрицательным – начальные фазы, равные .
Таким образом, аналитическое выражение ПППВИ будет равно
Из анализа графиков, приведенных на рисунке 1.43 следует:
· Спектр ПППВИ дискретный состоящий из отдельных гармоник с частотой .
· Огибающая АЧС изменяется по закону .
· Максимальное значение огибающей при равно , значение постоянной составляющей .
· Начальные фазы гармоник в пределах нечетных лепестков равны 0, в пределах четных .
· Количество гармоник в пределах каждого лепестка равно .
· Ширина спектра сигнала на уровне 90% энергии сигнала
· База сигнала , поэтому сигнал является простым.
Если изменять длительность импульсов , либо частоту их повторения F (период ), то параметры спектра и его АЧС будет изменяться.
На рисунке 1.43 представлен пример изменения сигнала и его АЧС при увеличении длительности импульса в два раза.
Периодические последовательности прямоугольных видеоимпульсов и их АЧС параметрами , T ,. и , T , изображены на рисунке 1.44.
Из анализа приведенных графиков следует:
1. Для ПППВИ с длительностью импульса :
· Скважность q =4, следовательно, в пределах каждого лепестка сосредоточено 3 гармоники;
· Частота k-ой гармоники ;
· Ширина спектра сигнала на уровне 90% энергии ;
· Постоянная составляющая равна
2. Для ПППВИ с длительностью импульса :
· Скважность q= 2, следовательно, в пределах каждого лепестка находится 1 гармоника;
· Частота k-ой гармоники осталось неизменной ;
· Ширина спектра сигнала на уровне 90% его энергии уменьшилась в 2 раза ;
· Постоянная составляющая увеличилась в 2 раза .
Таким образом, можно сделать вывод, что при увеличении длительности импульса, происходит “сжатие” АЧС вдоль оси ординат (уменьшается ширина спектра сигнала), при этом увеличиваются амплитуды спектральных составляющих. Частоты гармоник не изменяются.
На рисунке 1.44. представлен пример изменения сигнала и его АЧС при увеличении периода следования в 4 раза (уменьшение частоты повторения в 4 раза).
c) ширина спектра сигнала на уровне 90% его энергии не изменилась;
d) постоянная составляющая уменьшилась в 4 раза.
Таким образом, можно сделать вывод, что при увеличении периода следования (уменьшении частоты повторения происходит “сжатие ”) АЧС вдоль оси частот (уменьшаются амплитуды гармоник с увеличением их количества в пределах каждого лепестка). Ширина спектра сигнала при этом не изменяется. Дальнейшее уменьшение частоты повторения (увеличения периода следования) приведет (при ) к уменьшению амплитуд гармоник до бесконечно малых величин. При этом сигнал превратиться в одиночный, соответственно спектр станет сплошным.
Рассмотрим
периодическую последовательность
импульсов прямоугольной формы с периодом
Т, длительностью импульсов
и максимальным значением
.
Найдем разложение в ряд такого сигнала,
выбрав начало координат как показано
на рис. 15. при этом функция симметрична
относительно оси ординат, т.е. все
коэффициенты синусоидальных составляющих
=0,
и нужно рассчитать только коэффициенты
.
-
0
T
t
постоянная
составляющая
(28)
Постоянная
составляющая – это среднее значение
за период, т.е. это площадь импульса
,
деленная на весь период, т.е.
,
т.е. то же, что получилось и при строгом
формальном вычислении (28).
Вспомним,
что частота первой гармоники 1 =
,
где Т – период прямоугольного сигнала.
Расстояние между гармониками= 1 .
Если номер гармоники n
окажется таким, что аргумент синуса
,
откуда
.
Номер гармоники, при котором амплитуда
ее обращается в ноль первый раз, называют«первым
нулем»
и
обозначают его буквой N,
подчеркивая особые свойства этой
гармоники:
(29)
с
другой стороны, скважность S
импульсов – это отношение периода Т к
длительности импульсов t u ,
т.е.
.
Следовательно «первый нуль» численно
равен скважности импульсаN
=
S
.
Поскольку синус обращается в ноль при
всех значениях аргумента, кратных ,
то и амплитуды всех гармоник с номерами,
кратными номеру «первого нуля», тоже
обращаются в ноль. То есть
при
,
гдеk
– любое целое число. Так, например, из
(22) и (23) следует, что спектр прямоугольных
импульсов со скважностью 2 состоит
только из нечетных гармоник. Поскольку
S
=2
,
то и N
=2
,
т.е. амплитуда второй гармоники первый
раз обращается в ноль – это «первый
нуль». Но тогда и амплитуды всех остальных
гармоник с номерами, кратными 2, т.е. все
четные тоже должны обращаться в ноль.
При скважности S=3
нулевые амплитуды будут у 3, 6, 9, 12,
….гармоник.
С увеличением скважности «первый нуль» смещается в область гармоник с большими номерами и, следовательно, скорость убывания амплитуд гармоник уменьшается. Простой расчет амплитуды первой гармоники при U m =100В для скважности S =2, U m 1 =63,7B, при S =5, U m 1 =37,4B и при S =10, U m 1 =19,7B, т.е. с ростом скважности амплитуда первой гармоники резко уменьшается. Если же найти отношение амплитуды, например, 5-й гармоники U m 5 к амплитуде первой гармоники U m 1 , то для S =2, U m 5 /U m 1 =0,2, а для S =10, U m 5 / U m 1 = 0,9, т.е. скорость затухания высших гармоник с ростом скважности уменьшается.
Таким образом, с ростом скважности спектр последовательности прямоугольных импульсов становится более равномерным.
2.5. Спектры при уменьшении длительности импульса и периода сигнала.
Регулировать скважность S = T / t n можно либо изменением длительности импульса t n при T =const, либо изменением периода Т при t n =const. Рассмотрим спектры сигналов при этом.
T =const, t n =var. Частота первой гармоники f 1 =1/ T = const и f = f 1 = const. Первый нуль N = T / t n и по мере укорочения импульса t n смещается в область гармоник с большими номерами. При t n 0 N , спектр получается дискретным и f = f 1 , бесконечно широкий и с бесконечно малыми амплитудами гармоник.
t n =const, T =var. Будем увеличивать период Т , тогда частота первой гармоники f 1 и расстояние между спектральными линиями f будут уменьшаться. Так как f = f 1 =1/Т , то спектральные линии будут смещаться в область более низких частот и «плотность» спектра возрастет. Если Т , то сигнал из периодического становится непериодическим (одиночный импульс). В этом случае f 1 = f 0, т.е. спектр из дискретного превращается в непрерывный, состоящий из бесконечно большого числа спектральных линий, находящихся на бесконечно малых расстояниях друг от друга.
Отсюда следует правило: периодические сигналы порождают дискретные (линейчатые) спектры, а непериодические – сплошные (непрерывные).
При переходе от дискретного спектра к непрерывному ряд Фурье заменяется интегралом Фурье. Наиболее просто эта замена выполняется, если использовать запись ряда Фурье в комплексной форме (16) и (17). Интеграл Фурье для непрерывного спектра записывается
, (30)
где
(31)
Функция F (j ) называется спектральной функцией или спектральной плотностью , которая зависит от частоты. Формулы (30) и (31) называют в совокупности односторонним преобразованием Фурье , которое является частным случаем более общего преобразования Лапласа и получается заменой в преобразовании Лапласа комплексной переменной р на j .
Спектральную
функцию можно представить как огибающую
коэффициентов ряда Фурье, т.е. как предел
линейчатого спектра периодической
функции при Т
.
Функция F
(j
)
может быть действительной или комплексной.
Считая в общем случае
,
мы получаем две частотные характеристики:
-амплитудный
спектр
, т.е.
зависимость амплитуды спектральных
составляющих от частоты, и
(
)
– фазовый
спектр
, т.е.
закон изменения фазы спектральных
составляющих сигнала от частоты. Можно
показать, что амплитудный
спектр – всегда четная, а фазовый спектр
– всегда нечетная функция
.
Спектральную функцию для многих
непериодических сигналов (одиночных
импульсов различной формы) наиболее
легко и просто находить с помощью таблиц
оригиналов и изображений в преобразовании
Лапласа, которые приводятся в учебной
и справочной литературе. После нахождения
изображения по Лапласу F
(p
)
для заданной непериодической функции
f
(t
)
,
спектральная функция находится
(32)
Итак,
согласно (30) непериодическая функция
f
(t
)
представляется совокупностью бесконечно
большого числа гармоник с бесконечно
малыми амплитудами
во всем диапазоне частот от -
до +,
т.е. представление f
(t
)
в виде интеграла Фурье подразумевает
суммирование незатухающих гармонических
колебаний бесконечного сплошного
спектра частот.
описание лабораторной установки
Работа выполняется на блоке «Синтезатор сигнала», функциональная схема которого приведена на рис. 16.
Блок содержит генераторов Г1-Г6 шести первых гармоник сигнала. Частота первой гармоники равна 10 кГц. Гармонический сигнал с выхода n-го генератора через фазовращатель Ф n и аттенюатор А n поступает на сумматор. Фазовращателями задают начальные фазы n гармоник, а аттенюаторами – их амплитуды А n .
На выходе сумматора в общем случае получается сумма шести гармоник сигнала
.
С выхода сумматора сигнал подается на вход Y осциллографа. Для его внешней синхронизации используется специальный импульсный сигнал, подаваемый с гнезда «Синхр.» на вход Х осциллографа. Для установки и контроля амплитуд гармоник предусмотрена возможность отключения любой из гармоник. Включив только генератор n-ой гармоники, можно установить ее амплитуду аттенюатором А n и оценить ее значения с помощью осциллографа. Каждый фазовращатель с помощью переключателя позволяет установить требуемое дискретное значение начальной фазы гармоники, либо отключить генератор.
Классификация сигналов и их параметры.
Электрические сигналы представляют собой электрические процессы, используемые для передачи или хранения информации.
Сигналы можно разделить на два больших класса: детерминированные и случайные. Детерминированными называются сигналы, мгновенные значения которых в любой момент времени можно предсказать с вероятностью, равной единице и которые задаются в виде некоторой определенной функции времени. Приведем несколько характерных примеров: гармонический сигнал с известной амплитудой A и периодом T (рис. 1.1 а ); последовательность прямоугольных импульсов с известным периодом следования T , длительностью t и и амплитудой A (рис. 1.1 б ); последовательность импульсов произвольной формы с известнымидлительностью t и, амплитудой A и периодом T (рис. 1.1 в ). Детерминированные сигналы не содержат никакой информации.
Случайные сигналы представляют собой хаотические функции времени, значения которых заранее неизвестны и не могут быть предсказаны с вероятностью, равной единице (одиночный импульс с длительностью t и и амплитудой A (рис. 1.1 г ) речь, музыка в выражении электрических величин). К случайным сигналам относятся также шумы.
Детерминированные сигналы, в свою очередь, подразделяются на периодические, для которых выполняется условие S (t )=S (t+kT ), где T – период, k -любое целое число, а под S (t ) понимается изменяющиеся со временем ток, напряжение или заряд (рис. 1.1 а, б, в ).
Очевидно, что к непериодическим относится любой детерминированный сигнал, для которого выполняется условие S (t )¹S (t+kT ).
Простейшим периодическим сигналом является гармонический сигнал вида 
.
Любой сложный периодический сигнал можно разложить на гармонические составляющие. Ниже такое разложение будет проведено для нескольких конкретных видов сигналов.
Гармонический сигнал высокой частоты, в котором путем модуляции заложена информация, называется радиосигналом (рис. 1.1 д ).
Периодические сигналы.
Любой сложный периодический сигнал S
(t
)=S
(t+kT
) (рис.1.2), заданный на интервале значений t
от –¥ до +¥, может быть представлен в виде суммы элементарных гармонических сигналов. Это представление осуществляется в виде ряда Фурье, если только заданная периодическая функция удовлетворяет условиям Дирихле:
1. На любом конечном интервале времени функция S (t ) должна быть непрерывна или иметь конечное число разрывов первого рода.
2. В пределах одного периода функция должна иметь конечное число максимумов и минимумов.
Обычно все реальные радиотехнические сигналы удовлетворяют этим условиям. В тригонометрической форме ряд Фурье имеет вид (1.1)
где постоянная составляющая равна 
(1.2)
а коэффициенты a n ,
и b n
при косинусоидальных и синусоидальных членах разложения определяются выражениями 
(1.3)
Амплитуда (модуль) и фаза (аргумент) n-ой
гармоники выражаются через коэффициенты a n ,
и b n
следующим образом 
(1.4)
При использовании комплексной формы записи выражение для сигнала S(t) принимает вид 
. Здесь коэффициенты 
, называемые комплексными амплитудами, равны 
и связаны с величинами а n и b n формулами: при n>0, и при n<0. С учётом обозначений 
.
Спектр периодической функции состоит из отдельных линий, соответствующих дискретным частотам 0, w, 2w, 3w …, т. е. имеет линейчатый или дискретный характер (рис.1.3). Использование рядов Фурье в сочетании с принципом суперпозици является мощным средством анализа влияния линейных систем на прохождение через них различного вида периодических сигналов.
При разложении периодической функции в ряд Фурье, следует учитывать симметрию самой функции, т. к. это позволяет упростить расчеты. В зависимости от вида симметрии представленные рядом Фурье функции могут:
1. 
Не иметь постоянной составляющей если площадь фигуры для положительного полупериода равна площади фигуры для отрицательного полупериода.
2. Не иметь четных гармоник и постоянной составляющей, если значения функции повторяются через половину периода с обратным знаком.
Спектральный состав последовательности прямоугольных импульсов при различном периоде их скважности.
Периодическая последовательность прямоугольных импульсов изображена на рис. 1.4. Постоянная составляющая ряда Фурье определяется из выражения и для данного случая равна 
.
Амплитуда cos-составлящей а n
равна
, а амплитуда sin-составляющей b n
равна 
.
Амплитуда n
-ой гармоники 
