1. Całki niewłaściwe o granicach nieskończonych
Przypomnijmy definicję całki jako granicy sum całkowitych: 
Definicja zakłada, że przedział całkowania jest skończony, a funkcja f(x) jest w nim ciągła. Naruszenie tych założeń prowadzi do całek niewłaściwych.
Definicja. Jeśli całka dąży do skończonej granicy, gdy rośnie w nieskończoność "B", wówczas granicę tę nazywamy całką niewłaściwą z nieskończoną górną granicą funkcji f (x) i oznaczamy symbolem 
W tym przypadku mówimy, że całka niewłaściwa istnieje lub jest zbieżna.
Jeśli określona granica nie istnieje lub istnieje, ale jest nieskończona, wówczas całkę mówimy, że nie istnieje lub jest rozbieżna.
Całkę niewłaściwą z nieskończoną dolną granicą definiuje się podobnie:

Całkę niewłaściwą z dwiema nieskończonymi granicami podaje wzór:

gdzie c jest dowolnym stałym punktem na osi Wół.
Zatem całki niewłaściwe mogą mieć nieskończoną dolną granicę, nieskończoną górną granicę, a także dwie nieskończone granice.
Oznaki konwergencji. Zbieżność bezwzględna i warunkowa
Całka istnieje tylko wtedy, gdy istnieje każda z całek: oraz .
Przykład. Zbadaj zbieżność całki
Zakładając c = 0, otrzymujemy:

te. całka jest zbieżna.
Czasami nie ma potrzeby obliczania całki niewłaściwej, wystarczy po prostu wiedzieć, czy jest ona zbieżna, czy rozbieżna, porównując ją z inną całką.
Twierdzenie porównawcze dla całek niewłaściwych.
Niech funkcja f(x) w przedziale ma kilka (skończoną liczbę) punktów nieciągłości pierwszego rodzaju, tę „przeszkodę” można łatwo wyeliminować dzieląc odcinek z punktami nieciągłości na kilka odcinków, obliczając całki oznaczone na każdym odcinku i dodanie wyników.
Rozważmy całkę oznaczoną funkcji, która jest nieograniczona w momencie dochodzenia do jednego z końców odcinka, na przykład: ![]() .
.
(W takich przypadkach zwykle mówią: „Funkcja ma nieskończoną nieciągłość na prawym końcu przedziału całkowania”.)
Oczywiste jest, że zwykła definicja całki traci tutaj swoje znaczenie.
Definicja. Całka niewłaściwa funkcji f(x), ciągła dla £ x< b и неограниченной при x ® b - 0, называется предел:

Całkę niewłaściwą funkcji, która ma nieskończoną nieciągłość na lewym końcu odcinka, definiuje się podobnie:

W konsekwencji w odcinku [-1, 0] całka jest rozbieżna.

Oznacza to, że całka jest również rozbieżna w przekroju.
Zatem całka ta jest rozbieżna na całym przedziale [-1, 1]. Zauważmy, że gdybyśmy zaczęli obliczać tę całkę, nie zwracając uwagi na nieciągłość całki w punkcie x = 0, otrzymalibyśmy błędny wynik. Naprawdę,
 , co jest niemożliwe.
, co jest niemożliwe.
Aby więc zbadać całkę nieciągłą funkcji nieciągłej, konieczne jest „podzielenie” jej na kilka całek i zbadanie ich.
Jak wiadomo, znalezienie całki może być dość trudnym zadaniem. Wielkim rozczarowaniem byłoby rozpoczęcie obliczania całki niewłaściwej i stwierdzenie na końcu ścieżki, że jest ona rozbieżna. Dlatego interesujące są metody, które pozwalają bez poważnych obliczeń opartych na jednym rodzaju funkcji wyciągnąć wniosek o zbieżności lub rozbieżności całki niewłaściwej. Pierwsze i drugie twierdzenie porównawcze, które zostaną omówione poniżej, bardzo pomagają w badaniu całek niewłaściwych pod kątem zbieżności.
Niech f(x)?0. Następnie funkcje
rosną monotonicznie w zmiennych t lub -g (ponieważ bierzemy g>0, -g dąży do zera od lewej strony). Jeśli wraz ze wzrostem argumentów funkcje F 1 (t) i F 2 (-d) pozostaną ograniczone z góry, oznacza to, że odpowiednie całki niewłaściwe są zbieżne. Jest to podstawa pierwszego twierdzenia porównawczego dla całek funkcji nieujemnych.
Niech funkcje f(x) i g(x) przy x?a spełniają następujące warunki:
- 1) 0?f(x)?g(x);
- 2) Funkcje f(x) i g(x) są ciągłe.
Wtedy ze zbieżności całki wynika zbieżność całki, a z rozbieżności całki wynika rozbieżność
Ponieważ 0?f(x)?g(x) i funkcje są ciągłe, zatem
Pod warunkiem całka jest zbieżna, tj. ma skończoną wartość. Zatem całka również jest zbieżna.
Niech teraz całka będzie rozbieżna. Załóżmy, że całka jest zbieżna, ale wtedy całka musi być zbieżna, co jest sprzeczne z warunkiem. Nasze założenie jest błędne, całka jest rozbieżna.
Twierdzenie porównawcze dla całek niewłaściwych drugiego rodzaju.
Niech dla funkcji f(x) i g(x) na przedziale , zwiększaj bez ograniczeń dla x>+0. Dla x>+0 zachodzi nierówność:<. Несобственный интеграл есть эталонный интеграл 2-го рода, который при p=<1 сходится; следовательно, по 1-й теореме сравнения для несобственных интегралов 2-го рода интеграл сходится также.
Twierdzenie porównawcze dla całek niewłaściwych pierwszego rodzaju.
Niech funkcje f(x) i g(x) będą na przedziale , a segment całkowania będzie skończony, czyli ograniczony liczbami, a nie nieskończonością. Niektóre zadania powodują konieczność rezygnacji z tych ograniczeń. Tak wyglądają całki niewłaściwe.
Znaczenie geometryczne całki niewłaściwej Okazuje się to po prostu proste. W przypadku gdy wykres funkcji y = F(X) znajduje się nad osią Wół, całka oznaczona wyraża pole zakrzywiony trapez, ograniczony krzywą y = F(X) , oś x i współrzędne X = A , X = B. Z kolei całka niewłaściwa wyraża pole nieograniczonego (nieskończonego) trapezu krzywoliniowego zamkniętego między liniami y = F(X) (na zdjęciu poniżej - kolor czerwony), X = A i oś odciętych.

Całki niewłaściwe definiuje się podobnie dla innych przedziałów nieskończonych:
Pole nieskończonego zakrzywionego trapezu może być liczbą skończoną, w tym przypadku całkę niewłaściwą nazywa się zbieżną. Pole może być również nieskończone i w tym przypadku całkę niewłaściwą nazywamy rozbieżną.
Używanie granicy całki zamiast samej całki niewłaściwej. Aby obliczyć całkę niewłaściwą, należy skorzystać z granicy Całka oznaczona. Jeżeli ta granica istnieje i jest skończona (nie równa się nieskończoności), to całkę niewłaściwą nazywamy zbieżną, a w przeciwnym razie - rozbieżną. To, do czego zmienna zmierza pod znakiem granicy, zależy od tego, czy mamy do czynienia z całką niewłaściwą pierwszego rodzaju, czy drugiego rodzaju. Przekonajmy się o tym teraz.
Całki niewłaściwe pierwszego rodzaju - o granicach nieskończonych i ich zbieżności
Całki niewłaściwe z nieskończoną górną granicą
Zatem zapisanie całki niewłaściwej różni się od zwykłej całki oznaczonej tym, że górna granica całkowania jest nieskończona.
Definicja. Całka niewłaściwa z nieskończoną górną granicą całkowania funkcji ciągłej F(X) w przerwie od A Do ∞ nazywa się granicę całki tej funkcji z górną granicą całkowania B i dolna granica całkowania A pod warunkiem, że górna granica integracji będzie rosła bez ograniczeń, tj.
![]() .
.
Jeśli ta granica istnieje i jest równa jakiejś liczbie, a nie nieskończoności, to Całkę niewłaściwą nazywamy zbieżną, a za jego wartość przyjmuje się liczbę, do której równa jest granica. W przeciwnym razie Całkę niewłaściwą nazywamy rozbieżną i nie przypisuje się mu żadnego znaczenia.
Przykład 1. Oblicz całkę niewłaściwą(jeśli jest zbieżny).
Rozwiązanie. Na podstawie definicji całki niewłaściwej znajdujemy

Ponieważ granica istnieje i jest równa 1, to to Całka niewłaściwa jest zbieżna i jest równe 1.
W poniższym przykładzie całka jest prawie taka sama jak w przykładzie 1, tylko stopień x to nie dwa, ale litera alfa, a zadaniem jest zbadanie całki niewłaściwej pod kątem zbieżności. Oznacza to, że pozostaje pytanie: przy jakich wartościach alfa zbiega się ta całka niewłaściwa, a przy jakich wartościach się rozbiega?
Przykład 2. Zbadaj całkę niewłaściwą pod kątem zbieżności(dolna granica całkowania jest większa od zera).
Rozwiązanie. Załóżmy więc najpierw, że

W otrzymanym wyrażeniu przechodzimy do granicy w:
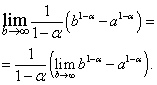
Łatwo zauważyć, że granica po prawej stronie istnieje i jest równa zeru, gdy , czyli , i nie istnieje, gdy , czyli .
W pierwszym przypadku, czyli kiedy . Jeśli, to  i nie istnieje.
i nie istnieje.
Wniosek z naszego badania jest następujący: to Całka niewłaściwa jest zbieżna w i różni się Na .
Zastosowanie wzoru Newtona-Leibniza do rodzaju badanej całki niewłaściwej ![]() , można wyprowadzić następującą formułę, która jest do niej bardzo podobna:
, można wyprowadzić następującą formułę, która jest do niej bardzo podobna:
 .
.
Jest to uogólniony wzór Newtona-Leibniza.
Przykład 3. Oblicz całkę niewłaściwą(jeśli jest zbieżny).
Granica tej całki istnieje:
![]()
Całka druga, tworząca sumę wyrażającą całkę pierwotną:

Granica tej całki również istnieje:
![]() .
.
Znajdujemy sumę dwóch całek, która jest jednocześnie wartością pierwotnej całki niewłaściwej z dwiema nieskończonymi granicami:
Całki niewłaściwe drugiego rodzaju - z funkcji nieograniczonych i ich zbieżności
Niech funkcja F(X) podane w segmencie od A Do B i jest na nim nieograniczony. Załóżmy, że funkcja zmierza w tym punkcie do nieskończoności B , podczas gdy we wszystkich pozostałych punktach odcinka jest ciągły.
Definicja. Całka niewłaściwa funkcji F(X) na odcinku od A Do B nazywa się granicę całki tej funkcji z górną granicą całkowania C , jeśli podczas wysiłku C Do B funkcja rośnie bez ograniczeń i w punkcie X = B funkcja nie zdefiniowana, tj.
![]() .
.
Jeżeli ta granica istnieje, to całkę niewłaściwą drugiego rodzaju nazywamy zbieżną, w przeciwnym razie nazywamy ją rozbieżną.
Korzystając ze wzoru Newtona-Leibniza, wyprowadzamy.
Jeżeli całka ma nieciągłość drugiego rodzaju na (skończonym) przedziale całkowania, to mówimy o całce niewłaściwej drugiego rodzaju.
10.2.1 Definicja i podstawowe właściwości
Oznaczmy przedział całkowania przez $\left[ a, \, b \right ]$, poniżej zakładamy, że obie te liczby są skończone. Jeżeli jest tylko 1 nieciągłość, to może ona znajdować się albo w punkcie $a$, albo w punkcie $b$, albo wewnątrz przedziału $(a,\,b)$. Rozważmy najpierw przypadek, gdy w punkcie $a$ występuje nieciągłość drugiego rodzaju, a w pozostałych punktach funkcja całki jest ciągła. Mówimy więc o całce
\begin(równanie) I=\int _a^b f(x)\,dx, (22) \label(intr2) \end(równanie)
i $f(x) \rightarrow \infty $ kiedy $x \rightarrow a+0$. Tak jak poprzednio, pierwszą rzeczą, którą należy zrobić, jest nadanie znaczenia temu wyrażeniu. Aby to zrobić, rozważ całkę
\[ I(\epsilon)=\int _(a+\epsilon)^b f(x)\,dx. \]
Definicja. Niech będzie skończona granica
\[ A=\lim _(\epsilon \rightarrow +0)I(\epsilon)=\lim _(\epsilon \rightarrow +0)\int _(a+\epsilon)^b f(x)\,dx. \]
Wtedy mówimy, że całka niewłaściwa drugiego rodzaju (22) jest zbieżna i przypisuje się jej wartość $A$, a sama funkcja $f(x)$ jest całkowalna na przedziale $\left[ a, \ , b\right]$.
Rozważ całkę
\[ I=\int ^1_0\frac(dx)(\sqrt(x)). \]
Funkcja całkowa $1/\sqrt(x)$ w $x \rightarrow +0$ ma nieskończoną granicę, więc w punkcie $x=0$ ma nieciągłość drugiego rodzaju. Połóżmy
\[ I(\epsilon)=\int ^1_(\epsilon )\frac(dx)(\sqrt(x))\,. \]
W tym przypadku znana jest funkcja pierwotna,
\[ I(\epsilon)=\int ^1_(\epsilon )\frac(dx)(\sqrt(x))=2\sqrt(x)|^1_(\epsilon )=2(1-\sqrt( \epsilon ))\rightarrow 2\]
w $\epsilon \rightarrow +0$. Zatem całka pierwotna jest zbieżną całką niewłaściwą drugiego rodzaju i jest równa 2.
Rozważmy opcję, gdy w funkcji całkowej występuje nieciągłość drugiego rodzaju w górnej granicy przedziału całkowania. Przypadek ten można sprowadzić do poprzedniego dokonując zmiany zmiennej $x=-t$, a następnie przestawiając granice całkowania.
Rozważmy opcję, gdy funkcja całkowa ma nieciągłość drugiego rodzaju wewnątrz przedziału całkowania, w punkcie $c \in (a,\,b)$. W tym przypadku całka pierwotna
\begin(równanie) I=\int _a^bf(x)\,dx (23) \label(intr3) \end(równanie)
prezentowane jako suma
\[ I=I_1+I_2, \quad I_1=\int _a^cf(x)\,dx +\int _c^df(x)\,dx. \]
Definicja. Jeżeli obie całki $I_1, \, I_2$ są zbieżne, to całkę niewłaściwą (23) nazywamy zbieżną i przypisuje się jej wartość równą sumie całek $I_1, \, I_2$, funkcji $f(x)$ nazywa się całkowalnym w przedziale $\left [a, \, b\right]$. Jeżeli chociaż jedna z całek $I_1,\, I_2$ jest rozbieżna, całkę niewłaściwą (23) nazywamy rozbieżną.
Zbieżne całki niewłaściwe drugiego rodzaju mają wszystkie standardowe właściwości zwykłych całek oznaczonych.
1. Jeśli $f(x)$, $g(x)$ są całkowalne na przedziale $\left[ a, \,b \right ]$, to ich suma $f(x)+g(x)$ wynosi również całkowalne w tym przedziale, i \[ \int _a^(b)\left(f(x)+g(x)\right)dx=\int _a^(b)f(x)dx+\int _a^( b)g (x)dx. \] 2. Jeśli $f(x)$ jest całkowalne na przedziale $\left[ a, \, b \right ]$, to dla dowolnej stałej $C$ funkcja $C\cdot f(x)$ jest również całkowalne na tym przedziale i \[ \int _a^(b)C\cdot f(x)dx=C \cdot \int _a^(b)f(x)dx. \] 3. Jeśli $f(x)$ jest całkowalne na przedziale $\left[ a, \, b \right ]$ i na tym przedziale $f(x)>0$, to \[ \int _a^ (b ) f(x)dx\,>\,0. \] 4. Jeśli $f(x)$ jest całkowalne na przedziale $\left[ a, \, b \right ]$, to dla dowolnego $c\in (a, \,b)$ całki \[ \ int _a^ (c) f(x)dx, \quad \int _c^(b) f(x)dx \] również zbiegają się, a \[ \int _a^(b)f(x)dx=\int _a ^(c ) f(x)dx+\int _c^(b) f(x)dx \] (addytywność całki po przedziale).
Rozważ całkę \begin(równanie) I=\int _0^(1)\frac(1)(x^k)\,dx. (24) \label(mod2) \end(równanie) Jeśli $k>0$, całka dąży do $\infty$ jako $x \rightarrow +0$, więc całka jest niewłaściwa drugiego rodzaju. Przedstawmy funkcję \[ I(\epsilon)=\int _(\epsilon)^(1)\frac(1)(x^k)\,dx. \] W tym przypadku znana jest funkcja pierwotna, czyli tzw \[ I(\epsilon)=\int _(\epsilon)^(1)\frac(1)(x^k)\,dx\,=\frac(x^(1-k))(1-k )|_(\epsilon)^1= \frac(1)(1-k)-\frac(\epsilon ^(1-k))(1-k). \] za $k \neq 1$, \[ I(\epsilon)=\int _(\epsilon)^(1)\frac(1)(x)\,dx\,=lnx|_(\epsilon)^1= -ln \epsilon. \] dla $k = 1$. Biorąc pod uwagę zachowanie przy $\epsilon \rightarrow +0$, dochodzimy do wniosku, że całka (20) jest zbieżna przy $k
10.2.2 Testy na zbieżność całek niewłaściwych II rodzaju
Twierdzenie (pierwszy znak porównania). Niech $f(x)$, $g(x)$ będą ciągłe dla $x\in (a,\,b)$ i $0 1. Jeśli całka \[ \int _a^(b)g(x) dx \] jest zbieżny, to całka \[ \int _a^(b)f(x)dx jest zbieżna. \] 2. Jeśli całka \[ \int _a^(b)f(x)dx \] jest rozbieżna, to całka \[ \int _a^(b)g(x)dx jest rozbieżna. \]
Twierdzenie (drugie kryterium porównania). Niech $f(x)$, $g(x)$ będą ciągłe i dodatnie dla $x\in (a,\,b)$ i niech będzie skończona granica
\[ \theta = \lim_(x \rightarrow a+0) \frac(f(x))(g(x)), \quad \theta \neq 0, \, +\infty. \]
Następnie całki
\[ \int _a^(b)f(x)dx, \quad \int _a^(b)g(x)dx \]
zbiegają się lub rozchodzą jednocześnie.
Rozważ całkę
\[ I=\int _0^(1)\frac(1)(x+\sin x)\,dx. \]
Wyrażenie całkowe to funkcja pozytywna w przedziale całkowania całka dąży do $\infty$ jako $x \rightarrow +0$, więc nasza całka jest całką niewłaściwą drugiego rodzaju. Dalej, dla $x \rightarrow +0$ mamy: jeśli $g(x)=1/x$, to
\[ \lim _(x \rightarrow +0)\frac(f(x))(g(x))=\lim _(x \rightarrow +0)\frac(x)(x+\sin x)=\ frac(1)(2) \neq 0,\, \infty \, . \]
Stosując drugie kryterium porównania dochodzimy do wniosku, że nasza całka jest zbieżna lub rozbieżna jednocześnie z całką
\[ \int _0^(+1)\frac(1)(x)\,dx . \]
Jak pokazano w poprzednim przykładzie, całka ta jest rozbieżna ($k=1$). W związku z tym całka pierwotna również jest rozbieżna.
Oblicz całkę niewłaściwą lub ustal jej zbieżność (rozbieżność).
1. \[ \int _(0)^(1)\frac(dx)(x^3-5x^2)\,. \] 2. \[ \int _(3)^(7)\frac(x\,dx)((x-5)^2)\,. \] 3. \[ \int _(0)^(1)\frac(x\,dx)(\sqrt(1-x^2))\,. \] 4. \[ \int _(0)^(1)\frac(x^3\,dx)(1-x^5)\,. \] 5. \[ \int _(-3)^(2)\frac(dx)((x+3)^2)\,. \] 6. \[ \int _(1)^(2)\frac(x^2\,dx)((x-1)\sqrt(x-1))\,. \] 7. \[ \int _(0)^(1)\frac(dx)(\sqrt(x+x^2))\,. \] 8. \[ \int _(0)^(1/4)\frac(dx)(\sqrt(x-x^2))\,. \] 9. \[ \int _(1)^(2)\frac(dx)(xlnx)\,. \] 10. \[ \int _(1)^(2)\frac(x^3\,dx)(\sqrt(4-x^2))\,. \] 11. \[ \int _(0)^(\pi /4)\frac(dx)(\sin ^4x)\,. \]