Uygulamalı derste, "Trigonometri" konusundaki ana görev türlerini tekrar edeceğiz, ayrıca artan karmaşıklıktaki sorunları analiz edeceğiz ve çeşitli trigonometrik eşitsizlikleri ve sistemlerini çözme örneklerini ele alacağız.
Bu ders, B5, B7, C1 ve C3 görev türlerinden birine hazırlanmanıza yardımcı olacaktır.
Trigonometri konusunda incelediğimiz ana görev türlerini tekrarlayarak başlayalım ve standart olmayan birkaç görevi çözelim.
Görev 1. Açıları radyan ve dereceye dönüştürün: a) ; B) .
a) Dereceleri radyana dönüştürmek için formülü kullanın
Verilen değeri yerine koyun.
b) Radyanları dereceye dönüştürmek için formülü uygulayın
Değiştirme işlemini yapalım 
.
Cevap. A) ; B) .
görev #2. Hesapla: a) ; B) .
a) Açı tablonun çok ötesinde olduğu için sinüsün periyodunu çıkararak açıyı azaltırız. Çünkü açı radyan cinsinden verilirse, periyot olarak kabul edilir.
b) Bu durumda durum benzerdir. Açı derece olarak belirtildiğinden, teğetin periyodunu olarak kabul edeceğiz.
Ortaya çıkan açı, periyoddan daha küçük olmasına rağmen daha büyüktür, yani artık tablonun ana değil, uzatılmış kısmına atıfta bulunur. Genişletilmiş bir trigofonksiyon değerleri tablosunu ezberleyerek hafızamızı bir kez daha eğitmemek için teğet periyodu tekrar çıkarırız:
Teğet fonksiyonunun tuhaflığından faydalandık.
Cevap. a) 1; B) .
Görev #3. Hesaplamak 
, Eğer .
Kesrin payını ve paydasını ile bölerek tüm ifadeyi teğetlere getiriyoruz. Aynı zamanda bundan korkamayız çünkü bu durumda teğetin değeri olmayacaktır.
Görev #4. Ifadeyi basitleştir.
Belirtilen ifadeler, dönüştürme formülleri kullanılarak dönüştürülür. Sadece alışılmadık bir şekilde derece kullanılarak yazılmışlar. İlk ifade genellikle bir sayıdır. Sırayla tüm trigofonksiyonları basitleştirin:
Çünkü , sonra işlev bir ortak işleve dönüşür, yani kotanjanta ve açı, orijinal teğetin işaretinin negatif olduğu ikinci çeyreğe düşer.
Önceki ifadeyle aynı nedenlerle, işlev bir ortak işleve dönüşür, yani. kotanjanta ve açı, ilk teğetin pozitif işaretli olduğu ilk çeyreğe düşer.
Her şeyi basitleştirilmiş bir ifadeyle değiştirmek:
Görev #5. Ifadeyi basitleştir.
Çift açının tanjantını ilgili formüle göre yazalım ve ifadeyi sadeleştirelim:
Son kimlik, kosinüs için evrensel değiştirme formüllerinden biridir.
görev #6. Hesaplamak .
Esas olan standart bir hata yapmamak ve ifade eşittir şeklinde bir cevap vermemektir. Yanında iki şeklinde bir çarpan varken ark teğetinin ana özelliğini kullanmak mümkün değildir. Bundan kurtulmak için, ifadeyi sıradan bir argüman olarak ele alırken, bir çift açının teğet formülüne göre yazıyoruz.
Artık ark teğetinin ana özelliğini uygulamak zaten mümkün, sayısal sonucu üzerinde herhangi bir kısıtlama olmadığını unutmayın.
Görev #7. Denklemi çözün.
Sıfıra eşit olan bir kesirli denklemi çözerken, her zaman payın sıfır olduğu ve paydanın olmadığı belirtilir, çünkü sıfıra bölemezsiniz.
İlk denklem, trigonometrik bir daire kullanılarak çözülen en basit denklemin özel bir halidir. Bu çözümü kendiniz düşünün. İkinci eşitsizlik, teğetin kökleri için genel formül kullanılarak en basit denklem olarak çözülür, ancak yalnızca işaret eşit değildir.
Gördüğümüz gibi, bir kök ailesi, denklemi sağlamayan tam olarak aynı kök ailesini dışlar. Onlar. kökleri yoktur.
Cevap. Kök yok.
görev #8. Denklemi çözün.
Derhal ortak faktörü çıkarabileceğinizi ve yapabileceğinizi unutmayın:
Denklem, birkaç faktörün çarpımı sıfıra eşit olduğunda standart formlardan birine indirgenmiştir. Bu durumda birinin sıfıra, diğerinin veya üçüncünün eşit olduğunu zaten biliyoruz. Bunu bir denklem seti olarak yazıyoruz:
İlk iki denklem en basitlerinin özel durumlarıdır, benzer denklemlerle zaten birçok kez karşılaştık, bu yüzden hemen çözümlerini göstereceğiz. Çift açılı sinüs formülünü kullanarak üçüncü denklemi bir fonksiyona indirgeriz.
Son denklemi ayrı ayrı çözelim:
Bu denklemin kökleri yoktur, çünkü sinüsün değeri ötesine geçemez 
.
Bu nedenle, yalnızca ilk iki kök ailesi çözümdür, bunlar bir trigonometrik daire üzerinde gösterilmesi kolay olan bir ailede birleştirilebilirler:
 |
Bu, tüm yarılardan oluşan bir ailedir, yani.
Trigonometrik eşitsizlikleri çözmeye geçelim. İlk olarak, genel çözüm formüllerini kullanmadan, ancak bir trigonometrik daire yardımıyla bir örneği çözme yaklaşımını analiz edelim.
görev #9. Eşitsizliği çöz.
Sinüs değerine karşılık gelen trigonometrik daire üzerine bir yardımcı çizgi çizin ve eşitsizliği sağlayan açıların aralığını gösterin.
 |
Ortaya çıkan açı aralığının tam olarak nasıl belirleneceğini anlamak çok önemlidir, örn. başlangıcı ve sonu nedir. Boşluğun başlangıcı, saat yönünün tersine hareket edersek boşluğun en başında gireceğimiz noktaya karşılık gelen açı olacaktır. Bizim durumumuzda soldaki nokta burası çünkü saat yönünün tersine hareket ederek doğru noktayı geçerek tam tersine gerekli açı aralığından çıkıyoruz. Bu nedenle doğru nokta, boşluğun sonuna karşılık gelecektir.
Şimdi eşitsizliğin çözüm boşluğumuzun başlangıç ve bitiş açılarının değerlerini anlamamız gerekiyor. Tipik bir hata, sağ noktanın soldaki açıya karşılık geldiğini hemen belirtmek ve cevabı vermektir. Bu doğru değil! Lütfen dikkat edin, çemberin üst kısmına karşılık gelen aralığı az önce belirttik, alt kısımla ilgilenmemize rağmen, başka bir deyişle, ihtiyacımız olan çözüm aralığının başlangıcını ve sonunu karıştırdık.
Aralığın sağ noktanın köşesinden başlayıp sol noktanın köşesinde bitmesi için ilk belirtilen açının ikinciden küçük olması gerekir. Bunu yapmak için, doğru noktanın açısını negatif referans yönünde ölçmemiz gerekecek, yani. saat yönünde ve eşit olacaktır. Daha sonra ondan pozitif saat yönünde başlayarak sol noktadan sonra sağdaki noktaya gelip açının değerini alacağız. Şimdi açılar aralığının başlangıcı, sonundan küçüktür ve periyodu hesaba katmadan çözüm aralığını yazabiliriz:
Bu tür aralıkların, herhangi bir tam sayı döndürmeden sonra sonsuz sayıda tekrarlanacağını göz önünde bulundurarak, sinüs periyodunu dikkate alarak genel çözümü elde ederiz:
Eşitsizlik katı olduğu için yuvarlak parantezler içine alıyoruz ve çemberin üzerinde aralığın sonlarına denk gelen noktaları deliyoruz.
Cevabınızı derste verdiğimiz genel çözüm formülü ile karşılaştırın.
Cevap. 
.
Bu yöntem, en basit trigonal eşitsizliklerin genel çözüm formüllerinin nereden geldiğini anlamak için iyidir. Ayrıca tüm bu hantal formülleri öğrenemeyecek kadar tembel olanlar için faydalıdır. Bununla birlikte, yöntemin kendisi de kolay değildir, çözüme hangi yaklaşımın sizin için en uygun olduğunu seçin.
Trigonometrik eşitsizlikleri çözmek için, birim çember kullanılarak gösterilen yönteme benzer şekilde, yardımcı doğrunun üzerine kurulduğu fonksiyon grafiklerini de kullanabilirsiniz. Eğer ilgileniyorsanız, çözüme yönelik bu yaklaşımı kendiniz anlamaya çalışın. Aşağıda, en basit trigonometrik eşitsizlikleri çözmek için genel formülleri kullanacağız.
Görev #10. Eşitsizliği çöz.
Eşitsizliğin kesin olmadığını dikkate alarak genel çözüm formülünü kullanıyoruz:
Bizim durumumuzda:
Cevap. 
Görev #11. Eşitsizliği çöz.
Karşılık gelen kesin eşitsizlik için genel çözüm formülünü kullanırız:
Cevap. 
.
Görev #12. Eşitsizlikleri çözün: a) ; B) .
Bu eşitsizliklerde genel çözümler için formüller kullanmakta acele edilmemeli veya trigonometrik daire, sadece sinüs ve kosinüs aralığını hatırlayın.
a) Çünkü 
, o zaman eşitsizlik anlamsızdır. Bu nedenle, çözümler yoktur.
b) Çünkü benzer şekilde, herhangi bir bağımsız değişkenin sinüsü her zaman koşulda belirtilen eşitsizliği karşılar. Bu nedenle eşitsizlik, argümanın tüm gerçek değerleri tarafından karşılanır.
Cevap. a) çözüm yok; B) .
Görev 13. eşitsizliği çöz 
.
TRİGONOMETRİK EŞİTSİZLİKLERİ ÇÖZME YÖNTEMLERİ
alaka. Tarihsel olarak, trigonometrik denklemler ve eşitsizliklere okul müfredatında özel bir yer verilmiştir. Trigonometri en önemli bölümlerden biridir diyebiliriz. okul kursu ve genel olarak tüm matematik.
Trigonometrik denklemler ve eşitsizlikler, hem içerik olarak hem de lise matematik dersinde merkezi yerlerden birini işgal eder. Eğitim materyali ve çalışmaları sırasında oluşturulabilen ve oluşturulması gereken ve teorik ve uygulamalı nitelikteki çok sayıda sorunun çözümüne uygulanan eğitimsel ve bilişsel aktivite yöntemleriyle.
Trigonometrik denklemlerin ve eşitsizliklerin çözümü, öğrencilerin trigonometrideki tüm eğitim materyalleriyle ilgili bilgilerini (örneğin, trigonometrik fonksiyonların özellikleri, trigonometrik ifadeleri dönüştürme yöntemleri vb.) Sistematize etmek için ön koşulları oluşturur ve etkili bağlantılar kurmayı mümkün kılar. cebirde çalışılan materyal (denklemler, denklemlerin eşdeğerliği, eşitsizlikler, cebirsel ifadelerin özdeş dönüşümleri, vb.).
Başka bir deyişle, trigonometrik denklemleri ve eşitsizlikleri çözme yöntemlerinin ele alınması, bu becerilerin bir tür yeni içeriğe aktarılmasını içerir.
Teorinin önemi ve sayısız uygulaması, seçilen konunun alaka düzeyinin kanıtıdır. Bu da, ders çalışmasının amaçlarını, hedeflerini ve araştırma konusunu belirlemenizi sağlar.
Bu çalışmanın amacı: mevcut trigonometrik eşitsizlik türlerini, bunların çözümü için temel ve özel yöntemleri genelleştirin, okul çocukları tarafından trigonometrik eşitsizlikleri çözmek için bir dizi görev seçin.
Araştırma hedefleri:
1. Araştırma konusuyla ilgili mevcut literatürün analizine dayanarak, materyali sistematik hale getirin.
2. "Trigonometrik eşitsizlikler" konusunu pekiştirmek için gerekli bir dizi görev verin.
çalışmanın amacı okul matematik dersindeki trigonometrik eşitsizliklerdir.
Çalışma konusu: trigonometrik eşitsizlik türleri ve çözüm yöntemleri.
teorik önemi materyali düzenlemektir.
pratik önemi: problem çözmede teorik bilginin uygulanması; trigonometrik eşitsizlikleri çözmek için sık karşılaşılan başlıca yöntemlerin analizi.
Araştırma Yöntemleri : bilimsel literatürün analizi, edinilen bilginin sentezi ve genelleştirilmesi, problem çözmenin analizi, eşitsizlikleri çözmek için en uygun yöntemlerin araştırılması.
§1. Trigonometrik eşitsizlik türleri ve bunların çözümü için temel yöntemler
1.1. En basit trigonometrik eşitsizlikler
Bir veya > işaretiyle birbirine bağlanan iki trigonometrik ifadeye trigonometrik eşitsizlikler denir.
Bir trigonometrik eşitsizliği çözmek, altında eşitsizliğin karşılandığı, eşitsizliğe dahil olan bilinmeyenlerin bir dizi değerini bulmak anlamına gelir.
Trigonometrik eşitsizliklerin ana kısmı, en basit olanları çözmeye indirgenerek çözülür:
Bu bir çarpanlara ayırma yöntemi olabilir, değişken değiştirme ( 
, 
vb.), olağan eşitsizliğin önce çözüldüğü ve ardından formun eşitsizliğinin çözüldüğü yer 
vb. veya başka yollar.
En basit eşitsizlikler iki şekilde çözülür: birim çember kullanılarak veya grafiksel olarak.
İzin vermekf(x
temel trigonometrik fonksiyonlardan biridir. eşitsizliği çözmek için 
çözümünü bir periyotta bulmak yeterlidir, yani uzunluğu fonksiyonun periyoduna eşit olan herhangi bir doğru parçasındaF
X
. O zaman orijinal eşitsizliğin çözümü tamamen bulunacaktır.X
, ayrıca işlevin herhangi bir tamsayı periyodu tarafından bulunan değerlerden farklı olan değerler. Bu durumda, grafik yöntemini kullanmak uygundur.
Eşitsizlikleri çözmek için bir algoritma örneği verelim. 
(
) Ve 
.
Eşitsizliği çözmek için algoritma (
).
1. Bir sayının sinüsünün tanımını formüle edinX birim çember üzerinde.
3. Y ekseninde koordinatı olan bir noktayı işaretleyin.A .
4. Bu noktadan OX eksenine paralel bir çizgi çizin ve daire ile kesiştiği noktaları işaretleyin.
5. Tüm noktalarının ordinatı şundan küçük olan bir daire yayı seçin:A .
6. Baypasın yönünü (saat yönünün tersine) belirtin ve aralığın sonlarına fonksiyonun periyodunu ekleyerek cevabı yazın.2πn
,
.
Eşitsizliği çözmek için algoritma .
1. Bir sayının tanjantının tanımını formüle edinX birim çember üzerinde.
2. Bir birim çember çizin.
3. Bir teğet çizgisi çizin ve üzerinde bir noktayı ordinat ile işaretleyinA .
4. Bu noktayı orijine bağlayın ve ortaya çıkan parçanın birim daire ile kesişme noktasını işaretleyin.
5. Tüm noktaları teğet çizgi üzerinde şu değerden küçük bir ordinata sahip olan bir daire yayı seçin:A .
6. Geçişin yönünü belirtin ve işlevin kapsamını dikkate alarak bir nokta ekleyerek cevabı yazın.pn
,
(kaydın sol tarafındaki sayı her zaman sağ tarafındaki sayıdan küçüktür).
En basit denklemlerin çözümlerinin grafiksel yorumu ve eşitsizlikleri genel bir biçimde çözmek için formüller ekte verilmiştir (Ek 1 ve 2).
örnek 1
eşitsizliği çöz 
.
Birim çember üzerine bir çizgi çizin 
, çemberi A ve B noktalarında keser.
Tüm değerlery
NM aralığında daha fazla
, AMB yayının tüm noktaları bu eşitsizliği karşılar. Tüm dönüş açılarında, büyük 
, ancak daha küçük 
,
değerinden daha büyük değerler alacaktır.
(ama birden fazla değil).
Şekil 1
Böylece eşitsizliğin çözümü, aralıktaki tüm değerler olacaktır. 
, yani 
. Bu eşitsizliğin tüm çözümlerini elde etmek için, bu aralığın sonuna eklemek yeterlidir. 
, Nerede 
, yani 
,
.
değerlerin 
Ve 
denklemin kökleri 
,
onlar. 
;
.
Cevap: 
, .
1.2. Grafik yöntem
Uygulamada, trigonometrik eşitsizlikleri çözmek için grafik bir yöntem genellikle yararlıdır. Eşitsizlik örneğinde yöntemin özünü düşünün 
:
1. Argüman karmaşıksa (farklıX ), sonra şununla değiştiririz:T .
2. Bir koordinat düzleminde inşa ediyoruztooy
fonksiyon grafikleri 
Ve 
.
3. Böyle buluyoruzgrafiklerin kesiştiği iki bitişik nokta, hangileri arasındasinüzoidalbulunandaha yüksek
dümdüz . Bu noktaların apsislerini bulun.
4. Argüman için bir çift eşitsizlik yazınT , kosinüs periyodu dikkate alındığında (T bulunan apsisler arasında olacaktır).
5. Bir ters ikame yapın (orijinal bağımsız değişkene geri dönün) ve değeri ifade edinX çift eşitsizlikten, cevabı sayısal bir aralık olarak yazıyoruz.
Örnek 2 Eşitsizliği çöz: .
Eşitsizlikleri grafik bir yöntemle çözerken, fonksiyonların grafiklerini olabildiğince doğru bir şekilde oluşturmak gerekir. Eşitsizliği forma dönüştürelim:
Bir koordinat sisteminde fonksiyonların grafiklerini oluşturalım. 
Ve 
(İncir. 2).
İncir. 2
Fonksiyon grafikleri bir noktada kesişirA
koordinatlı 
; 
. Arasında 
grafik noktaları 
grafik noktalarının altında 
. Ve ne zaman fonksiyon değerleri aynıdır. Bu yüzden de 
.
Cevap: 
.
1.3. cebirsel yöntem
Çoğu zaman, orijinal trigonometrik eşitsizlik, iyi seçilmiş bir ikame ile cebirsel (rasyonel veya irrasyonel) bir eşitsizliğe indirgenebilir. Bu yöntem, eşitsizliğin dönüştürülmesini, bir ikamenin getirilmesini veya bir değişkenin değiştirilmesini içerir.
Bu yöntemin uygulamasını somut örnekler üzerinde ele alalım.
Örnek 3
En basit forma indirgeme 
.
(Şek. 3)
Şek. 3
, 
.
Cevap: 
,
Örnek 4 Eşitsizliği çözün:
ODZ: 
, 
.
Formülleri kullanma: 
, 
eşitsizliği şu şekilde yazarız: 
.
Veya varsayarak 
basit dönüşümlerden sonra elde ederiz
,
,
.
Son eşitsizliği aralık yöntemiyle çözerek şunu elde ederiz:
Şekil 4
, sırasıyla 
. Daha sonra Şekil. 4 takip 
, Nerede 
.
Şekil 5
Cevap: 
, 
.
1.4. Aralık yöntemi
Aralık yöntemiyle trigonometrik eşitsizlikleri çözmek için genel şema:
Trigonometrik formülleri kullanarak çarpanlara ayırın.
Fonksiyonun kesme noktalarını ve sıfırlarını bulun, dairenin üzerine koyun.
Herhangi bir noktayı alİLE (ancak daha önce bulunamadı) ve ürünün işaretini öğrenin. Çarpım pozitif ise, açıya karşılık gelen ışın üzerinde birim çemberin dışında bir nokta koyun. Aksi takdirde, noktayı dairenin içine koyun.
Eğer bir nokta çift sayıda oluyorsa, buna çift çokluk noktası, tek sayıda ise, tek çokluk noktası diyoruz. Yayları şu şekilde çizin: bir noktadan başlayınİLE , bir sonraki nokta tek çokluksa, yay bu noktada daireyi keser, ancak nokta çift çokluksa, o zaman kesişmez.
Bir dairenin arkasındaki yaylar pozitif boşluklardır; dairenin içinde negatif aralıklar var.
Örnek 5 eşitsizliği çöz
, 
.
İlk serinin puanları: 
.
İkinci serinin puanları: 
.
Her nokta, tek sayıda, yani tek çokluğun tüm noktalarında meydana gelir.
Ürünün işaretini adresinde bulabilirsiniz. 
: . Birim çember üzerindeki tüm noktaları işaretliyoruz (Şek. 6):
Pirinç. 6
Cevap: 
, 
; 
, 
; 
, 
.
Örnek 6 . eşitsizliği çöz.
Çözüm:
ifadesinin sıfırlarını bulalım. .
Elde etmekaeM :
,
;
, 
;
, 
;
, 
;
Birim çember üzerinde seri değerlerX
1
noktalarla temsil edilir 
. SeriX
2
puan verir 
. Bir diziX
3
iki puan alırız 
. Sonunda bir diziX
4
noktaları temsil edecek 
. Tüm bu noktaları, çokluğunun yanında parantez içinde göstererek birim çemberin üzerine koyuyoruz.
Şimdi sayı olsun 
eşit olacaktır. İşarete göre bir tahmin yapıyoruz:
Yani noktaA
açı oluşturan kiriş üzerinde seçilmelidir 
kirişliAh,
birim çemberin dışında. (Yardımcı kirişinHAKKINDA
A
resimde gösterilmesi gerekmiyor. NoktaA
yaklaşık olarak seçilir.)
Şimdi noktadanA
işaretli tüm noktalara sırayla dalgalı sürekli bir çizgi çiziyoruz. Ve noktalarda çizgimiz bir bölgeden diğerine geçer: eğer birim çemberin dışındaysa, o zaman ona geçer. Noktaya yaklaşmak 
, bu noktanın çokluğu çift olduğu için çizgi iç bölgeye geri döner. Aynı şekilde noktada 
(çift çoklukta) çizginin dış bölgeye döndürülmesi gerekir. Böylece, Şekil l'de gösterilen belirli bir resim çizdik. 7. Birim çember üzerinde istenilen bölgelerin vurgulanmasına yardımcı olur. Bir "+" ile işaretlenirler.
Şekil 7
Son cevap:
Not. Dalgalı çizgi, birim çember üzerinde işaretlenmiş tüm noktaları geçtikten sonra noktaya geri döndürülemezseA , daireyi "geçersiz" bir yerde kesmeden, bu, çözümde bir hata yapıldığı, yani tek sayıda kökün atlandığı anlamına gelir.
Cevap: .
§2. Trigonometrik eşitsizlikleri çözmek için bir dizi görev
Okul çocuklarının trigonometrik eşitsizlikleri çözme becerilerini geliştirme sürecinde 3 aşama da ayırt edilebilir.
1. hazırlık,
2. en basit trigonometrik eşitsizlikleri çözmek için becerilerin oluşturulması;
3. Diğer türlerdeki trigonometrik eşitsizliklerin tanıtılması.
Hazırlık aşamasının amacı, okul çocuklarında eşitsizlikleri çözmek için trigonometrik bir daire veya grafik kullanma becerisinin oluşturulması gerektiğidir, yani:
Formun basit eşitsizliklerini çözebilme ,
, ,
,
sinüs ve kosinüs fonksiyonlarının özelliklerini kullanma;
Sayısal bir dairenin yayları veya fonksiyon grafiklerinin yayları için çifte eşitsizlik yapabilme;
Trigonometrik ifadelerin çeşitli dönüşümlerini gerçekleştirme becerisi.
Okul çocuklarının trigonometrik fonksiyonların özellikleri hakkındaki bilgilerini sistematik hale getirme sürecinde bu aşamanın uygulanması önerilir. Ana araçlar, öğrencilere sunulan ve bir öğretmenin rehberliğinde veya bağımsız olarak gerçekleştirilen görevler ve ayrıca trigonometrik denklemleri çözmede kazanılan beceriler olabilir.
İşte bu tür görevlere örnekler:
1
. Birim çember üzerinde bir nokta işaretleyin 
, Eğer
.
2.
noktası koordinat düzleminin hangi çeyreğindedir? , Eğer 
eşittir: 
3.
Trigonometrik daire üzerindeki noktaları işaretleyin , Eğer:
4. İfadeyi trigonometrik fonksiyonlara getirinBENçeyreklik.
A) 
,
B) 
,
v) 
5. MR arkı göz önüne alındığında.M - ortaBENçeyrek,R - ortaIIIçeyrek. Bir değişkenin değerini kısıtlamaT için: (bir çift eşitsizlik oluşturun) a) ark MP; b) RM yayları.
6. Grafiğin seçilen bölümleri için bir çift eşitsizlik yazın:
Pirinç. 1
7.
eşitsizlikleri çöz 
, 
, 
, 
.
8. İfadeyi dönüştür .
Trigonometrik eşitsizlikleri çözmeyi öğrenmenin ikinci aşamasında, öğrenci etkinliklerini düzenleme yöntemiyle ilgili olarak aşağıdaki önerileri sunabiliriz. Aynı zamanda, öğrencilerin en basit trigonometrik denklemlerin çözümü sırasında oluşan trigonometrik daire veya grafik ile çalışma becerilerine odaklanmak gerekir.
İlk olarak, en basit trigonometrik eşitsizlikleri çözmek için genel bir yöntem elde etmenin uygunluğunu, örneğin bir form eşitsizliğine atıfta bulunarak motive etmek mümkündür. 
.
Öğrenciler hazırlık aşamasında edindikleri bilgi ve becerileri kullanarak önerilen eşitsizliği forma getireceklerdir. 
, ancak ortaya çıkan eşitsizliğe bir dizi çözüm bulmak zor olabilir, çünkü sadece sinüs fonksiyonunun özelliklerini kullanarak çözmek imkansızdır. Bu zorluk, uygun resme başvurarak önlenebilir (denklemin grafiksel olarak çözümü veya birim çember kullanılarak).
İkinci olarak, öğretmen öğrencilerin dikkatini görevi tamamlamanın farklı yollarına çekmeli, hem grafiksel olarak hem de trigonometrik daireyi kullanarak eşitsizliği çözmek için uygun bir örnek vermelidir.
Eşitsizliği çözmek için bu tür seçenekleri göz önünde bulundurun .
1. Eşitsizliği birim çemberi kullanarak çözme.
Trigonometrik eşitsizlikleri çözme konusundaki ilk derste, öğrencilere eşitsizliği çözmek için gerekli tüm temel becerileri adım adım yansıtan ayrıntılı bir çözüm algoritması sunacağız.
Aşama 1.Bir birim daire çizin, y ekseninde bir nokta işaretleyin 
ve içinden x eksenine paralel düz bir çizgi çizin. Bu doğru birim çemberi iki noktada keser. Bu noktaların her biri, sinüsü şuna eşit olan sayıları gösterir: .
Adım 2Bu düz çizgi daireyi iki yaya böldü. Sinüsü şundan büyük olan sayıların gösterildiğini seçelim: . Doğal olarak, bu yay çizilen düz çizginin üzerinde bulunur.
Pirinç. 2
Aşama 3İşaretli yayın uçlarından birini seçelim. Birim çemberin bu noktasının temsil ettiği sayılardan birini yazalım. 
.
Adım 4Seçilen yayın ikinci ucuna karşılık gelen bir sayı seçmek için, bu yay boyunca belirtilen uçtan diğerine "geçeriz". Aynı zamanda saat yönünün tersine hareket ettiğimizde geçeceğimiz sayıların arttığını (ters yönde hareket ettiğimizde sayıların azaldığını) hatırlıyoruz. İşaretli yayın ikinci ucunun birim çember üzerinde gösterdiği sayıyı yazalım. 
.
Böylece, eşitsizliğin olduğunu görüyoruz. eşitsizliğin olduğu sayıları tatmin etmek 
. Sinüs fonksiyonunun aynı periyodunda bulunan sayılar için eşitsizliği çözdük. Bu nedenle, eşitsizliğin tüm çözümleri şu şekilde yazılabilir: 
Öğrencilerden şekli dikkatli bir şekilde düşünmeleri ve neden eşitsizliğin tüm çözümlerini bulmaları istenmelidir. şeklinde yazılabilir. 
, 
.
Pirinç. 3
Kosinüs fonksiyonu için eşitsizlikleri çözerken y eksenine paralel düz bir çizgi çizdiğimize öğrencilerin dikkatini çekmek gerekir.
Eşitsizliği çözmenin grafik yolu.
Bina çizelgeleri 
Ve 
, verilen 
.
Pirinç. 4
sonra denklemi yazarız 
ve onun çözümü 
, 
, 
, formüller kullanılarak bulundu 
, 
, 
.
(VermekN
0, 1, 2 değerleri, oluşan denklemin üç kökünü buluruz). Değerler 
grafiklerin kesişme noktalarının ardışık üç apsisidir Ve . Açıkçası, her zaman aralıkta 
eşitsizlik 
, ve aralıkta 
- eşitsizlik 
. İlk durumla ilgileniyoruz ve sonra bu aralığın uçlarına sinüs periyodunun katı olan bir sayı ekleyerek eşitsizliğin bir çözümünü elde ediyoruz. gibi: 
, .
Pirinç. 5
Özetle. eşitsizliği çözmek için , karşılık gelen denklemi yazmanız ve çözmeniz gerekir. Ortaya çıkan formülden kökleri bulun 
Ve 
ve eşitsizliğin cevabını şu şekilde yazın: , .
Üçüncüsü, karşılık gelen trigonometrik eşitsizliğin kök kümesi hakkındaki gerçek, onu grafiksel olarak çözerken çok açık bir şekilde doğrulanır.
Pirinç. 6
Eşitsizliğin çözümü olan bobinin trigonometrik fonksiyonun periyodu kadar aynı aralıkta tekrar ettiğini öğrencilere göstermek gerekir. Sinüs fonksiyonunun grafiği için de benzer bir çizim düşünebilirsiniz.
Dördüncüsü, öğrencilerin trigonometrik fonksiyonların toplamını (farkını) bir ürüne dönüştürme yöntemlerini güncellemek, okul çocuklarının dikkatini bu tekniklerin trigonometrik eşitsizlikleri çözmedeki rolüne çekmek için çalışmalar yapılması tavsiye edilir.
Bu tür çalışmalar, öğrencilerin öğretmen tarafından önerilen görevleri bağımsız olarak yerine getirmeleri yoluyla organize edilebilir ve aralarında aşağıdakileri vurgularız:
Beşincisi, öğrencilerden her basit trigonometrik eşitsizliğin çözümünü bir grafik veya trigonometrik daire kullanarak göstermeleri istenmelidir. Uygunluğuna, özellikle daire kullanımına dikkat ettiğinizden emin olun, çünkü trigonometrik eşitsizlikleri çözerken ilgili çizim, belirli bir eşitsizliğe çözüm kümesini sabitlemek için çok uygun bir araç görevi görür.
Öğrencilerin en basit olmayan trigonometrik eşitsizlikleri çözme yöntemleriyle tanışması, aşağıdaki şemaya göre yapılması tavsiye edilir: belirli bir trigonometrik eşitsizliğe atıfta bulunarak karşılık gelen trigonometrik denkleme atıfta bulunarak bağımsız bir çözüm için ortak arama (öğretmen - öğrenciler) bulunan tekniğin aynı türdeki diğer eşitsizliklere aktarımı.
Öğrencilerin trigonometri bilgilerini sistematik hale getirmek için, çözümü sürecinde uygulanabilecek çeşitli dönüşümler gerektiren bu tür eşitsizlikleri özellikle seçmenizi ve öğrencilerin dikkatini özelliklerine odaklamanızı öneririz.
Bu tür üretken eşitsizlikler olarak, örneğin aşağıdakileri önerebiliriz:
Sonuç olarak, trigonometrik eşitsizlikleri çözmek için bir dizi problem örneği veriyoruz.
1. Eşitsizlikleri çözün:
2. Eşitsizlikleri çözün: 3. Eşitsizliklerin tüm çözümlerini bulun: 4. Eşitsizliklerin tüm çözümlerini bulun:A) 
, koşulu sağlayan 
;
B) 
, koşulu sağlayan 
.
5. Eşitsizliklerin tüm çözümlerini bulun:
A) ;
B) ;
v) 
;
G) 
;
e) 
.
6. Eşitsizlikleri çözün:
A) ;
B) ;
v) ;
G) 
;
e) ;
e) ;
Ve) 
.
7. Eşitsizlikleri çözün:
A) 
;
B) ;
v) ;
G) .
8. Eşitsizlikleri çözün:
A) ;
B) ;
v) ;
G) 
;
e) 
;
e) ;
Ve) 
;
H) .
İleri düzeyde matematik okuyan öğrencilere 6. ve 7. görevlerin, derinlemesine matematik çalışması olan sınıflardaki öğrencilere 8. görevin verilmesi önerilir.
§3. Trigonometrik eşitsizlikleri çözmek için özel yöntemler
Trigonometrik denklemleri çözmek için özel yöntemler - yani, yalnızca trigonometrik denklemleri çözmek için kullanılabilecek yöntemler. Bu yöntemler, trigonometrik fonksiyonların özelliklerinin kullanımına ve ayrıca çeşitli trigonometrik formüllerin ve özdeşliklerin kullanımına dayanmaktadır.
3.1. Sektör Yöntemi
Trigonometrik eşitsizlikleri çözmek için sektör yöntemini düşünün. Formun eşitsizliklerinin çözümü 
, NeredeP
(
X
)
VeQ
(
X
)
– rasyonel trigonometrik fonksiyonlar(sinüsler, kosinüsler, teğetler ve kotanjantlar bunlara rasyonel olarak girer), rasyonel eşitsizliklerin çözümüne benzer şekilde. Rasyonel eşitsizlikleri gerçek eksende aralıklar yöntemiyle çözmek uygundur. Rasyonel trigonometrik eşitsizlikleri çözmedeki analogu, trigonometrik bir dairedeki sektörler yöntemidir, çünküsinx
Vecosx
(
) veya trigonometrik yarım daire içintgx
Vectgx
(
).
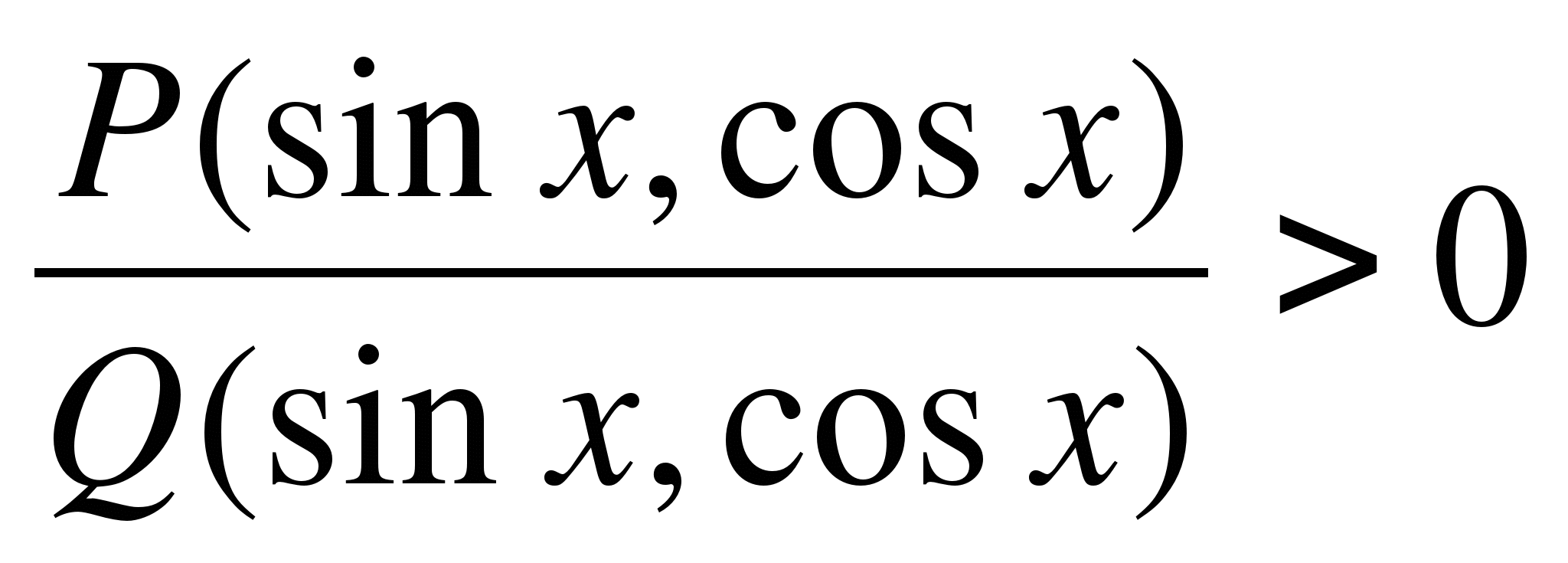
Aralık yönteminde, formun pay ve paydasının her bir doğrusal faktörü 
sayı ekseni üzerinde nokta 
ve bu noktadan geçerken işareti değiştirir. Sektör yönteminde, formun her çarpanı 
, Nerede 
- işlevlerden birisinx
veyacosx
Ve 
, trigonometrik bir çemberde iki açıya karşılık gelir 
Ve 
, daireyi iki sektöre böler. geçerken Ve işlev işareti değiştirir.
Aşağıdakiler hatırlanmalıdır:
a) Formun çarpanları 
Ve 
, Nerede 
, tüm değerler için işareti koru 
. Pay ve paydanın bu tür çarpanları atılır, değiştirilir (eğer 
) bu tür her reddetmede, eşitsizlik işareti tersine çevrilir.
b) Formun çarpanları 
Ve 
da atılır. Dahası, eğer bunlar paydanın faktörleri ise, o zaman formdaki eşitsizlikler eşdeğer eşitsizlik sistemine eklenir. 
Ve 
. Bunlar payın faktörleriyse, eşdeğer kısıtlama sisteminde eşitsizliklere karşılık gelirler. Ve kesin ilk eşitsizlik ve eşitlik durumunda 
Ve 
kesin olmayan bir ilk eşitsizlik durumunda. Çarpanı düşürürken 
veya 
eşitsizlik işareti tersine çevrilir.
örnek 1
Eşitsizlikleri çözün: a) 
, B) 
.
bir fonksiyonumuz var, b). Elimizdeki eşitsizliği çöz
3.2. Eşmerkezli daire yöntemi
Bu yöntem, rasyonel eşitsizlik sistemlerinin çözümünde paralel sayısal eksenler yöntemine benzer.
Bir eşitsizlik sistemi örneğini ele alalım.
Örnek 5
Basit bir trigonometrik eşitsizlik sistemini çözün 
Öncelikle her bir eşitsizliği ayrı ayrı çözüyoruz (Şekil 5). Şeklin sağ üst köşesinde, trigonometrik dairenin hangi argüman için dikkate alındığını belirteceğiz.
Şekil 5
Ardından, argüman için eşmerkezli çemberlerden oluşan bir sistem oluşturuyoruz.X . Birinci eşitsizliğin çözümüne göre bir çember çizip gölgelendiriyoruz, sonra yarıçapı büyük bir çember çizip ikincinin çözümüne göre gölgelendiriyoruz, ardından üçüncü eşitsizlik için bir çember ve bir taban çemberi oluşturuyoruz. . Sistemin merkezinden yayların uçlarından geçerek tüm çemberleri kesecek şekilde ışınlar çiziyoruz. Taban çemberi üzerinde bir çözüm oluşturuyoruz (Şekil 6).
Şekil 6
Cevap:
, 
.
Çözüm
Kursun tüm hedefleri tamamlandı. Teorik materyal sistematikleştirilmiştir: ana trigonometrik eşitsizlik türleri ve bunların çözümü için ana yöntemler (grafik, cebirsel, aralıklar yöntemi, sektörler ve eşmerkezli daireler yöntemi) verilmektedir. Her yöntem için bir eşitsizliğin çözümüne ilişkin bir örnek verilmiştir. Teorik kısmı pratik kısım takip etti. Trigonometrik eşitsizlikleri çözmek için bir dizi görev içerir.
Bu kurs, öğrenciler tarafından şu amaçlarla kullanılabilir: bağımsız iş. Öğrenciler, bu konunun özümseme düzeyini kontrol edebilir, değişen karmaşıklıktaki görevleri yerine getirme alıştırması yapabilir.
Bu konuda ilgili literatürü inceledikten sonra, okul cebir dersinde ve analizin başlangıcında trigonometrik eşitsizlikleri çözme beceri ve becerilerinin çok önemli olduğu sonucuna varabiliriz ve geliştirilmesi büyük çaba gerektirir. matematik öğretmeni.
Bu nedenle, bu çalışma öğrencilerin "Trigonometrik eşitsizlikler" konusundaki eğitimini etkin bir şekilde organize etmeyi mümkün kıldığından matematik öğretmenleri için faydalı olacaktır.
Çalışma, nihai eleme çalışmasına kadar genişletilerek devam ettirilebilir..
Kullanılan literatür listesi
Bogomolov, N.V. Matematik problemlerinin toplanması [Metin] / N.V. Bogomolov. – M.: Bustard, 2009. – 206 s.
Vygodsky, M.Ya. Temel matematik el kitabı [Metin] / M.Ya. Vygodsky. – M.: Bustard, 2006. – 509 s.
Zhurbenko, L.N. Örneklerde ve görevlerde matematik [Metin] / L.N. Zhurbenko. – M.: Infra-M, 2009. – 373 s.
Ivanov, O.A. Okul çocukları, öğrenciler ve öğretmenler için temel matematik [Metin] / O.A. İvanov. – M.: MTsNMO, 2009. – 384 s.
Karp, AP Cebirdeki görevler ve 11. sınıfta son tekrar ve sertifikasyonun organizasyonu için analizin başlangıcı [Metin] / A.P. Sazan. – M.: Aydınlanma, 2005. – 79 s.
Kulanin, E.D. Matematikte 3000 rekabet problemi [Metin] / E.D. Kulanin. – M.: Iris-press, 2007. – 624 s.
Leibson, KL Toplamak pratik görevler matematikte [Metin] / K.L. Leibson. – M.: Bustard, 2010. – 182 s.
Dirsek, V.V. Parametrelerle ilgili problemler ve çözümleri. Trigonometri: denklemler, eşitsizlikler, sistemler. 10. Sınıf [Metin] / V.V. Dirsek. – M.: ARKTI, 2008. – 64 s.
Manova, A.N. Matematik. Sınava hazırlanmak için ekspres öğretmen: hesap. ödenek [Metin] / A.N. Manova. - Rostov-on-Don: Phoenix, 2012. - 541 s.
Mordkoviç, A.G. Cebir ve matematiksel analizin başlangıcı. 10-11 sınıflar. Eğitim kurumlarının öğrencileri için ders kitabı [Metin] / A.G. Mordkoviç. – M.: Iris-press, 2009. – 201 s.
Novikov, A.I. Trigonometrik fonksiyonlar, denklemler ve eşitsizlikler [Metin] / A.I. Novikov. - M.: FİZMATLİT, 2010. - 260 s.
Oganesyan, V.A. Ortaokulda matematik öğretme yöntemleri: Genel metodoloji. Proc. fizik öğrencileri için ödenek. - mat. fak. ped. yoldaş [Metin] / V.A. Oganesyan. – M.: Aydınlanma, 2006. – 368 s.
Olechnik, S.N. Denklemler ve eşitsizlikler. Standart olmayan çözüm yöntemleri [Metin] / S.N. Olekhnik. - M .: Yayınevi Factorial, 1997. - 219 s.
Sevryukov, P.F. Trigonometrik, üstel ve logaritmik denklemler ve eşitsizlikler [Metin] / P.F. Sevryukov. – M.: Milli Eğitim, 2008. – 352 s.
Sergeev, I.N. KULLANIM: Matematikte cevapları ve çözümleri olan 1000 görev. C grubunun tüm görevleri [Metin] / I.N. Sergeev. – M.: Sınav, 2012. – 301 s.
Sobolev, A.B. Temel matematik [Metin] / A.B. Sobolev. - Yekaterinburg: GOU VPO USTU-UPI, 2005. - 81 s.
Fenko, L.M. Eşitsizlikleri çözmede ve fonksiyonları incelemede aralık yöntemi [Metin] / L.M. Fenko. – M.: Bustard, 2005. – 124 s.
Friedman, L.M. teorik temel matematik öğretme yöntemleri [Metin] / L.M. Friedman. - M .: Kitap evi "LIBROKOM", 2009. - 248 s.
Ek 1
En basit eşitsizliklerin çözümlerinin grafiksel yorumu
Pirinç. 1
Pirinç. 2
Şek. 3
Şekil 4
Şekil 5
Şekil 6
Şekil 7
Şekil 8
Ek 2
En basit eşitsizliklerin çözümleri
Belarus Cumhuriyeti Eğitim Bakanlığı
Eğitim kurumu
"Gomel Devlet Üniversitesi
adını Francysk Skaryna'dan almıştır"
Matematik Fakültesi
Cebir ve Geometri Bölümü
Savunma için uygun
KAFA Departman Shemetkov L.A.
Trigonometrik denklemler ve eşitsizlikler
Ders çalışması
yürütücü:
öğrenci grubu M-51
SANTİMETRE. Gorski
Bilim danışmanı
Kıdemli okutman
VG Safonov
Gomel 2008
GİRİİŞ
TRİGONOMETRİK DENKLEMLERİ ÇÖZMEK İÇİN TEMEL YÖNTEMLER
çarpanlara ayırma
Trigonometrik fonksiyonların çarpımını bir toplama çevirerek denklemleri çözme
Üçlü Argüman Formüllerini Kullanarak Denklemleri Çözme
Bazı trigonometrik fonksiyonlarla çarpma
STANDART OLMAYAN TRİGONOMETRİK DENKLEMLER
TRİGONOMETRİK EŞİTSİZLİKLER
KÖK SEÇİMİ
BAĞIMSIZ ÇÖZÜM İÇİN GÖREVLER
ÇÖZÜM
KULLANILAN KAYNAKLAR LİSTESİ
Eski zamanlarda, trigonometri astronomi, ölçme ve inşaat ihtiyaçları ile bağlantılı olarak ortaya çıktı, yani doğası gereği tamamen geometrikti ve esas olarak temsil edildi.<<исчисление хорд>>. Zamanla, bazı analitik noktalar onun içine serpiştirmeye başladı. 18. yüzyılın ilk yarısında keskin bir dönüş oldu, ardından trigonometri yeni bir yön aldı ve matematiksel analize doğru kaydı. Bu sırada trigonometrik bağımlılıklar fonksiyon olarak kabul edilmeye başlandı.
Trigonometrik denklemler, okul matematik dersindeki en zor konulardan biridir. Planimetri, katı geometri, astronomi, fizik ve diğer alanlardaki problemleri çözerken trigonometrik denklemler ortaya çıkar. Trigonometrik denklemler ve yıldan yıla eşitsizlikler, merkezi testin görevleri arasında bulunur.
Trigonometrik ve cebirsel denklemler arasındaki en önemli fark, cebirsel denklemlerin sınırlı sayıda köke sahip olması, trigonometrik denklemlerin ise sonsuz sayıda kök seçimini büyük ölçüde zorlaştırmasıdır. Trigonometrik denklemlerin bir diğer özelliği, cevabı yazmanın benzersiz olmayan şeklidir.
Bu tez, trigonometrik denklemleri ve eşitsizlikleri çözme yöntemlerine ayrılmıştır.
Diploma çalışması 6 bölümden oluşmaktadır.
İlk bölüm temel teorik bilgileri içerir: trigonometrik ve ters trigonometrik fonksiyonların tanımı ve özellikleri; bazı argümanlar için trigonometrik fonksiyonların değer tablosu; trigonometrik ifadelerin dönüştürülmesi için çok önemli olan trigonometrik fonksiyonların diğer trigonometrik fonksiyonlar cinsinden ifadesi, özellikle ters trigonometrik fonksiyonları içerenler; okul dersinden iyi bilinen temel trigonometrik formüllere ek olarak, ters trigonometrik fonksiyonları içeren ifadeleri basitleştiren formüller verilir.
İkinci bölüm, trigonometrik denklemleri çözmek için ana yöntemleri özetlemektedir. Temel trigonometrik denklemlerin çözümü, faktoring yöntemi, trigonometrik denklemleri cebirsel denklemlere indirgeme yöntemleri ele alınır. Trigonometrik denklemlerin çözümlerinin birkaç şekilde yazılabileceği ve bu çözümlerin şeklinin, bu çözümlerin aynı mı yoksa farklı mı olduğunu hemen belirlemeye izin vermediği göz önüne alındığında,<<сбить с толку>> testleri çözerken, trigonometrik denklemleri çözmek için genel bir şema dikkate alınır ve trigonometrik denklemlerin genel çözüm gruplarının dönüşümü ayrıntılı olarak ele alınır.
Üçüncü bölüm, çözümleri fonksiyonel yaklaşıma dayanan standart olmayan trigonometrik denklemlerle ilgilidir.
Dördüncü bölüm trigonometrik eşitsizliklerle ilgilidir. Temel trigonometrik eşitsizlikleri hem birim çember üzerinde hem de grafik yöntemle çözme yöntemleri ayrıntılı olarak ele alınmıştır. Temel olmayan trigonometrik eşitsizlikleri temel eşitsizlikler yoluyla çözme süreci ve okul çocukları tarafından zaten iyi bilinen aralıklar yöntemi açıklanmaktadır.
Beşinci bölüm en zor görevleri sunar: sadece bir trigonometrik denklemi çözmek değil, aynı zamanda bulunan köklerden bazı koşulları sağlayan kökleri seçmek gerektiğinde. Bu bölüm, köklerin seçimine yönelik tipik görevlere yönelik çözümler sağlar. Köklerin seçimi için gerekli teorik bilgiler verilir: tamsayılar kümesinin kesişmeyen alt kümelere bölünmesi, tamsayılarda denklemlerin çözümü (diophantine).
Altıncı bölüm, test şeklinde tasarlanmış bağımsız çözüm için görevler sunmaktadır. 20 test görevi, merkezi testte karşılaşılabilecek en zor görevleri listeler.
Temel trigonometrik denklemler
Temel trigonometrik denklemler, trigonometrik fonksiyonlardan birinin olduğu formdaki denklemlerdir: , , , .
Temel trigonometrik denklemlerin sonsuz sayıda kökü vardır. Örneğin, aşağıdaki değerler denklemi karşılar: , , , vb. Denklemin tüm köklerinin bulunduğu genel formül, burada , şöyledir:
Burada herhangi bir tamsayı değeri alabilir, bunların her biri denklemin belirli bir köküne karşılık gelir; bu formülde (temel trigonometrik denklemlerin çözüldüğü diğer formüllerde olduğu gibi) denir parametre. Genellikle, parametrenin herhangi bir tamsayı değeri alabileceğini vurgulayarak bir yere yazarlar.
Denklemin çözümleri , nerede , formül tarafından bulunur
Denklem, formül uygulanarak çözülür
ve denklem --- formüle göre
Çözümün genel formüller kullanılmadan yazılabileceği temel trigonometrik denklemlerin bazı özel durumlarına özellikle dikkat edelim:
Trigonometrik denklemleri çözerken, trigonometrik fonksiyonların periyodu önemli bir rol oynar. Bu nedenle, iki yararlı teorem sunuyoruz:
teorem Eğer --- temel fonksiyonun periyodu, ardından sayı fonksiyonun ana periyodudur.
ve fonksiyonlarının periyotları orantılı olarak adlandırılır, eğer doğal sayılar varsa ve , that .
teorem Periyodik fonksiyonlar ve , orantılıysa ve , o zaman ortak bir periyoda sahiptirler , bu da fonksiyonların periyodudur , , .
Teorem, , , fonksiyonunun periyodunun ne olduğunu söyler ve mutlaka ana periyot değildir. Örneğin, ve işlevlerinin ana periyodu --- ve çarpımlarının ana periyodu --- şeklindedir.
Yardımcı bağımsız değişkenin tanıtılması
Formun ifadelerini dönüştürmenin standart yolu 
şu numara: izin ver --- köşe, eşitlikler tarafından verilir 
, 
. Herhangi biri için böyle bir açı vardır. Böylece . Aksi takdirde , veya , , , ise .
Trigonometrik denklemleri çözme şeması
Trigonometrik denklemleri çözerken rehberlik edeceğimiz ana şema aşağıdaki gibidir:
verilen denklemin çözümü temel denklemlerin çözümüne indirgenir. Çözümler --- dönüşümler, çarpanlara ayırma, bilinmeyenlerin yer değiştirmesi. Yol gösterici ilke kökleri kaybetmemektir. Bu, bir sonraki denkleme (denklemlere) geçerken, fazladan (dış) köklerin ortaya çıkmasından korkmadığımız, yalnızca her birinin sonraki denklem"zincirimiz" (veya dallanma durumunda denklemler dizimiz) bir öncekinin sonucuydu. Kökleri seçmek için olası bir yöntem kontrol etmektir. Trigonometrik denklemler söz konusu olduğunda, köklerin seçimi ile ilgili zorlukların, kural olarak doğrulama ile cebirsel denklemlere kıyasla keskin bir şekilde arttığını hemen not ediyoruz. Sonuçta sonsuz sayıda üyeden oluşan seriyi kontrol etmeniz gerekiyor.
Trigonometrik denklemlerin çözümünde bilinmeyenlerin değişimine özel olarak değinilmelidir. Çoğu durumda, gerekli değiştirmeden sonra cebirsel bir denklem elde edilir. Ayrıca, görünüşte trigonometrik olmalarına rağmen aslında öyle olmayan denklemler için nadir değildir, çünkü ilk adımdan sonra --- değiştirmeler değişkenler --- cebirsel olanlara dönüşür ve trigonometriye dönüş yalnızca temel trigonometrik denklemleri çözme aşamasında gerçekleşir.
Bir kez daha hatırlatalım: bilinmeyenin yer değiştirmesi bir an önce yapılmalı, yer değiştirmeden sonra elde edilen denklem köklerin seçilmesi aşaması da dahil olmak üzere sonuna kadar çözülmeli ve ancak o zaman aslına dönecektir. Bilinmeyen.
Trigonometrik denklemlerin özelliklerinden biri, birçok durumda cevabın çeşitli şekillerde yazılabilmesidir. Denklemi çözmek için bile 
yanıt şu şekilde yazılabilir:
1) iki seri halinde: 
, , ;
2) yukarıdaki serilerin birleşimi olan standart formda: , ;
3) beri 
, o zaman cevap olarak yazılabilir 
, . (Ayrıca, yanıt kaydında , veya parametresinin varlığı otomatik olarak bu parametrenin tüm olası tamsayı değerleri aldığı anlamına gelir. İstisnalar şart koşulacaktır.)
Açıkçası, listelenen üç durum, dikkate alınan denklemin cevabını yazmak için tüm olasılıkları tüketmez (sonsuz sayıda vardır).
Örneğin, için 
. Bu nedenle, ilk iki durumda, if yerine şunu koyabiliriz: .
Genellikle cevap 2. paragrafa göre yazılır. Aşağıdaki tavsiyeyi hatırlamakta fayda var: eğer iş denklemin çözümü ile bitmiyorsa, yine de bir çalışma yapmak, kökleri seçmek, sonra en uygun kayıt şekli 1. paragrafta belirtilmiştir. (Benzer bir öneri denklem için verilmelidir.)
Söylenenleri açıklayan bir örnek ele alalım.
Örnek Denklemi çözün.
Çözüm. En bariz olanı aşağıdaki yoldur. Bu denklem ikiye ayrılır: ve . Her birini çözerek ve elde edilen cevapları birleştirerek buluyoruz.
Diğer yol. O zamandan beri, ve değiştirme formülleri ile. Küçük dönüşümlerden sonra, nereden 
.
İlk bakışta, ikinci formülün birinciye göre belirli bir avantajı yoktur. Bununla birlikte, örneğin, alırsak, o zaman ortaya çıkar ki, yani. denklemin bir çözümü vardır, birinci yol ise bizi cevaba götürür 
. "Gör" ve eşitliği kanıtla 
çok kolay değil.
Cevap. .
Trigonometrik denklemlerin genel çözüm gruplarının dönüşümü ve birleşimi
Düşüneceğiz aritmetik ilerleme her iki yönde de sonsuza kadar uzanır. Bu ilerlemenin terimleri, ilerlemenin merkezi veya sıfır terimi olarak adlandırılan belirli bir terimin sağında ve solunda bulunan iki terim grubuna ayrılabilir.
Sonsuz ilerlemenin terimlerinden birini sıfırla sabitleyerek, kalan tüm terimler için çift numaralandırma yapmamız gerekecek: sağda bulunan terimler için pozitif ve sıfırın solunda bulunan terimler için negatif.
Genel durumda, ilerleme farkı sıfır terim ise, sonsuz aritmetik ilerlemenin herhangi bir (th) terimi için formül şöyledir:
Sonsuz bir aritmetik ilerlemenin herhangi bir üyesi için formül dönüşümleri
1. İlerleme farkını sıfır terime ekler veya çıkarırsak, ilerleme bundan değişmez, sadece sıfır terim hareket eder, yani. üye sayısı değişecektir.
2. Eğer katsayı değişken ile çarparsanız, bundan yalnızca sağ ve sol terim gruplarının bir permütasyonu meydana gelir.
3. Sonsuz bir ilerlemenin ardışık üyeleri ise
örneğin , , , ..., , aynı farkla ilerlemelerin merkezi terimlerini şuna eşitlemek için:
o zaman ilerleme ve ilerleme dizisi aynı sayıları ifade eder.
Örnek Satır aşağıdaki üç satırla değiştirilebilir: , , .
4. Aynı farka sahip sonsuz ilerlemelerin, farkla aritmetik bir dizi oluşturan merkezi üyeler olarak sayıları varsa, bu seriler, farkla tek bir dizi ile ve bunların merkezi üyelerinden herhangi birine eşit bir merkezi üye ile değiştirilebilir. ilerlemeler, yani Eğer
daha sonra bu ilerlemeler tek bir ilerlemede birleştirilir:
Örnek
, , , her ikisi de tek bir grupta birleştirilir, çünkü 
.
Çözümleri ortak olan grupları, ortak çözümleri olmayan gruplara dönüştürmek için, bu gruplar ortak periyoda sahip gruplara ayrıştırılır ve daha sonra ortaya çıkan grupları, tekrar edenleri hariç tutarak birleştirmeye çalışırız.
çarpanlara ayırma
Çarpanlara ayırma yöntemi şu şekildedir: eğer
o zaman denklemin herhangi bir çözümü
denklem setinin çözümü
Ters ifade genel olarak yanlıştır: kümenin her çözümü denklemin çözümü değildir. Bunun nedeni, bireysel denklemlerin çözümlerinin fonksiyonun tanım alanına dahil edilememesidir.
Örnek Denklemi çözün.
Çözüm. Temel trigonometrik özdeşliği kullanarak, denklemi şu şekilde temsil ederiz:
Cevap.
; 
.
Trigonometrik fonksiyonların toplamını bir ürüne dönüştürme
Örnek
denklemi çözün 
.
Çözüm. Formülü uyguluyoruz, eşdeğer bir denklem elde ediyoruz
Cevap. .
Örnek Denklemi çözün.
Çözüm. Bu durumda, trigonometrik fonksiyonların toplamı için formülleri uygulamadan önce, indirgeme formülünü kullanmalısınız. 
. Sonuç olarak, eşdeğer bir denklem elde ederiz
Cevap.
, 
.
Trigonometrik fonksiyonların çarpımını bir toplama çevirerek denklemleri çözme
Bir dizi denklemi çözerken, formüller kullanılır.
Örnek denklemi çözün
Çözüm.
Cevap. , .
Örnek Denklemi çözün.
Çözüm. Formülü uygulayarak eşdeğer bir denklem elde ederiz:
Cevap. .
İndirgeme Formüllerini Kullanarak Denklemleri Çözme
Çok çeşitli trigonometrik denklemleri çözerken, formüller önemli bir rol oynar.
Örnek Denklemi çözün.
Çözüm. Formülü uygulayarak eşdeğer bir denklem elde ederiz.
Cevap. ; .
Üçlü Argüman Formüllerini Kullanarak Denklemleri Çözme
Örnek Denklemi çözün.
Çözüm. Formülü uyguluyoruz, denklemi elde ediyoruz
Cevap. ; .
Örnek
denklemi çözün 
.
Çözüm. Dereceyi düşürmek için formülleri uygulayarak şunu elde ederiz: 
. Başvururken şunları elde ederiz:
Cevap. ; .
Aynı isimli trigonometrik fonksiyonların eşitliği
Örnek Denklemi çözün.
Çözüm.
Cevap. , .
Örnek
denklemi çözün 
.
Çözüm. Denklemi dönüştürelim.
Cevap. .
Örnek Denklemi sağladığı biliniyor ve
Toplamı bulun.
Çözüm. Denklemden şu çıkar:
Cevap. .
Formun toplamlarını düşünün
Bu toplamlar, çarpılıp bölünerek bir ürüne dönüştürülebilir, sonra şunu elde ederiz:
Bu teknik, bazı trigonometrik denklemleri çözmek için kullanılabilir, ancak sonuç olarak yabancı köklerin ortaya çıkabileceği akılda tutulmalıdır. İşte bu formüllerin bir genellemesi:
Örnek Denklemi çözün.
Çözüm. Kümenin orijinal denklemin bir çözümü olduğu görülebilir. Bu nedenle, denklemin sol ve sağ taraflarını ile çarpmak fazladan kök görünümüne yol açmaz.
Sahibiz 
.
Cevap. ; .
Örnek Denklemi çözün.
Çözüm. Denklemin sol ve sağ taraflarını ile çarparız ve trigonometrik fonksiyonların çarpımını bir toplama dönüştürmek için formülleri uygularız, elde ederiz
Bu denklem, iki denklem kümesine eşdeğerdir ve , buradan ve .
Denklemin kökleri, denklemin kökleri olmadığından, sonuçta ortaya çıkan çözüm kümelerinden çıkarılmalıdır. Yani sette dışlamanız gerekir .
Cevap. Ve , .
Örnek
denklemi çözün 
.
Çözüm. ifadeyi dönüştürelim:
Denklem şu şekilde yazılacaktır:
Cevap. .
Trigonometrik denklemlerin cebirsel denklemlere indirgenmesi
kareye indirgemek
Denklem gibi görünüyorsa
sonra değiştirme onu bir kareye getirir, çünkü 
() Ve.
Terim yerine varsa, o zaman gerekli değiştirme olacaktır.
Denklem
indirgenir ikinci dereceden denklem
olarak sunum 
. Denklemin kökleri olmadığını kontrol etmek kolaydır ve değişikliği yaparak denklem ikinci dereceden bir denkleme indirgenir.
Örnek Denklemi çözün.
Çözüm. Sol tarafa taşıyalım, ile değiştirelim ve ile ifade edelim.
Sadeleştirmelerden sonra şunu elde ederiz: . Terimi terime bölün, ikameyi yapın:
dönersek, buluruz 
.
Denklemler,
Formun bir denklemini düşünün
burada , , , ..., , gerçek sayılardır. Denklemin sol tarafındaki her terimde, monomların dereceleri eşittir, yani sinüs ve kosinüs derecelerinin toplamı aynı ve eşittir. Böyle bir denklem denir homojen ve ile ilgili ve sayı çağrılır homojenlik göstergesi .
Açıktır ki, eğer , o zaman denklem şu şekli alacaktır:
kimin çözümleri hangi değerlerdir, yani sayılar , . Parantez içinde yazılan ikinci denklem de homojendir ancak dereceleri 1 daha düşüktür.
Eğer , o zaman bu sayılar denklemin kökleri değildir.
Aldığımızda: , ve denklemin (1) sol tarafı değerini alır.
Yani, için ve bu nedenle, denklemin her iki tarafı da ile bölünebilir. Sonuç olarak, denklemi elde ederiz:
ikame yoluyla kolayca cebirsel olana indirgenebilir:
Homojenlik indeksi 1 olan homojen denklemler. 'de, denklemimiz var.
Eğer , o zaman bu denklem , , denklemine eşdeğerdir, dolayısıyla , .
Örnek Denklemi çözün.
Çözüm. Bu denklem birinci dereceden homojendir. Her iki parçasını da bölerek şunu elde ederiz: , , , .
Cevap. .
Örnek noktasında, formun homojen bir denklemini elde ederiz.
Çözüm.
Denklemin her iki tarafını da bölersek, denklemi elde ederiz. 
, ikame ile kolayca bir kareye indirgenebilir: 
. Eğer 
, o zaman denklemin gerçel kökleri vardır , . Orijinal denklemin iki çözüm grubu olacaktır: , , .
Eğer 
, o zaman denklemin çözümü yoktur.
Örnek Denklemi çözün.
Çözüm. Bu denklem ikinci dereceden homojendir. Denklemin her iki tarafını da bölersek şunu elde ederiz: . Bırak o zaman , , . , , ; , , .
Cevap.
.
Denklem, formun bir denklemine indirgenir
Bunun için kimliği kullanmanız yeterlidir. 
Özellikle, denklem şu şekilde değiştirilirse homojen bir denkleme indirgenir: 
, o zaman eşdeğer denklemi elde ederiz:
Örnek Denklemi çözün.
Çözüm. Denklemi homojen hale getirelim:
Denklemin her iki tarafını da şuna bölün: 
, denklemi elde ederiz:
, o zaman ikinci dereceden denkleme gelelim: 
, , 
, 
, .
Cevap.
.
Örnek Denklemi çözün.
Çözüm. Pozitif değerlere sahip olduklarına göre, denklemin her iki tarafının da karesini alalım: , ,
izin ver, sonra alırız 
, , .
Cevap. .
Özdeşlikler Kullanılarak Çözülen Denklemler 
Aşağıdaki formülleri bilmek faydalıdır:
Örnek Denklemi çözün.
Çözüm. kullanarak, elde ederiz
Cevap.
Formüllerin kendilerini değil, onları türetmenin yolunu sunuyoruz:
buradan,
Aynı şekilde, .
Örnek
denklemi çözün 
.
Çözüm. ifadeyi dönüştürelim:
Denklem şu şekilde yazılacaktır:
alıyor, alıyoruz. , . Buradan
Cevap. .
Evrensel trigonometrik ikame
formun trigonometrik denklemi
Nerede --- rasyonel formüllerin yardımıyla fonksiyon -- ve formüllerin yardımıyla -- bağımsız değişkenlere göre rasyonel bir denkleme indirgenebilir , , , ardından denklem şuna göre cebirsel bir rasyonel denkleme indirgenebilir evrensel trigonometrik ikame formüllerini kullanarak
Formüllerin kullanılması, noktalarda tanımlanmadığından orijinal denklemin ODZ'sinin daralmasına yol açabileceğine dikkat edilmelidir, bu nedenle bu gibi durumlarda açıların orijinal denklemin kökleri olup olmadığını kontrol etmek gerekir. .
Örnek Denklemi çözün.
Çözüm. Göreve göre. Formülleri uygulayarak ve yerine koyarak, elde ederiz
nereden ve bu nedenle, .
formun denklemleri
Formun denklemleri, burada --- polinom, bilinmeyenler değiştirilerek çözülür
Örnek Denklemi çözün.
Çözüm.İkameyi yapmak ve bunu dikkate alarak,
Neresi , . --- yabancı kök, çünkü . Denklem kökleri 
.
Sınırlı İşlevlerin Kullanımı
Merkezi test uygulamasında, çözümü fonksiyonların sınırlılığına dayanan denklemlerle karşılaşmak alışılmadık bir durum değildir ve . Örneğin:
Örnek Denklemi çözün.
Çözüm., olduğundan, sol taraf , değerini aşmaz ve eşittir.
Her iki denklemi de sağlayan değerleri bulmak için aşağıdaki gibi ilerliyoruz. Bunlardan birini çözüyoruz, sonra bulunan değerler arasından diğerini tatmin edenleri seçiyoruz.
İkinci ile başlayalım: , . Daha sonra , 
.
Sadece çift sayılar için olacağı açıktır.
Cevap. .
Başka bir fikir, aşağıdaki denklemi çözerek gerçekleştirilir:
Örnek
denklemi çözün 
.
Çözüm.Üstel fonksiyonun özelliğini kullanalım: , 
.
Bu eşitsizlikleri terim terim ekleyerek şunu elde ederiz:
Bu nedenle, bu denklemin sol tarafı, ancak ve ancak iki eşitlik sağlandığında eşittir:
yani , , değerlerini alabilir veya , değerlerini alabilir.
Cevap. , .
Örnek
denklemi çözün 
.
Çözüm., . Buradan, 
.
Cevap. .
Örnek denklemi çözün
Çözüm. Gösterin , sonra sahip olduğumuz ters trigonometrik fonksiyonun tanımından 
Ve 
.
olduğundan, eşitsizlik denklemden gelir, yani. . beri ve , o zaman ve . Ancak ve bu nedenle.
ve ise, o zaman . Daha önce kurulduğundan beri , o zaman .
Cevap. , .
Örnek denklemi çözün
Çözüm. Denklemin geçerli değerlerinin aralığı .
Önce fonksiyonun olduğunu gösterelim.
Herhangi biri için yalnızca pozitif değerler alabilir.
Fonksiyonu aşağıdaki gibi gösterelim: .
O zamandan beri , yani, 
.
Bu nedenle, eşitsizliği kanıtlamak için şunu göstermek gerekir: 
. Bu amaçla, bu eşitsizliğin her iki tarafının da küpünü alırız, sonra
Ortaya çıkan sayısal eşitsizlik şunu gösterir. Bunu da hesaba katarsak, denklemin sol tarafı negatif değildir.
Şimdi denklemin sağ tarafını ele alalım.
Çünkü 
, O
Ancak, bilinmektedir ki 
. Buradan şu sonuç çıkıyor, yani. denklemin sağ tarafı geçmez. Daha önce, denklemin sol tarafının negatif olmadığı kanıtlandı, bu nedenle, eşitlik ancak her iki parçasının da eşit olduğu durumda olabilir ve bu yalnızca için mümkündür.
Cevap. .
Örnek denklemi çözün
Çözüm. belirtmek ve 
. Cauchy-Bunyakovsky eşitsizliğini uygulayarak elde ederiz. Dolayısıyla bunu takip eder 
. Öte yandan, var 
. Bu nedenle, denklemin kökleri yoktur.
Cevap. .
Örnek Denklemi çözün:
Çözüm. Denklemi şu şekilde yeniden yazalım:
Cevap. .
Trigonometrik ve birleşik denklemleri çözmek için fonksiyonel yöntemler
Dönüşümlerin bir sonucu olarak her denklem, belirli bir çözüm yöntemi olan şu veya bu standart formun bir denklemine indirgenemez. Bu gibi durumlarda, fonksiyonların bu tür özelliklerini ve monotonluk, sınırlılık, düzgünlük, periyodiklik vb. bu aralıktaki bir kök, bu kök benzersizdir ve örneğin seçimle bulunabilir. Fonksiyon yukarıdan sınırlandırılmışsa ve , ve fonksiyon aşağıdan sınırlandırılmışsa ve , o zaman denklem denklem sistemine eşdeğerdir
Örnek denklemi çözün
Çözüm. Orijinal denklemi forma dönüştürüyoruz
ve 'ye göre bir kare olarak çözün. Sonra alırız
İlk küme denklemini çözelim. Fonksiyonun sınırlılığını dikkate alarak, denklemin sadece aralıkta bir kökü olabileceği sonucuna varıyoruz. Bu aralıkta fonksiyon artar ve fonksiyon 
azalır. Bu nedenle, eğer bu denklemin bir kökü varsa, o zaman benzersizdir. Seçerek buluyoruz.
Cevap. .
Örnek denklemi çözün
Çözüm. izin ver ve 
, o zaman orijinal denklem fonksiyonel bir denklem olarak yazılabilir . İşlev tek olduğundan, o zaman . Bu durumda denklemi elde ederiz.
, ve monoton olduğundan, denklem denkleme eşdeğerdir, yani 
, tek bir kökü olan .
Cevap. .
Örnek
denklemi çözün 
.
Çözüm. türev teoremine göre karmaşık fonksiyon işlevi olduğu açıktır 
azalan (fonksiyon azalan, artan, azalan). Buradan da anlaşılacağı üzere, fonksiyon 
üzerinde tanımlı, azalan. Bu nedenle, bu denklemin en fazla bir kökü vardır. Çünkü 
, O
Cevap. .
Örnek Denklemi çözün.
Çözüm. Denklemi üç aralıkta düşünün.
a) bırak . O zaman bu kümede orijinal denklem denkleme eşdeğerdir. Aralıkta çözümü olmayan, çünkü 
, , A . Aralıkta, orijinal denklemin de kökleri yoktur, çünkü 
, A .
b) bırak . O zaman bu kümede orijinal denklem denkleme eşdeğerdir.
aralıktaki kökleri , , , sayılarıdır.
c) bırak . O zaman bu kümede orijinal denklem denkleme eşdeğerdir.
Hangi aralıkta çözümü yoktur, çünkü , ancak . Denklemin aralıkta da çözümü yoktur, çünkü , , A .
Cevap. , , , .
simetri yöntemi
Görev bildirimi bir denklemin, eşitsizliğin, sistemin vb. çözümünün benzersiz olması gerekliliğini içerdiğinde simetri yöntemini kullanmak uygundur. veya çözüm sayısının kesin bir göstergesi. Bu durumda, verilen ifadelerin herhangi bir simetrisi tespit edilmelidir.
Farklı olası simetri türlerinin çeşitliliğini de hesaba katmak gerekir.
Aynı derecede önemli olan, simetri ile akıl yürütmede mantıksal aşamaların katı bir şekilde gözetilmesidir.
Genellikle simetri yalnızca ayarlamanıza izin verir. gerekli koşullar, ardından yeterliliklerinin kontrol edilmesi gerekmektedir.
Örnek Denklemin benzersiz bir çözümü olduğu parametrenin tüm değerlerini bulun.
Çözüm.Şuna dikkat edin ve --- çift fonksiyonlar, yani denklemin sol tarafı bir çift fonksiyondur.
Yani eğer --- çözüm denklemler, bu aynı zamanda denklemin çözümüdür. Eğer --- Sadece bir şey denklemin çözümü, o zaman gerekli , .
hadi seçelim olası denklemin kökü olmasını gerektiren değerler.
Diğer değerlerin sorunun durumunu karşılayamayacağını hemen not ediyoruz.
Ancak seçilenlerin tamamının problemin koşulunu sağlayıp sağlamadığı henüz bilinmiyor.
Yeterlilik
1) , denklem şeklini alacak 
.
2) , denklem şu şekli alacaktır:
Açıkçası, herkes için ve 
. Bu nedenle, son denklem sisteme eşdeğerdir:
Böylece, için denklemin tek bir çözümü olduğunu kanıtladık.
Cevap. .
Fonksiyon keşfi ile çözüm
Örnek Denklemin tüm çözümlerinin olduğunu kanıtlayın
Bütün sayılar.
Çözüm. Orijinal denklemin ana periyodu . Bu nedenle, önce bu denklemi segment üzerinde inceliyoruz.
Denklemi forma dönüştürelim:
Bir hesap makinesinin yardımıyla şunu elde ederiz:
Eğer , o zaman önceki eşitliklerden şunu elde ederiz:
Ortaya çıkan denklemi çözerek şunu elde ederiz: .
Yapılan hesaplamalar, aralığa ait denklemin köklerinin ve olduğunu varsayma olanağı sağlar.
Doğrudan doğrulama bu hipotezi doğrular. Böylece, denklemin köklerinin sadece , tamsayı olduğu kanıtlanmıştır.
Örnek
Denklemi çözün 
.
Çözüm. Denklemin ana periyodunu bulun. Fonksiyonun ana periyodu . Fonksiyonun ana periyodu . Sayıların en küçük ortak katı ve eşittir. Bu nedenle, denklemin ana periyodu . İzin vermek .
Açıktır ki, denklemin bir çözümüdür. Aralıkta. Fonksiyon negatiftir. Bu nedenle, denklemin diğer kökleri yalnızca x ve .
Bir mikro hesap makinesi yardımıyla önce denklemin köklerinin yaklaşık değerlerini buluyoruz. Bunu yapmak için, bir fonksiyon değerleri tablosu derliyoruz. 
aralıklarla ve ; yani, aralıklarda ve .
| 0 | 0 | 202,5 | 0,85355342 |
| 3 | -0,00080306 | 207 | 0,6893642 |
| 6 | -0,00119426 | 210 | 0,57635189 |
| 9 | -0,00261932 | 213 | 0,4614465 |
| 12 | -0,00448897 | 216 | 0,34549155 |
| 15 | -0,00667995 | 219 | 0,22934931 |
| 18 | -0,00903692 | 222 | 0,1138931 |
| 21 | -0,01137519 | 225 | 0,00000002 |
| 24 | -0,01312438 | 228 | -0,11145712 |
| 27 | -0,01512438 | 231 | -0,21961736 |
| 30 | -0,01604446 | 234 | -0,32363903 |
| 33 | -0,01597149 | 237 | -0,42270819 |
| 36 | -0,01462203 | 240 | -0,5160445 |
| 39 | -0,01170562 | 243 | -0,60290965 |
| 42 | -0,00692866 | 246 | -0,65261345 |
| 45 | 0,00000002 | 249 | -0,75452006 |
| 48 | 0,00936458 | 252 | -0,81805397 |
| 51 | 0,02143757 | 255 | -0,87270535 |
| 54 | 0,03647455 | 258 | -0,91803444 |
| 57 | 0,0547098 | 261 | -0,95367586 |
| 60 | 0,07635185 | 264 | -0,97934187 |
| 63 | 0,10157893 | 267 | -0,99482505 |
| 66 | 0,1305352 | 270 | -1 |
| 67,5 | 0,14644661 |
Aşağıdaki hipotezler tablodan kolayca görülmektedir: Segmente ait denklemin kökleri sayılardır: ; ; . Doğrudan doğrulama bu hipotezi doğrular.
Cevap.
; 
; .
Birim çemberi kullanarak trigonometrik eşitsizlikleri çözme
Trigonometrik fonksiyonlardan biri olan formun trigonometrik eşitsizliklerini çözerken, eşitsizliğin çözümünü en açık şekilde sunmak ve cevabı yazmak için bir trigonometrik daire kullanmak uygundur. Trigonometrik eşitsizlikleri çözmenin ana yöntemi, onları türün en basit eşitsizliklerine indirgemektir. Bu tür eşitsizliklerin nasıl çözüleceğine dair bir örneğe bakalım.
Örnek Eşitsizliği çöz.
Çözüm. Bir trigonometrik daire çizelim ve üzerinde ordinatın 'den büyük olduğu noktaları işaretleyelim.
Bu eşitsizliğin çözümü için . Ayrıca, eğer bir sayı belirtilen aralıktan bir sayıdan farklıysa, o zaman da daha az olmayacağı da açıktır. Bu nedenle, çözümün bulunan bölümünün sonuna eklemeniz yeterlidir. Son olarak, orijinal eşitsizliğin çözümlerinin hepsinin olacağını anlıyoruz. 
.
Cevap.
.
Teğet ve kotanjant ile eşitsizlikleri çözmek için teğet ve kotanjantlardan oluşan bir çizgi kavramı yararlıdır. Bunlar sırasıyla (şekil (1) ve (2)'de) trigonometrik daireye değen çizgilerdir.
Orijini orijinde olan bir ışın oluşturursanız, apsis ekseninin pozitif yönü ile bir açı yaparak, o zaman parçanın bu ışının çizgiyle kesiştiği noktaya kadar olan uzunluğunun olduğunu görmek kolaydır. tanjantlar, bu ışının apsis ekseni ile yaptığı açının tanjantına tam olarak eşittir. Benzer bir gözlem kotanjant için de geçerlidir.
Örnek Eşitsizliği çöz.
Çözüm. Gösterin, o zaman eşitsizlik en basit şeklini alacaktır: . Teğetin en küçük pozitif periyoduna (LPP) eşit uzunlukta bir aralık düşünün. Bu doğru parçasında, teğet doğrusunu kullanarak şunu kuruyoruz. Şimdi fonksiyonun RPE'sinden beri eklenmesi gerekenleri hatırlıyoruz. Bu yüzden, 
. Değişkene dönersek, bunu elde ederiz.
Cevap.
.
Ters trigonometrik fonksiyonların grafiklerini kullanarak ters trigonometrik fonksiyonlarla eşitsizlikleri çözmek uygundur. Bunun nasıl yapıldığını bir örnekle gösterelim.
Trigonometrik eşitsizlikleri grafik yöntemle çözme
not eğer --- periyodik Bu durumda, eşitsizliği çözmek için, uzunlukları fonksiyonun periyoduna eşit olan bir doğru parçası üzerinde çözümlerini bulmak gerekir. Orijinal eşitsizliğin tüm çözümleri, bulunan değerlerden ve ayrıca işlevin herhangi bir tamsayı periyodu tarafından bulunanlardan farklı olanlardan oluşacaktır.
Eşitsizliğin çözümünü düşünün ().
O zamandan beri, eşitsizliğin için bir çözümü yoktur. Eğer , o zaman eşitsizliğin çözüm kümesi --- bir demet tüm gerçek sayılar.
İzin vermek . Sinüs işlevi en küçük pozitif periyoda sahiptir, bu nedenle eşitsizlik önce bir uzunluk parçasında, örneğin bir parçada çözülebilir. Fonksiyonların ve () grafiklerini oluşturuyoruz. formun eşitsizlikleri tarafından verilir: ve, nereden,
Bu yazıda, trigonometrik denklemleri ve eşitsizlikleri çözmek için hem en basit hem de Olimpiyat seviyesindeki yöntemler ele alınmıştır. Trigonometrik denklemleri ve eşitsizlikleri çözmenin ana yöntemleri, ayrıca, spesifik olarak kabul edildi. --- karakteristik sadece trigonometrik denklemler ve eşitsizlikler için --- ve trigonometrik denklemlere uygulanan denklemleri ve eşitsizlikleri çözmek için genel fonksiyonel yöntemler.
Tez, temel teorik bilgiler sağlar: trigonometrik ve ters trigonometrik fonksiyonların tanımı ve özellikleri; trigonometrik ifadelerin dönüştürülmesi için çok önemli olan trigonometrik fonksiyonların diğer trigonometrik fonksiyonlar cinsinden ifadesi, özellikle ters trigonometrik fonksiyonları içerenler; okul dersinden iyi bilinen temel trigonometrik formüllere ek olarak, ters trigonometrik fonksiyonları içeren ifadeleri basitleştiren formüller verilir. Temel trigonometrik denklemlerin çözümü, faktoring yöntemi, trigonometrik denklemleri cebirsel denklemlere indirgeme yöntemleri ele alınır. Trigonometrik denklemlerin çözümlerinin birkaç şekilde yazılabileceği ve bu çözümlerin şeklinin bu çözümlerin aynı mı yoksa farklı mı olduğunu hemen belirlemeye izin vermediği gerçeği göz önüne alındığında, trigonometrik denklemleri çözmek için genel bir şema ele alınır ve trigonometrik denklemlerin genel çözüm gruplarının dönüşümü ayrıntılı olarak ele alınmıştır. Temel trigonometrik eşitsizlikleri hem birim çember üzerinde hem de grafik yöntemle çözme yöntemleri ayrıntılı olarak ele alınmıştır. Temel olmayan trigonometrik eşitsizlikleri temel eşitsizlikler yoluyla çözme süreci ve okul çocukları tarafından zaten iyi bilinen aralıklar yöntemi açıklanmaktadır. Kök seçimi için tipik görevlerin çözümleri verilmiştir. Köklerin seçimi için gerekli teorik bilgiler verilir: tamsayılar kümesinin kesişmeyen alt kümelere bölünmesi, tamsayılarda denklemlerin çözümü (diophantine).
Bu tez çalışmasının sonuçları, dönem ödevlerinin ve tezlerin hazırlanmasında, okul çocukları için seçmeli derslerin hazırlanmasında eğitim materyali olarak kullanılabilir ve çalışma, öğrencileri giriş sınavlarına ve merkezi sınavlara hazırlamada da kullanılabilir.
Vygodsky Ya.Ya., Temel matematik el kitabı. /Vygodsky Ya.Ya. --- M.: Nauka, 1970.
İgudisman O., Sözlü sınavda matematik / İgudisman O. --- M .: İris matbaası, Rolf, 2001.
Azarov A.I., denklemler / Azarov A.I., Gladun O.M., Fedosenko V.S. --- Minsk: Trivium, 1994.
Litvinenko V.N., Temel matematik atölyesi / Litvinenko V.N. --- M .: Eğitim, 1991.
Sharygin I.F., Seçmeli matematik dersi: problem çözme / Sharygin I.F., Golubev V.I. --- M.: Aydınlanma, 1991.
Bardushkin V., Trigonometrik denklemler. Kök seçimi / V. Bardushkin, A. Prokofiev.// Matematik, No. 12, 2005 s. 23--27.
Vasilevsky A.B., Matematikte ders dışı çalışma için ödevler / Vasilevsky A.B. --- Mn.: Halkın Asveta'sı. 1988. --- 176'lar.
Sapunov P. I., Trigonometrik denklemlerin genel çözüm gruplarının dönüşümü ve birliği / Sapunov P. I. // Matematik eğitimi, sayı No. 3, 1935.
Borodin P., Trigonometri. Moskova Devlet Üniversitesi'ndeki giriş sınavlarının materyalleri [metin] / P. Borodin, V. Galkin, V. Panferov, I. Sergeev, V. Tarasov // Matematik No. 1, 2005 s. 36--48.
Samusenko A.V., Matematik: Başvuru sahiplerinin tipik hataları: Referans el kitabı / Samusenko A.V., Kazachenok V.V. --- Minsk: Yüksek Okul, 1991.
Azarov A.I., Sınav problemlerini çözmek için fonksiyonel ve grafiksel yöntemler / Azarov A.I., Barvenov S.A., --- Minsk: Aversev, 2004.
TANIM
Trigonometrik eşitsizlikler, bir trigonometrik fonksiyonun işareti altında bir değişken içeren eşitsizliklerdir.
Trigonometrik eşitsizlikleri çözme
Trigonometrik eşitsizliklerin çözümü genellikle şu formun en basit trigonometrik eşitsizliklerini çözmeye gelir: \(\ \sin x a \), \(\ \cos x > a \), \(\ \operatorname(tg) x > a \ ), \(\ \ operatöradı(ctg) x > a \), \(\ \sin x \leq a \), \(\ \cos x \leq a \), \(\ \operatöradı(tg) x \ leq a \), \ (\ \operatöradı(ctg) x \leq a \), \(\ \sin x \geq a \), \(\ \cos \geq a \), \(\ \operatöradı(tg) ) x \geq a \ ), \(\ \operatöradı(tg) x \geq a \)
En basit trigonometrik eşitsizlikler grafik olarak veya bir birim trigonometrik daire kullanılarak çözülür.
Tanım gereği, \(\ \alpha \) açısının sinüsü, birim çemberin \(\ P_(\alpha)(x, y) \) noktasının ordinatıdır (Şekil 1) ve kosinüs, bu noktanın apsisi. Bu gerçek, birim çemberi kullanarak kosinüs ve sinüs ile en basit trigonometrik eşitsizlikleri çözmede kullanılır.
Trigonometrik eşitsizlikleri çözme örnekleri
\(\ \sin x \leq \frac(\sqrt(3))(2) \) eşitsizliğini çözün
\(\ \left|\frac(\sqrt(3))(2)\right| olduğundan, bu eşitsizliğin bir çözümü vardır ve iki şekilde çözülebilir.
İlk yol. Bu eşitsizliği grafiksel olarak çözelim. Bunu yapmak için, aynı koordinat sisteminde sinüs \(\ y=\sin x \) (Şekil 2) ve düz çizgi \(\ y=\frac(\sqrt(3))( 2) \)
\(\ y=\frac(\sqrt(3))(2) \) doğrusunun grafiğinin altında sinüsoidin bulunduğu aralıkları seçelim. Bu grafiklerin kesişme noktalarının \(\ x_(1) \) ve \(\ x_(2) \) apsislerini bulun: \(\ x_(1)=\pi-\arcsin \frac(\sqrt(3) )(2 )=\pi-\frac(\pi)(3)=\frac(2 \pi)(3) x_(2)=\arcsin \frac(\sqrt(3))(2)+2 \pi=\ frac(\pi)(3)+2 \pi=\frac(7 \pi)(3) \)
\(\ \left[-\frac(4 \pi)(3) ; \frac(\pi)(3)\right] \) aralığını elde ettik, ancak \(\ y=\sin x \) işlevi periyodiktir ve bir periyodu vardır \(\ 2 \pi \) , o zaman cevap aralıkların birleşimidir: \(\ \left[\frac(2 \pi)(3)+2 \pi k ; \frac(7) \pi)(3)+ 2 \pi k\right] \), \(\ k \in Z \)
İkinci yol. Bir birim çember ve bir doğru \(\ y=\frac(\sqrt(3))(2) \) oluşturun, kesişme noktalarını \(\ P_(x_(1)) \) ve \(\ P_(x_) belirtin (2 )) \) (Şek. 3). Orijinal eşitsizliğin çözümü, \(\ \frac(\sqrt(3))(2) \) değerinden küçük olan ordinat noktaları kümesi olacaktır. Saat yönünün tersine giderek \(\ \boldsymbol(I)_(1) \) ve \(\ \boldsymbol(I)_(2) \) değerini bulalım, \(\ x_(1) Şekil 3
\(\ x_(1)=\pi-\arcsin \frac(\sqrt(3))(2)=\pi-\frac(\pi)(3)=\frac(2 \pi)(3) x_ (2)=\arcsin \frac(\sqrt(3))(2)+2 \pi=\frac(\pi)(3)+2 \pi=\frac(7 \pi)(3) \)
Sinüs fonksiyonunun periyodikliğini hesaba katarak, sonunda \(\ \left[\frac(2 \pi)(3)+2 \pi k ; \frac(7 \pi)(3)+2 \) aralıklarını elde ederiz. pi\sağ] \), \(\k\in Z\)
\(\ \sin x>2 \) eşitsizliğini çözün
Sinüs sınırlı bir fonksiyondur: \(\ |\sin x| \leq 1 \) ve bu eşitsizliğin sağ tarafı birden büyüktür, dolayısıyla çözüm yoktur.
\(\ \cos x>\frac(1)(2) \) eşitsizliğini çözün
Bu eşitsizlik iki şekilde çözülebilir: grafiksel olarak ve birim çember kullanılarak. Yöntemlerin her birini ele alalım.
İlk yol. Eşitsizliğin sağ ve sol kısımlarını yani \(\ y=\cos x \) ve \(\ y=\frac(1)(2) \) fonksiyonlarını tek bir koordinat sisteminde gösterelim. Kosinüs fonksiyonu \(\ y=\cos x \) grafiğinin \(\ y=\frac(1)(2) \) doğrusunun grafiğinin üzerinde olduğu aralıkları seçelim (Şekil 4) ).
\(\ \boldsymbol(x)_(1) \) ve \(\ x_(2) \) noktalarının apsislerini bulun - \(\ y=\cos x \) fonksiyonlarının grafiklerinin kesişme noktaları ) ve \(\ y=\frac (1)(2) \) , belirtilen eşitsizliğin tutulduğu aralıklardan birinin uçlarıdır. \(\ x_(1)=-\arccos \frac(1)(2)=-\frac(\pi)(3) \); \(\ x_(1)=\arccos \frac(1)(2)=\frac(\pi)(3) \)
Kosinüsün periyodu \(\ 2 \pi \) olan periyodik bir fonksiyon olduğu düşünülürse, cevap \(\ \left(-\frac(\pi)(3) aralıklarından \(\ x \) değeridir. )+2 \pi k ; \frac(\pi)(3)+2 \pi k\right) \), \(\ k \in Z \)
İkinci yol. Bir birim çember ve bir doğru \(\ x=\frac(1)(2) \) çizelim (çünkü x ekseni birim çemberdeki kosinüslere karşılık gelir). \(\ P_(x_(1)) \) ve \(\ P_(x_(2)) \) (Şekil 5) doğru ile birim çemberin kesişme noktaları olsun. Orijinal denklemin çözümü, \(\ \frac(1)(2) \) 'den küçük olan apsis noktaları kümesi olacaktır. \(\ x_(1) \) ve \(\ 2 \) değerlerini saat yönünün tersine çevirerek bulun, böylece \(\ x_(1) Kosinüsün periyodikliğini hesaba katarak, sonunda \( \ \left(-\frac (\pi)(3)+2 \pi k ;\frac(\pi)(3)+2 \pi k\right) \),\(\ k \in Z \)
\(\ \operatorname(ctg) x \leq-\frac(\sqrt(3))(3) \) eşitsizliğini çözün
Tek bir koordinat sisteminde \(\ y=\operatöradı(ctg) x \), \(\ y=-\frac(\sqrt(3))(3) \) fonksiyonlarının grafiklerini çizelim
\(\ y=\operatöradı(ctg) x \) fonksiyonunun grafiğinin \(\ y=-\frac(\sqrt(3))( 3) \) (Şek. 6) .
Eşitsizliğin \(\ x_(0)=\operatorname(arcctg)\left(-\frac(\) olduğu aralıklardan birinin sonu olan \(\ x_(0) \) noktasının apsisini bulun sqrt(3)( 3)\sağ)=\pi-\operatöradı(arcctg)\left(\frac(\sqrt(3))(3)\sağ)=\pi-\frac(\pi)(3 )=\frac(2 \pi)(3) \)
Bu boşluğun diğer ucu \(\ \pi \) noktasıdır ve \(\ y=\operatöradı(ctg) x \) işlevi bu noktada tanımsızdır. Dolayısıyla, bu eşitsizliğin çözümlerinden biri \(\ \frac(2 \pi)(3) \leq x aralığıdır.
ile trigonometrik eşitsizlikler karmaşık argüman
Karmaşık bir argümana sahip trigonometrik eşitsizlikler, bir ikame kullanılarak en basit trigonometrik eşitsizliklere indirgenebilir. Çözdükten sonra ters yerine koyma yapılır ve asıl bilinmeyen ifade edilir.
\(\ 2 \cos \left(2 x+100^(\circ)\right) \leq-1 \) eşitsizliğini çözün
Bu eşitsizliğin sağ tarafındaki kosinüsü ifade edin: \(\ \cos \left(2 x+100^(\circ)\right) \leq-\frac(1)(2) \)
\(\ t=2 x+100^(\circ) \) değiştirmesini gerçekleştiriyoruz, ardından bu eşitsizlik en basit eşitsizliğe dönüştürülüyor \(\ \cos t \leq-\frac(1)(2) \ )
birim çemberi kullanarak çözelim. Bir birim çember ve bir doğru \(\ x=-\frac(1)(2) \) çizelim. \(\ P_(1) \) ve \(\ P_(2) \) doğru ile birim çemberin kesişme noktaları olarak gösterelim (Şekil 7).
Orijinal eşitsizliğin çözümü, en çok \(\ -\frac(1)(2) \) olan apsis noktaları kümesi olacaktır. \(\ P_(1) \) noktası, \(\ 120^(\circ) \) açısına ve \(\ P_(2) \) noktasına karşılık gelir. Böylece, kosinüs periyodu verildiğinde, \(\ 120^(\circ)+360^(\circ) \cdot n \leq t \leq 240^(\circ)+360^(\circ) \cdot n \ elde ederiz. ) , \(\ n \in Z \)
Ters ikame \(\ t=2 x+100^(\circ) 120^(\circ)+360^(\circ) \cdot n \leq 2 x+100^(\circ) \leq 240^ yapıyoruz (\ circ)+360^(\circ) \cdot n \), \(\ n \in Z \)
\(\ \mathbf(x) \) ifade ediyoruz, bunun için önce \(\ 100^(\circ) 120^(\circ)-100^(\circ)+360^(\circ) \ cdot'u çıkarın n \leq 2 x+100^(\circ)-100^(\circ) \leq 240^(\circ)-100^(\circ)+360^(\circ) \cdot n \), \( \ n\in Z\); \(\ 20^(\circ)+360^(\circ) \cdot n \leq 2 x \leq 140^(\circ)+360^(\circ) \cdot n \), \(\ n \in Z\)
ve sonra 2 \(\ \frac(20^(\circ)+360^(\circ) \cdot n)(2) \leq \frac(2 x)(2) \leq \frac(140^) ile bölün (\circ)+360^(\circ) \cdot n)(2) \), \(\ n \in Z \); \(\ 10^(\circ)+180^(\circ) \cdot n \leq x \leq 70^(\circ)+180^(\circ) \cdot n \), \(\ n \in Z \)
Çift trigonometrik eşitsizlikler
Çift trigonometrik eşitsizliği çözün \(\ \frac(1)(2)
\(\ t=\frac(x)(2) \) yerine koymayı tanıtalım, ardından orijinal eşitsizlik \(\ \frac(1)(2) şeklini alacaktır.
birim çemberi kullanarak çözelim. Birim çember üzerinde ordinat ekseni sinüse karşılık geldiği için, üzerinde \(\ x=\frac(1)(2) \)'den büyük ve \(\'den küçük veya eşit olan koordinatlar kümesini seçiyoruz. \frac(\sqrt(2)(2 ) \) . Şekil 8'de bu noktalar \(\ P_(t_(1)) \), \(\ P_(t_(2)) \) ve \(\ P_(t_(3)) \) yayları üzerinde yer alacaktır. , \( \ P_(t_(4)) \) . Saat yönünün tersine tur yaparak \(\ t_(1) \), \(\ t_(2) \), \(\ t_(3) \), \(\ t_(4) \) değerini bulalım ve \ (\ t_(1) \(\ t_(3)=\pi-\arcsin \frac(\sqrt(2))(2)=\pi-\frac(\pi)(4)=\frac(3) \ pi)(4) \); \(\ t_(4)=\pi-\arcsin \frac(1)(2)=\pi-\frac(\pi)(6)=\frac(5 \pi ) (6)\)
Böylece sinüs fonksiyonunun periyodikliği dikkate alınarak aşağıdaki gibi yazılabilen iki aralık elde ederiz \(\ \frac(\pi)(6)+2 \pi k \leq t \frac(\pi) (4)+2 \ pi k \quad \frac(3 \pi)(4)+2 \pi k leq \frac(x)(2) \frac(\pi)(4)+2 \pi k \) , \(\ \frac(3 \pi)(4)+2 \pi k Express \(\ \mathbf( x) \), bunun için her iki eşitsizliğin her tarafını 2 ile çarparsak \(\ \frac (\pi)(3)+4 \pi k \leq x