Привіт! Ми вже знаємо, що такий розподіл імовірностей. Воно може бути дискретним чи безперервним, і ми довідалися, що його називають щільністю розподілу ймовірностей. Тепер давайте вивчимо кілька найбільш поширених розподілів. Припустимо, у мене є монета, причому правильна монета, і я збираюся підкинути її 5 разів. Також я визначу випадкову величину Х, позначу її великою літерою X, вона дорівнюватиме кількості «орлів» при 5 підкиданнях. Може, у мене є 5 монет, я підкину їх усі одразу і порахую, скільки у мене випало «орлів». Або в мене могла бути одна монета, я могла б її підкинути 5 разів і порахувати, скільки разів у мене випав «орел». Це, власне, не має значення. Але припустимо, що в мене одна монета, і я підкину її 5 разів. Тоді ми не матимемо невизначеності. Отже, ось визначення моєї випадкової величини. Як ми знаємо, випадкова величина трохи відрізняється від звичайної змінної, вона більше схожа на функцію. Вона надає якесь значення експерименту. І ця випадкова величина досить проста. Ми просто вважаємо, скільки разів випав «орел» після 5 підкидань – це і є наша випадкова величина X. Давайте подумаємо, які можуть бути ймовірності різних значень у нашому випадку? Так, яка ймовірність того, що Х (заголовна Х) дорівнює 0? Тобто. яка ймовірність того, що після 5 підкидань жодного разу не випаде орел? Ну, це, по суті, те саме, що ймовірність випадання одних «решічок» (це так, невеликий огляд теорії ймовірностей). У вас мають випасти одні «решки». Яка ймовірність кожної з цих «грашок»? Це 1/2. Тобто. тут має бути 1/2 помножити на 1/2, 1/2, 1/2 і знову на 1/2. Тобто. (1/2)⁵. 1⁵=1, розділити на 2⁵, тобто. на 32. Цілком логічно. Так… Я трохи повторю те, що ми проходили з теорії ймовірностей. Це важливо для того, щоб розуміти, куди ми зараз рухаємось і як, власне, формується дискретний розподіл ймовірностей. Отже, а яка ймовірність того, що в нас рівно один раз випаде орел? Ну, орел міг би випасти при першому підкиданні. Тобто. могло бути так: «орел», «решка», «решка», «решка», «решка». Або "орел" міг би випасти при другому підкиданні. Тобто. могла б бути така комбінація: «решка», «орел», «решка», «решка», «решка» тощо. Один "орел" міг би випасти після будь-якого з 5 підкидань. Якою є ймовірність кожної з цих ситуацій? Імовірність випадання "орла" дорівнює 1/2. Потім можливість випадання «решки», що дорівнює 1/2, помножити на 1/2, на 1/2, на 1/2. Тобто. ймовірність кожної з цих ситуацій дорівнює 1/32. Так само, як і можливість ситуації, де Х=0. По суті, ймовірність будь-якого особливого порядку випадень «орла» та «решки» дорівнюватиме 1/32. Отже, ймовірність цього дорівнює 1/32. І ймовірність цього дорівнює 1/32. І ось такі ситуації мають місце тому, що «орел» міг би випасти за будь-якого з 5 підкидань. Отже, ймовірність те, що точно випаде один «орел», дорівнює 5*1/32, тобто. 5/32. Цілком логічно. Тепер починається цікаве. Яка ймовірність… (писатиму кожен із прикладів іншим кольором)… яка ймовірність того, що моя випадкова величина дорівнює 2? Тобто. я підкину монету 5 разів, і якою є ймовірність того, що 2 рази точно випаде «орел»? Це вже цікавіше, правда? Які можливі комбінації? Могла б бути "орел", "орел", "решка", "решка", "решка". Також могла бути «орел», «решка», «орел», «решка», «решка». І якщо подумати, що ці два «орли» можуть стояти у різних місцях комбінації, то можна трохи заплутатися. Вже не можна думати про розміщення так, як ми це робили тут, вгорі. Хоча… можна тільки ризикуєте заплутатися. Ви маєте зрозуміти одне. Для кожної з цих комбінацій ймовірність дорівнює 1/32. ½*½*½*½*½. Тобто. ймовірність кожної з цих комбінацій дорівнює 1/32. І ми маємо подумати над тим, скільки існує таких комбінацій, що задовольняють нашій умові (2 «орли»)? Тобто. по суті, потрібно уявити, що є 5 підкидань монети, і потрібно з них вибрати 2, за яких випадає «орел». Давайте уявимо, що наші 5 підкидань зібралися в кружальце, також уявімо, що у нас є лише два стільці. І ми кажемо: «Добре, хто з вас сяде на ці стільці для орлів? Тобто. хто з вас буде орлом? І нас не цікавить те, як вони сядуть. Я наводжу такий приклад, сподіваючись, що так вам буде зрозуміліше. І може, вам захочеться подивитися деякі уроки з теорії ймовірностей на цю тему, коли я говоритиму про біном Ньютона. Тому що там я більш детально заглиблюся у все це. Але якщо ви міркуватимете таким шляхом, то зрозумієте, що таке біноміальний коефіцієнт. Бо якщо думатимете так: добре, у мене 5 підкидань, при якому підкиданні випаде перший «орел»? Ну, тут 5 можливостей того, за якого за рахунком підкидання випаде перший «орел». А скільки можливостей для другого орла? Ну, перше підкидання, яке ми вже використовували, забрало можливість випадання «орла». Тобто. одна позиція «орла» у комбінації вже зайнята одним із підкидань. Тепер залишилося 4 підкидання, отже, другий «орел» може випасти за одного з 4 підкидань. І ви це бачили, ось тут. Я вибрала так, що «орел» випав при 1-му підкиданні, і припустила, що при 1 з 4 кидків, що залишилися, також повинен випасти «орел». Отже, тут лише 4 можливості. Все, що я говорю, означає, що для першого «орла» у вас є 5 різних позицій, на які він може випасти. А для другого вже залишається лише 4 позиції. Подумайте про це. Коли ми обчислюємо так, то порядок враховується. Але для нас зараз не має значення, в якій послідовності випадають «орли» та «решки». Ми не говоримо, що це орел 1 або що це орел 2. В обох випадках це просто орел. Ми могли б припустити, що це орел 1, а це орел 2. Або могло бути навпаки: це міг би бути другий «орел», а це – «перший». І я говорю це тому, що важливо зрозуміти, де використовувати розміщення, а де – поєднання. Нас не цікавить послідовність. Тож, власне, є лише 2 способи походження нашої події. Значить, ділимо це на 2. І як ви пізніше побачите, тут 2! способів походження нашої події Якби було 3 «орла», тоді тут було б 3!, і я покажу вам чому. Отже, це буде одно… 5*4=20 і розділити на 2 – вийде 10. Тому тут 10 різних комбінацій із 32, у яких у вас точно буде 2 «орли». Отже, 10*(1/32) дорівнює 10/32, а чому це одно? 5/16. Запишу через біноміальний коефіцієнт. Це значення, ось тут, вгорі. Якщо подумати, то це – те саме, що й 5!, поділений на… Що означає ось це 5*4? 5! - Це 5 * 4 * 3 * 2 * 1. Тобто. якщо мені тут потрібно лише 5*4, то для цього я можу поділити 5! на 3! Це одно 5*4*3*2*1, поділений на 3*2*1. І залишається лише 5*4. Значить, це те саме, що і цей чисельник. І потім, т.к. нас не цікавить послідовність, нам потрібно тут 2. Власне, 2! Помножити на 1/32. Такою була б ймовірність того, що в нас випало б точно 2 «орли». Яка ймовірність того, що у нас точно 3 рази випаде орел? Тобто. ймовірність того, що Х = 3. Отже, за тією ж логікою, перший випадок випадання «орла» може мати місце за 1 з 5 підкидань. Другий випадок випадання «орла» може мати місце при 1 з 4 підкидів, що залишилися. А третій випадок випадання «орла» може мати місце при 1 з 3 підкидів, що залишилися. А скільки існує різних способів розставити 3 підкидання? Загалом, скільки є способів, щоб розставити 3 предмети на місця? Це 3! І ви можете це вирахувати або, можливо, захочете переглянути ті уроки, в яких я докладніше це пояснювала. Але якщо ви, наприклад, візьмете літери A, B і C, то є 6 способів, за допомогою яких ви їх можете розставити. Можете розглядати це як випадки випадання орлів. Тут могли бути ACB, CAB. Може бути BAC, BCA, і… Який останній варіант, який я не назвала? CBA. Є 6 способів розставити 3 різні предмети. Ми ділимо на 6, тому що не хочемо повторно зараховувати ці 6 різних способів, тому що розглядаємо їх як рівнозначні. Тут нас не цікавить, за якого за рахунком підкидання випаде «орел». 5*4*3… Це можна переписати, як 5!/2! І розділити це ще на 3! Це і є. 3! дорівнює 3*2*1. Трійки скорочуються. Це стає рівним 2. Це – рівним 1. Ще раз, 5*2, тобто. одно 10. Кожна ситуація має можливість 1/32, тому це знову одно 5/16. І це цікаво. Імовірність того, що у вас випаде 3 «орли» дорівнює ймовірності того, що у вас є 2 орли. І причина цього… Ну, є багато причин, що так вийшло. Але якщо подумати, що ймовірність того, що випаде 3 «орла» – те саме, що ймовірність випадання 2 «решічок». І ймовірність випадання 3 «решічок» має бути такою самою, як і ймовірність випадання 2-х «орлів». І добре, що значення ось так спрацьовують. Добре. Яка ймовірність того, що Х = 4? Ми можемо використовувати ту саму формулу, що використовували раніше. Це могло бути 5*4*3*2. Отже, тут запишемо 5 * 4 * 3 * 2 ... Скільки є різних способів розставити 4 предмети? Це 4! 4! - Це, по суті, ось ця частина, ось тут. Це 4*3*2*1. Так, це скорочується, залишається 5. Потім кожна комбінація має ймовірність 1/32. Тобто. це одно 5/32. І ще раз зауважте, що ймовірність того, що 4 рази випаде «орел», дорівнює ймовірності того, що 1 раз випаде «орел». І це є сенс, т.к. 4 «орла» – це те саме, що випадок випадання 1 «решки». Ви скажете: ну, і за якого ж підкидання випаде ця одна «решка»? Ага, для цього тут є 5 різних комбінацій. І кожна з них має можливість 1/32. І нарешті, яка ймовірність того, що Х = 5? Тобто. випадає "орел" 5 разів поспіль. Має бути так: «орел», «орел», «орел», «орел», «орел». Кожен із «орлів» має ймовірність 1/2. Ви їх перемножуєте та отримуєте 1/32. Можна піти іншим шляхом. Якщо всього є 32 способи, за допомогою яких ви можете отримати «орли» і «решки» у цих експериментах, це лише один із цих способів. Тут таких способів було 5 із 32. Тут – 10 із 32. Проте обчислення ми провели, а тепер готові намалювати розподіл ймовірностей. Але мій час минув. Дозвольте продовжити на наступному уроці. А якщо ви в настрої, то може намалюєте перед тим, як дивитися наступний урок? До швидкої зустрічі!
У цьому і кількох наступних нотатках ми розглянемо математичні моделі випадкових подій. Математична модель- це математичне вираз, що становить випадкову величину. Для дискретних випадкових величин цей математичний вираз відомий під назвою функція розподілу.
Якщо завдання дозволяє явно записати математичне вираз, що становить випадкову величину, можна обчислити точну ймовірність будь-якого її значення. У цьому випадку можна обчислити та перерахувати всі значення функції розподілу. У ділових, соціологічних та медичних додатках зустрічаються різноманітні розподіли випадкових величин. Одним із найкорисніших розподілів є біномне.
Біноміальний розподілвикористовується для моделювання ситуацій, що характеризуються такими особливостями.
- Вибірка складається з фіксованого числа елементів n, що є результатами якогось випробування.
- Кожен елемент вибірки належить одній із двох взаємовиключних категорій, які вичерпують весь вибірковий простір. Як правило, ці дві категорії називають успіх та невдача.
- Ймовірність успіху рє постійною. Отже, ймовірність невдачі дорівнює 1 – р.
- Вихід (тобто удача чи невдача) будь-якого випробування залежить від результату іншого випробування. Щоб гарантувати незалежність результатів, елементи вибірки зазвичай отримують за допомогою двох різних методів. Кожен елемент вибірки випадково витягується з нескінченної генеральної сукупності без повернення або з кінцевої генеральної сукупності з поверненням.
Завантажити нотатку у форматі або , приклади у форматі
Біноміальний розподіл використовується для оцінки кількості успіхів у вибірці, що складається з nспостережень. Розглянемо як приклад оформлення замовлень. Щоб зробити замовлення, клієнти компанії Saxon Company можуть скористатися інтерактивною електронною формою і надіслати її в компанію. Потім інформаційна система перевіряє, чи немає у замовленнях помилок, а також неповної чи недостовірної інформації. Будь-яке замовлення, що викликає сумніви, позначається та включається до щоденного звіту про виняткові ситуації. Дані, зібрані компанією, свідчать, що ймовірність помилок у замовленнях дорівнює 0,1. Компанія хотіла б знати, яка ймовірність виявити певну кількість помилкових замовлень у заданій вибірці. Наприклад, припустимо, що клієнти заповнили чотири електронних форм. Яка ймовірність, що всі замовлення виявляться безпомилковими? Як визначити цю можливість? Під успіхом розумітимемо помилку при заповненні форми, а всі інші результати вважатимемо невдачею. Нагадаємо, що нас цікавить кількість помилкових замовлень у заданій вибірці.
Які результати ми можемо спостерігати? Якщо вибірка складається з чотирьох замовлень, помилковими можуть бути одне, два, три чи всі чотири, крім того, всі вони можуть виявитися правильно заповненими. Чи може випадкова величина, що описує кількість неправильно заповнених форм, набувати будь-якого іншого значення? Це неможливо, оскільки кількість неправильно заповнених форм не може перевищувати обсяг вибірки nчи бути негативним. Таким чином, випадкова величина, що підпорядковується біноміальному закону розподілу, набуває значення від 0 до n.
Припустимо, що у вибірці із чотирьох замовлень спостерігаються такі результати:
Яка ймовірність виявити три помилкові замовлення у вибірці, що складається з чотирьох замовлень, причому у зазначеній послідовності? Оскільки попередні дослідження показали, що ймовірність помилки при заповненні форми дорівнює 0,10, ймовірності зазначених вище результатів обчислюються таким чином:
Оскільки результати не залежать один від одного, ймовірність зазначеної послідовності результатів дорівнює: р * р * (1-р) * р = 0,1 * 0,1 * 0,9 * 0,1 = 0,0009. Якщо необхідно обчислити кількість варіантів вибору X nелементів, слід скористатися формулою поєднань (1):

де n! = n * (n -1) * (n - 2) * ... * 2 * 1 - факторіал числа n, причому 0! = 1 та 1! = 1 за визначенням.
Цей вираз часто позначають як . Таким чином, якщо n = 4 і X = 3, кількість послідовностей, що складаються з трьох елементів, вилучених з вибірки, обсяг якої дорівнює 4, визначається за такою формулою:
Отже, ймовірність виявити три помилкові замовлення обчислюється так:
(Кількість можливих послідовностей) *
(ймовірність конкретної послідовності) = 4*0,0009 = 0,0036
Аналогічно можна обчислити ймовірність того, що серед чотирьох замовлень виявляться одне або два помилкові, а також ймовірність того, що всі замовлення помилкові або всі вірні. Однак при збільшенні обсягу вибірки nвизначити ймовірність конкретної послідовності результатів стає складніше. У цьому випадку слід застосувати відповідну математичну модель, яка описує біномний розподіл кількості варіантів вибору Xоб'єктів з вибірки, що містить nелементів.
Біномінальний розподіл

де Р(Х)- ймовірність Xуспіхів при заданих обсягах вибірки nта ймовірності успіху р, X = 0, 1, … n.
Зверніть увагу на те, що формула (2) є формалізацією інтуїтивних висновків. Випадкова величина X, що підпорядковується біномному розподілу, може приймати будь-яке ціле значення в діапазоні від 0 до n. Твір рX(1 – р)n – Xє ймовірність конкретної послідовності, що складається з Xуспіхів у вибірці, обсяг якої дорівнює n. Величина визначає кількість можливих комбінацій, що складаються з Xуспіхів у nвипробуваннях. Отже, при заданій кількості випробувань nта ймовірності успіху рймовірність послідовності, що складається з Xуспіхів, дорівнює
Р(Х) = (кількість можливих послідовностей) * (ймовірність конкретної послідовності) = 
Розглянемо приклади, що ілюструють застосування формули (2).
1. Припустимо, що можливість невірно заповнити форму дорівнює 0,1. Яка ймовірність того, що серед чотирьох заповнених форм три виявляться хибними? Використовуючи формулу (2), отримуємо, що ймовірність виявити три помилкові замовлення у вибірці, що складається з чотирьох замовлень, дорівнює
2. Припустимо, що можливість невірно заповнити форму дорівнює 0,1. Яка ймовірність того, що серед чотирьох заповнених форм не менше трьох виявляться хибними? Як показано в попередньому прикладі, ймовірність того, що серед чотирьох заповнених форм три виявляться помилковими, дорівнює 0,0036. Щоб обчислити ймовірність того, що серед чотирьох заповнених форм не менше трьох будуть неправильно заповнені, необхідно скласти ймовірність того, що серед чотирьох заповнених форм три виявляться помилковими, і ймовірність того, що серед чотирьох заповнених форм виявляться помилковими. Імовірність другої події дорівнює
Таким чином, ймовірність того, що серед чотирьох заповнених форм не менше трьох виявляться помилковими, дорівнює
Р(Х> 3) = Р(Х = 3) + Р(Х = 4) = 0,0036 + 0,0001 = 0,0037
3. Припустимо, що можливість невірно заповнити форму дорівнює 0,1. Яка ймовірність того, що серед чотирьох заповнених форм менше трьох виявляться хибними? Імовірність цієї події
Р(X< 3) = P(X = 0) + P(X = 1) + P(X = 2)
Використовуючи формулу (2), обчислимо кожну з цих ймовірностей:

Отже, Р(Х< 3) = 0,6561 + 0,2916 + 0,0486 = 0,9963.
Імовірність Р(Х< 3) можно вычислить иначе. Для этого воспользуемся тем, что событие X < 3 является дополнительным по отношению к событию Х>3. Тоді Р(Х< 3) = 1 – Р(Х> 3) = 1 – 0,0037 = 0,9963.
У міру збільшення обсягу вибірки nобчислення, аналогічні проведеним у прикладі 3, стають скрутними. Щоб уникати цих складнощів, багато біномних ймовірностей табулюють заздалегідь. Деякі з цих ймовірностей наведені на рис. 1. Наприклад, щоб отримати ймовірність, що Х= 2 при n= 4 та p= 0,1, слід витягти з таблиці число, яке стоїть на перетині рядка Х= 2 і стовпця р = 0,1.

Мал. 1. Біноміальна ймовірність при n = 4, Х= 2 і р = 0,1
Біноміальний розподіл можна обчислити за допомогою функції Excel = БІНОМ.РАСП() (рис. 2), що має 4 параметри: число успіхів - Х, Число випробувань (або обсяг вибірки) - n, ймовірність успіху – р, параметр інтегральна, Що приймає значення ІСТИНА (у цьому випадку обчислюється ймовірність не менше Хподій) або БРЕХНЯ (у цьому випадку обчислюється ймовірність точно Хподій).

Мал. 2. Параметри функції =БІНОМ.РАСП()
Для наведених вище трьох прикладів розрахунки наведені на рис. 3 (див. також файл Excel). У кожному стовпці наведено за однією формулою. Цифрами показано відповіді приклади відповідного номера).

Мал. 3. Розрахунок біномінального розподілу в Excel для n= 4 та p = 0,1
Властивості біномного розподілу
Біноміальний розподіл залежить від параметрів nі р. Біноміальний розподіл може бути як симетричним, так і асиметричним. Якщо р = 0,05, біномний розподіл є симетричним незалежно від величини параметра n. Однак, якщо р ≠ 0,05, розподіл стає асиметричним. Чим ближче значенняпараметра рдо 0,05 і чим більший обсяг вибірки n, Тим слабше виражена асиметрія розподілу. Таким чином, розподіл кількості неправильно заповнених форм зміщено вправо, оскільки p= 0,1 (рис. 4).

Мал. 4. Гістограма біномного розподілу при n= 4 та p = 0,1
Математичне очікування біномного розподілудорівнює добутку обсягу вибірки nна ймовірність успіху р:
(3) Μ = Е(Х) =np
У середньому, при досить довгій серії випробувань у вибірці, що складається з чотирьох замовлень, може бути р = Е(Х) = 4 х 0,1 = 0,4 неправильно заповнених форм.
Стандартне відхилення біномного розподілу
Наприклад, стандартне відхиленнякількості невірно заповнених форм у бухгалтерській інформаційної системиодно:
Використовуються матеріали книги Левін та ін. Статистика менеджерів. - М.: Вільямс, 2004. - с. 307–313
Не всі явища вимірюються в кількісній шкалі типу 1, 2, 3…100500… Не завжди явище може приймати нескінченну чи велику кількість різних станів. Наприклад, стать у людини може бути М, або Ж. Стрілець або потрапляє в ціль, або не потрапляє. Голосувати можна або "За", або "Проти" і т.д. і т.п. Інакше кажучи, такі дані відбивають стан альтернативного ознаки – або «так» (подія настала), або «ні» (подія не наступило). Подію, що настала (позитивний результат) ще називають «успіхом».
Експерименти з такими даними називаються схемою Бернуллі, на честь відомого швейцарського математика, який встановив, що при великій кількості випробувань співвідношення позитивних результатів та загальної кількості випробувань прагне ймовірності настання цієї події.
Змінна альтернативна ознака
Для того, щоб в аналізі задіяти математичний апарат, результати подібних спостережень слід записати в числовому вигляді. Для цього позитивному результату надають число 1, негативному – 0. Іншими словами, ми маємо справу зі змінною, яка може набувати лише двох значень: 0 або 1.
Яку користь звідси можна отримати? Взагалі не меншу, ніж від звичайних даних. Так, легко підрахувати кількість позитивних наслідків – досить підсумувати всі значення, тобто. всі 1 (успіхи). Можна піти далі, але для цього потрібно ввести кілька позначок.
Насамперед слід зазначити, що позитивні результати (які рівні 1) мають певну ймовірність появи. Наприклад, випадання орла при підкиданні монети дорівнює ½ або 0,5. Така ймовірність традиційно позначається латинською літерою. p. Отже, ймовірність наступу альтернативної події дорівнює 1 - p, яку ще позначають через q, тобто q = 1 - p. Зазначені позначення можна наочно систематизувати у вигляді таблички розподілу змінної X.
Ми отримали перелік можливих значень та їх ймовірності. Можна розрахувати математичне очікування і дисперсію. Матоочікування – це сума творів усіх можливих значень на відповідні їм ймовірності:
![]()
Обчислимо маточування, використовуючи позначення в таблиці вище.
Виходить, що математичне очікування альтернативної ознаки дорівнює ймовірності цієї події. p.
Тепер визначимо, що таке дисперсія альтернативної ознаки. Дисперсія є середній квадрат відхилень від математичного очікування. Загальна формула(Для дискретних даних) має вигляд:
Звідси дисперсія альтернативної ознаки:

Неважко помітити, що ця дисперсія має максимум 0,25 (при p = 0,5).
Стандартне відхилення – корінь із дисперсії:
Максимальне значення вбирається у 0,5.
Як видно, і математичне очікування, і дисперсія альтернативної ознаки мають дуже компактний вигляд.
Біноміальний розподіл випадкової величини
Розглянемо ситуацію під іншим кутом. Справді, кому цікаво, що середнє випадання орлів за одного кидання дорівнює 0,5? Це навіть неможливо уявити. Цікавіше поставити питання про кількість випадання орлів за заданої кількості кидків.
Іншими словами, дослідника часто цікавить ймовірність настання деякої кількості успішних подій. Це може бути кількість бракованих виробів у партії, що перевіряється (1- бракована, 0 - придатна) або кількість одужань (1 - здоровий, 0 - хворий) і т.д. Кількість таких «успіхів» дорівнюватиме сумі всіх значень змінної X, тобто. кількості поодиноких результатів.
Випадкова величина Bназивається біномною і набуває значення від 0 до n(при B= 0 - всі деталі придатні, при B = n- Усі деталі браковані). Передбачається, що всі значення xнезалежні між собою. Розглянемо основні характеристики біномної змінної, тобто встановимо її математичне очікування, дисперсію та розподіл.
Маточка біноміальної змінної отримати дуже легко. Математичне очікування суми величин є сума математичних очікувань кожної величини, що складається, а воно у всіх однакове, тому:
Наприклад, математичне очікування кількості орлів, що випали, при 100 підкиданнях дорівнює 100 × 0,5 = 50.
Тепер виведемо формулу дисперсії біноміальної змінної. Дисперсія суми незалежних випадкових величин є сумою дисперсій. Звідси
Стандартне відхилення, відповідно
Для 100 підкидань монети стандартне відхилення кількості орлів дорівнює
І, нарешті, розглянемо розподіл биномиальной величини, тобто. ймовірності того, що випадкова величина Bприйматиме різні значення k, де 0≤ k ≤n. Для монети це завдання може звучати так: якою є ймовірність випадання 40 орлів при 100 кидках?
Щоб зрозуміти метод розрахунку, уявімо, що монета підкидається лише 4 рази. Кожного разу може випасти кожна зі сторін. Ми запитуємо: яка ймовірність випадання 2 орлів з 4 кидків. Кожен кидок незалежний один від одного. Отже, ймовірність випадання будь-якої комбінації дорівнюватиме добутку ймовірностей заданого результату для кожного окремого кидка. Нехай О – це орел, Р – решка. Тоді, наприклад, одна з комбінацій, що влаштовують нас, може виглядати як ООРР, тобто:

Імовірність такої комбінації дорівнює добутку двох ймовірностей випадання орла та ще двох ймовірностей не випадання орла (зворотна подія, що розраховується як 1 - p), тобто. 0,5×0,5×(1-0,5)×(1-0,5)=0,0625. Така ймовірність однієї з комбінацій, що влаштовують нас. Але ж питання стояло про загальну кількість орлів, а не про якийсь певний порядок. Тоді потрібно скласти ймовірності всіх комбінацій, у яких є рівно 2 орла. Зрозуміло, всі вони однакові (від зміни місць множників твір не змінюється). Тому потрібно обчислити їх кількість, а потім помножити на ймовірність будь-якої комбінації. Підрахуємо всі варіанти поєднань із 4 кидків по 2 орли: РРОО, РОРО, РООР, ОРРО, ОРОР, ООРР. Усього 6 варіантів.

Отже, шукана можливість випадання 2 орлів після 4 кидків дорівнює 6×0,0625=0,375.
Однак підрахунок подібним чином стомливий. Вже для 10 монет шляхом перебору отримати загальну кількість варіантів буде дуже складно. Тому розумні людидавно винайшли формулу, за допомогою якої розраховують кількість різних поєднань з nелементів по k, де n– загальна кількість елементів, k- Кількість елементів, варіанти розташування яких і підраховуються. Формула поєднання з nелементів по kтака:
![]()
Подібні речі відбуваються у розділі комбінаторики. Усіх охочих підтягнути знання відправляю туди. Звідси, до речі, і назва біномного розподілу (формула вище є коефіцієнтом розкладання бінома Ньютона).
Формулу для визначення ймовірності легко узагальнити на будь-яку кількість nі k. У результаті формула біномного розподілу має такий вигляд.
Кількість відповідних за умов комбінацій помножити на ймовірність однієї з них.
Для практичного використання досить просто знати формулу біномного розподілу. А можна навіть не знати – нижче показано, як визначити ймовірність за допомогою Excel. Але краще все-таки знати.
Розрахуємо за цією формулою можливість випадання 40 орлів при 100 кидках:
Або лише 1,08%. Для порівняння, ймовірність настання математичного очікування цього експерименту, тобто 50 орлів, дорівнює 7,96%. Максимальна ймовірність біноміальної величини належить значенню, що відповідає математичному очікуванню.
Розрахунок ймовірностей біномного розподілу в Excel
Якщо використовувати тільки папір та калькулятор, то розрахунки за формулою біномного розподілу, незважаючи на відсутність інтегралів, даються досить важко. Наприклад значення 100! – має понад 150 знаків. Раніше, та й зараз, для обчислення подібних величин використовували наближені формули. На даний момент доцільно використовувати спеціальне програмне забезпечення, типу MS Excel. Таким чином, будь-який користувач (навіть гуманітарій за освітою) може обчислити ймовірність значення біноміально розподіленої випадкової величини.
Для закріплення матеріалу задіємо Excel поки як звичайний калькулятор, тобто. зробимо поетапне обчислення за формулою біномного розподілу. Розрахуємо, наприклад, можливість випадання 50 орлів. Нижче наведено картинку з етапами обчислень та кінцевим результатом.

Як видно, проміжні результати мають такий масштаб, що не поміщаються в комірку, хоча скрізь і використовуються прості функціїтипу: ФАКТР (обчислення факторіалу), СТУПЕНЬ (зведення числа до ступеня), а також оператори множення та поділу. Понад те, цей розрахунок досить громіздкий, у разі випадковий перестав бути компактним, т.к. задіяно багато осередків. Та й розібратися з ходу важкувато.
Загалом у Excel передбачено готову функцію для обчислення ймовірностей біномного розподілу. Функція називається БІНОМ.РАСП.

Число успіхів – кількість успішних випробувань. В нас їх 50.
Число випробувань - Кількість кидків: 100 разів.
Ймовірність успіху - Імовірність випадання орла при одному підкиданні 0,5.
Інтегральна - Вказується або 1, або 0. Якщо 0, то розрахується ймовірність P(B=k); якщо 1, то розрахується функція біномного розподілу, тобто. сума всіх ймовірностей від B=0до B=kвключно.
Натискаємо ОК і отримуємо той самий результат, що й вище, тільки все розрахувалося однією функцією.

Дуже зручно. Для експерименту замість останнього параметра 0 поставимо 1. Отримаємо 0,5398. Це означає, що при 100 підкидання монети ймовірність випадання орлів у кількості від 0 до 50 дорівнює майже 54%. А спочатку щось здавалося, що має бути 50%. Загалом розрахунки проводяться легко і швидко.
Справжній аналітик повинен розуміти, як поводиться функція (який її розподіл), тому зробимо розрахунок ймовірностей для всіх значень від 0 до 100. Тобто поставимо питання: яка ймовірність, що не випаде жодного орла, що випаде 1 орел, 2, 3 , 50, 90 або 100. Розрахунок наведено у наступній картинці. Синя лінія – саме біноміальний розподіл, червона точка – ймовірність для певної кількості успіхів k.

Хтось може запитати, а чи не схожий на біноміальний розподіл на… Так, дуже схоже. Ще Муавр (1733 р.) говорив, що біноміальний розподіл при великих вибірках наближається до (не знаю, як це тоді називалося), але його ніхто не слухав. Тільки Гаус, а потім і Лаплас через 60-70 років знову відкрили та ретельно вивчили нормальний законрозподілу. На графіці вище добре видно, що максимальна ймовірність посідає математичне очікування, а в міру відхилення від нього, різко знижується. Так само, як і у нормального закону.
Біноміальний розподіл має великий практичне значеннязустрічається досить часто. За допомогою Excel розрахунки проводяться легко та швидко.
Розглянемо здійснення схеми Бернуллі, тобто. проводиться серія повторних незалежних випробувань, у кожному з яких дана подія А має одну і ту ж ймовірність, яка не залежить від номера випробування. І для кожного випробування є лише два результати:
1) подія А – успіх;
2) подія – неуспіх,
з постійними ймовірностями
Введемо до розгляду дискретну випадкову величину Х - «число появи події А при пвипробуваннях» і знайдемо закон розподілу цієї випадкової величини. Величина Х може набувати значення
Ймовірність ![]() того, що випадкову величину Х набуде значення x kзнаходиться за формулою Бернуллі
того, що випадкову величину Х набуде значення x kзнаходиться за формулою Бернуллі
Закон розподілу дискретної випадкової величини, який визначається формулою Бернуллі (1), називається біномним законом розподілу. Постійні п і р (q=1-p), що входять у формулу (1) називаються параметрами біномного розподілу.
Назва «біноміальний розподіл» пов'язана з тим, що права частина рівності (1) це загальний член розкладання бінома Ньютона, тобто.
(2)
А оскільки p+q=1, то права частина рівності (2) дорівнює 1
Це означає, що
 (4)
(4)
У рівності (3) перший член q nу правій частині означає ймовірність того, що в пвипробуваннях подія А не з'явиться жодного разу, другий член ![]() ймовірність того, що подія А з'явиться один раз, третій член - ймовірність, що подія А з'явиться двічі і нарешті останній член р п- ймовірність того, що подія А з'явиться рівно празів.
ймовірність того, що подія А з'явиться один раз, третій член - ймовірність, що подія А з'явиться двічі і нарешті останній член р п- ймовірність того, що подія А з'явиться рівно празів.
Біноміальний закон розподілу дискретної випадкової величини подають у вигляді таблиці:
| Х | 0 | 1 | … | k | … | n |
| Р | q n | … | … | р п |
Основні числові характеристикибіномного розподілу:
1) математичне очікування ![]() (5)
(5)
2) дисперсія ![]() (6)
(6)
3) середнє квадратичне відхилення ![]() (7)
(7)
4) найімовірніше число поява події k 0- це число якому при заданому пвідповідає максимальна біномна ймовірність
При заданих пі рце число визначається нерівностями
![]() (8)
(8)
якщо число пр+рне є цілим, то k 0дорівнює цілій частині цього числа, якщо ж пр+р- ціле число, то k 0має два значення
Біноміальний закон розподілу ймовірностей застосовується в теорії стрільби, теорії та практики статистичного контролю якості продукції, теорії масового обслуговування, теорії надійності і т.д. Цей закон може застосовуватися у всіх випадках, коли є послідовність незалежних випробувань.
Приклад 1:Перевіркою якості встановлено, що з кожних 100 приладів немає дефектів 90 штук у середньому. Скласти біноміальний закон розподілу ймовірностей числа якісних приладів із придбаних навмання 4.
Рішення:Подія А - поява якого перевіряється це - «придбаний навмання прилад якісний». За умовою завдання основні параметри біномного розподілу:
Випадкова величина Х - число якісних приладів із взятих 4, означає значення Х -Знайдемо ймовірність значень Х за формулою (1):

Таким чином, закон розподілу величини Х - кількість якісних приладів із взятих 4:
| Х | 0 | 1 | 2 | 3 | 4 |
| Р | 0,0001 | 0,0036 | 0,0486 | 0,2916 | 0,6561 |
Для перевірки правильності побудови розподілу перевіримо, чому дорівнює сума ймовірностей
Відповідь:Закон розподілу
| Х | 0 | 1 | 2 | 3 | 4 |
| Р | 0,0001 | 0,0036 | 0,0486 | 0,2916 | 0,6561 |
Приклад 2:Застосовуваний метод лікування призводить до одужання у 95% випадків. П'ятеро хворих застосовували цей метод. Знайти найбільш імовірне число одужали, а так само числові характеристики випадкової величини Х - число одужали з 5 хворих, що застосовували даний метод.
Біноміальний розподіл - один з найважливіших розподілів ймовірностей випадкової величини, що дискретно змінюється. Біноміальним розподілом називається розподіл ймовірностей числа mнастання події Ав nвзаємно незалежні спостереження. Часто подія Аназивають "успіхом" спостереження, а протилежна йому подія - "неуспіхом", але це позначення дуже умовне.
Умови біномного розподілу:
- загалом проведено nвипробувань, у яких подія Аможе наступити чи наступити;
- подія Ау кожному з випробувань може наступити з однією і тією самою ймовірністю p;
- випробування є взаємно незалежними.
Імовірність того, що в nвипробуваннях подія Анастане саме mраз, можна обчислити за формулою Бернуллі:
![]()
де p- ймовірність настання події А;
q = 1 - p- Імовірність настання протилежної події.
Розберемося, чому біномний розподіл описаним вище чином пов'язаний з формулою Бернуллі . Подія - кількість успіхів при nвипробуваннях розпадається на ряд варіантів, у кожному з яких успіх досягається в mвипробуваннях, а неуспіх - у n - mвипробуваннях. Розглянемо один із таких варіантів - B1 . За правилом складання ймовірностей примножуємо ймовірності протилежних подій:
![]() ,
,
а якщо позначимо q = 1 - p, то
![]() .
.
Таку ж ймовірність матиме будь-який інший варіант, у якому mуспіхів та n - mнеуспіхів. Число таких варіантів дорівнює - числу способів, якими можна з nвипробувань отримати mуспіхів.
Сума ймовірностей усіх mчисел настання події А(чисел від 0 до n) дорівнює одиниці:

де кожен доданок являє собою доданок бінома Ньютона. Тому розподіл, що розглядається, і називається біноміальним розподілом.
Насправді часто необхідно обчислювати ймовірності " трохи більше mуспіхів у nвипробуваннях" або "не менше mуспіхів у nвипробуваннях". Для цього використовуються наступні формули.
Інтегральну функцію, тобто ймовірність F(m) того, що в nспостереженнях подія Анастане не більше mраз, Можна обчислити за формулою:
У свою чергу ймовірність F(≥m) того, що в nспостереженнях подія Анастане не менше mраз, обчислюється за такою формулою:
Іноді буває зручніше обчислювати ймовірність того, що в nспостереженнях подія Анастане не більше mраз, через ймовірність протилежної події:
![]() .
.
Який із формул користуватися, залежить від того, в якій із них сума містить менше доданків.
Характеристики біномного розподілу обчислюються за такими формулами .
Математичне очікування: .
Дисперсія: .
Середньоквадратичне відхилення: .
Біноміальний розподіл та розрахунки в MS Excel
Імовірність біномного розподілу P n ( m) та значення інтегральної функції F(m) можна обчислити за допомогою функції MS Excel БІНОМ.РАСП. Вікно для відповідного розрахунку показано нижче (для збільшення натиснути лівою кнопкою миші).

MS Excel вимагає ввести такі дані:
- кількість успіхів;
- кількість випробувань;
- ймовірність успіху;
- інтегральна - логічне значення: 0 - якщо потрібно вирахувати ймовірність P n ( m) і 1 - якщо ймовірність F(m).
приклад 1.Менеджер фірми узагальнив інформацію про кількість проданих протягом останніх 100 днів фотокамер. У таблиці узагальнено інформацію та розраховано ймовірність того, що в день буде продано певну кількість фотокамер.
День завершено із прибутком, якщо продано 13 або більше фотокамер. Імовірність, що день буде відпрацьовано із прибутком:
![]()
Імовірність того, що день буде відпрацьовано без прибутку:
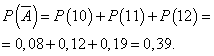
Нехай ймовірність того, що день відпрацьований з прибутком, є постійною і дорівнює 0,61 і кількість проданих в день фотокамер не залежить від дня. Тоді можна використовувати біномний розподіл, де подія А- день буде відпрацьовано із прибутком, - без прибутку.
Імовірність того, що з 6 днів усі будуть відпрацьовані із прибутком:
![]() .
.
Той самий результат отримаємо, використовуючи функцію MS Excel БІНОМ.РАСП (значення інтегральної величини - 0):
P 6 (6 ) = БІНОМ.РАСП(6; 6; 0,61; 0) = 0,052.
Імовірність того, що з 6 днів 4 і більше днів будуть відпрацьовані із прибутком:
де ![]() ,
,
![]() ,
,
Використовуючи функцію MS Excel БІНОМ.РАСП, обчислимо ймовірність того, що з 6 днів не більше 3 днів буде завершено з прибутком (значення інтегральної величини - 1):
P 6 (≤3 ) = БІНОМ.РАСП(3; 6; 0,61; 1) = 0,435.
Імовірність того, що з 6 днів усі будуть відпрацьовані зі збитками:
![]() ,
,
Той самий показник обчислимо, використовуючи функцію MS Excel БІНОМ.РАСП:
P 6 (0 ) = БІНОМ.РАСП(0; 6; 0,61; 0) = 0,0035.
Вирішити завдання самостійно, а потім переглянути рішення
приклад 2.В урні 2 білі кулі та 3 чорні. З урни виймають кулю, встановлюють колір і кладуть назад. Спробу повторюють 5 разів. Число появи білих куль - дискретна випадкова величина X, розподілена за біноміальним законом. Скласти закон розподілу випадкової величини. Визначити моду, математичне очікування та дисперсію.
Продовжуємо вирішувати завдання разом
приклад 3.З кур'єрської служби вирушили на об'єкти n= 5 кур'єрів. Кожен кур'єр з ймовірністю p= 0,3 незалежно від інших спізнюється об'єкт. Дискретна випадкова величина X- Число запізнілих кур'єрів. Побудувати низку розподілу це випадкової величини. Знайти її математичне очікування, дисперсію, середнє відхилення. Знайти ймовірність того, що на об'єкти запізняться щонайменше два кур'єри.